A block of steel of size 5cm×5cm×5cm is weighed in water. If the relative density of steel is 7. its apparent weight is:
6×5×5×5gf
4×4×4×7gf
5×5×5×7gf
4×4×4×6gf
The correct Answer is:A
To find the apparent weight of a block of steel when submerged in water, we can follow these steps:
Step 1: Calculate the Volume of the Steel Block
The volume V of the steel block can be calculated using the formula for the volume of a cube:
V=side3
Given that the size of the block is 5cm×5cm×5cm:
V=5cm×5cm×5cm=125cm3
Step 2: Calculate the Weight of the Steel Block in Air
The weight W of the steel block in air is given by:
W=m⋅g
where m is the mass of the block and g is the acceleration due to gravity. The mass can be calculated using the density of steel and the volume:
m=ρ⋅V
Given that the relative density of steel is 7, we can express the density of steel ρ in terms of the density of water ρw:
ρ=7⋅ρw
Substituting this into the mass equation:
m=7⋅ρw⋅V
Thus, the weight in air becomes:
W=7⋅ρw⋅V⋅g
Step 3: Calculate the Buoyant Force
The buoyant force Fb acting on the block when submerged in water is given by Archimedes' principle:
Fb=ρw⋅V⋅g
Step 4: Calculate the Apparent Weight
The apparent weight W′ of the block when submerged in water can be calculated using the formula:
W′=W−Fb
Substituting the expressions for W and Fb:
W′=(7⋅ρw⋅V⋅g)−(ρw⋅V⋅g)
Factoring out ρw⋅V⋅g:
W′=(ρw⋅V⋅g)⋅(7−1)=6⋅ρw⋅V⋅g
Step 5: Substitute the Volume and Density of Water
Now, substituting the volume V=125cm3 and using ρw (density of water) which is approximately 1g/cm3:
W′=6⋅(1g/cm3)⋅(125cm3)⋅g
W′=750g⋅g
Final Result
Thus, the apparent weight of the steel block when submerged in water is:
W′=750gf
The volume V of the steel block can be calculated using the formula for the volume of a cube:
V=side3
Given that the size of the block is 5cm×5cm×5cm:
V=5cm×5cm×5cm=125cm3
The weight W of the steel block in air is given by:
W=m⋅g
where m is the mass of the block and g is the acceleration due to gravity. The mass can be calculated using the density of steel and the volume:
m=ρ⋅V
Given that the relative density of steel is 7, we can express the density of steel ρ in terms of the density of water ρw:
ρ=7⋅ρw
Substituting this into the mass equation:
m=7⋅ρw⋅V
Thus, the weight in air becomes:
W=7⋅ρw⋅V⋅g
The buoyant force Fb acting on the block when submerged in water is given by Archimedes' principle:
Fb=ρw⋅V⋅g
The apparent weight W′ of the block when submerged in water can be calculated using the formula:
W′=W−Fb
Substituting the expressions for W and Fb:
W′=(7⋅ρw⋅V⋅g)−(ρw⋅V⋅g)
Factoring out ρw⋅V⋅g:
W′=(ρw⋅V⋅g)⋅(7−1)=6⋅ρw⋅V⋅g
Now, substituting the volume V=125cm3 and using ρw (density of water) which is approximately 1g/cm3:
W′=6⋅(1g/cm3)⋅(125cm3)⋅g
W′=750g⋅g
Thus, the apparent weight of the steel block when submerged in water is:
W′=750gf
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.32
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.33
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.30
Explore 9 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 21 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
A wooden block of dimensions 10cm×20cm×50cm weighs 6-5 kg Calculate the density of the block.
View SolutionA force of 5×103 N is applied tangentially to the upper face of a cubical block of steel of side 30 cm. Find the displacement of the upper face relative to the lower one, and the angle of shear. The shear modulus of steel is 8.3×1010 pa.
View Solution
Knowledge Check
A block of steel of size 5cm×5cm×5 cm is weighed in water. If the relative density of steel is
A6×5×5×5gB4×4×4×7gC5×5×5×7gD4×4×4×6gIf a block of iron (density 5gcm−3) is size 5 cm xx 5 cm xx 5 cm was weight while completely submerged in water, what would be the apperent weight ?
A5xx5xx5xx5 gfB4xx4xx4xx5 gfC3xx5xx5xx5 gfD4xx5xx5xx5 gfA steel block having an internal cavity weighs 234g in air and 197g in water. If the density of steel is 7.8gcm−3 then the volume of the cavity is
A5cm3B7cm3C9cm3D11cm3
A wall of dimensions 24m×5m×0.25m is to be constructed using bricks of dimensions 25cm×12.5cm×7.5cm. Find the number of bricks requires if 5% of the wall is occupied by cement and mixture.
View SolutionA brick with dimensions of 20cm× 10cm× 5cm has a weight 500g wt. Calculate the pressure exerted by it when it rests on different faces. In which case is the pressure exerted the greatest?
View SolutionA wire is suspended vertically from a rigid support. When loaded with a steel weight in air, the wire extends by 16cm. When the weight is completely immersed in Water, the extension is reduced to 14cm. The relative density of the material of the weight is
View SolutionA rectangular block is 5cm×5cm×10cm in size. The block is floating in water with 5 cm side vertical. If it floats with 10 cm side vertical, what change will occur in the level of water?
View SolutionIn the given figure from a cuboidal solid metallic block of dimensions 15cm×10cm×5cm a cylindrical hole of diamter 7 cm is drilled out . Find the suface area of the remaining block .
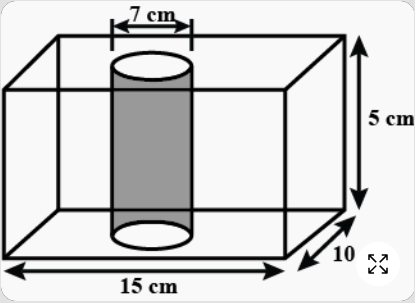
View Solution
