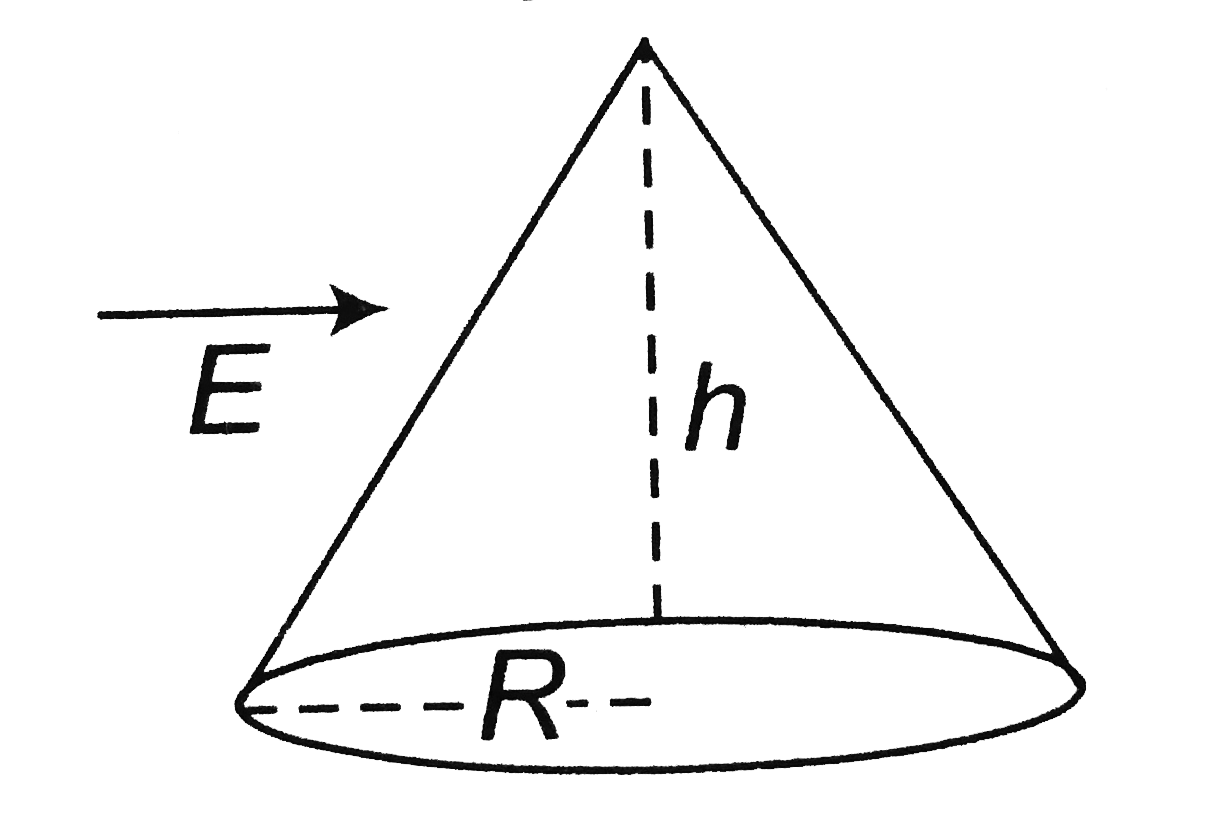
A conic surface is placed in a uniform electric field E as shown in figure. Such that the field is perpendicular to the surface on the side AB. The base of the cone is of radius R, and the height of the cone is h. The angle of the cone is $θ$ .

Find the magnitude of the flux that enters the cone's curved surface from the left side. Do not count the outgoing flux $(θ < 45^{\circ})$ .

A

$E R [h cos θ + π (R / 2) sin θ]$

B

$E R [h cos θ + π R / 2 sin θ]$

C

$E R [h cos θ + π R sin θ]$

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

a. Flux entering the cone from side $A B$ will ultimately also pass
through areas $A_{1}$ and $A_{2}$ . So,
$ϕ = E A_{1} cos θ + E A_{2} cos (90 - θ)$
$= E (\frac{1}{2} 2 R h cos θ + \frac{π}{2} R^{2} sin θ)$
$= E R [h cos θ + π (R / 2) sin θ]$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A cone lies in a uniform electric field $E$ as shown in figure. The electric flux entering the cone is

A $E π R^{2}$
B $E R h$
C $\frac{E h R}{2}$
D $E h^{2}$
Question 2 - Select One
The curved surface area of the cone of radius 5 cm and height 12 cm is
A $60 π c m^{2}$
B $65 π c m^{2}$
C $300 π c m^{2}$
D $325 π c m^{2}$
Question 3 - Select One
If the curved surface area of a cone is thrice that of another cone and slant height of the second cone is thrice that of the first, find the ratio of the area of their base.
A $81 : 1$
B $9 : 1$
C $3 : 1$
D $27 : 1$

CENGAGE PHYSICS-ELECTRIC FLUX AND GAUSS LAW-Single Correct

Home
Ask Doubt
Profile