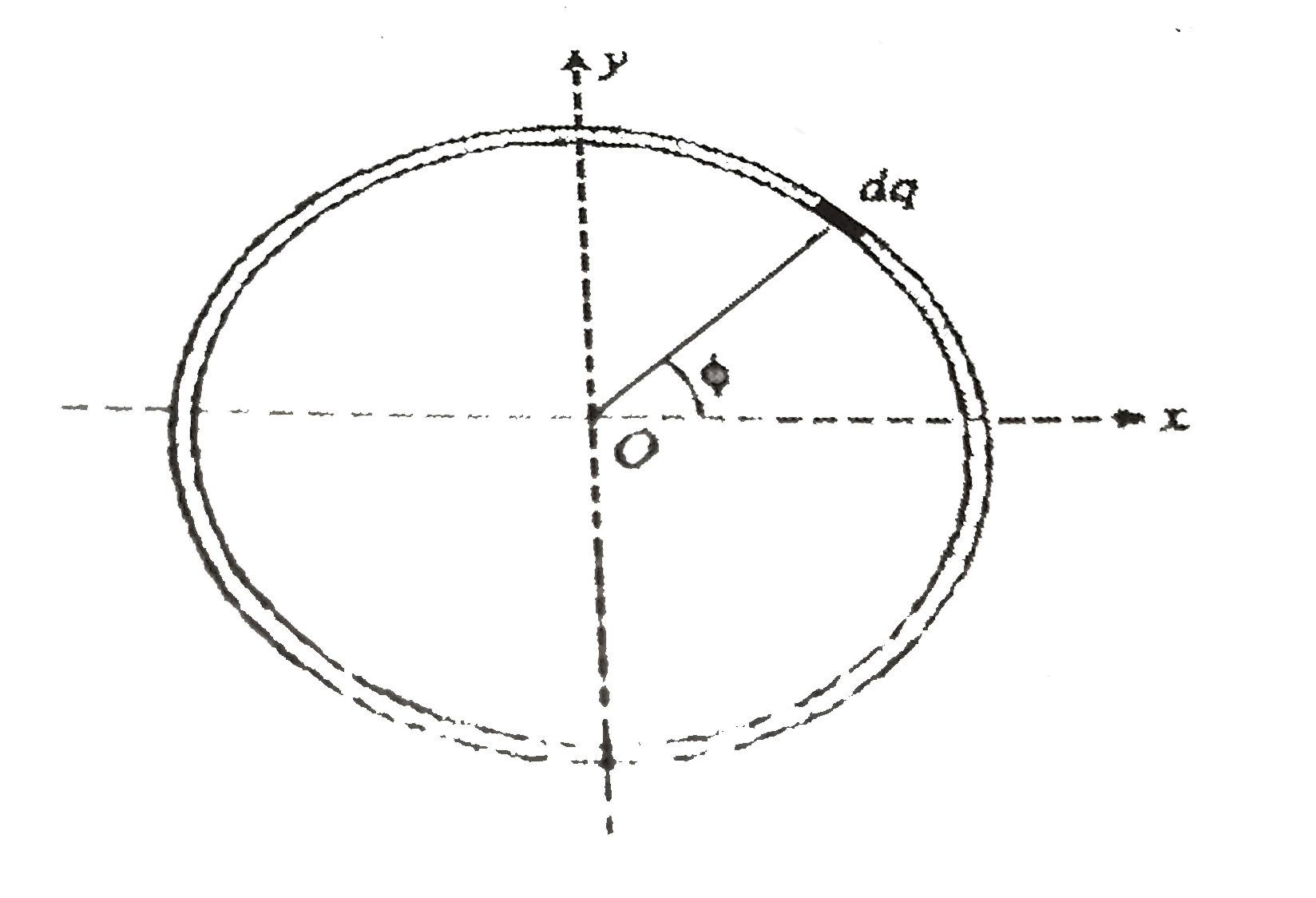
A thin nonconducting ring of radius $R$ has a linear charge density $λ = λ_{0} cos φ$ , where $λ_{0}$ is a constant , $ϕ$ is the azimutahl angle. Find the magnitude of the electric field strength
(a) at the centre of the ring ,
(b) on the axis of the ring as a function of the distance $x$ from its centre. Investegation the obtained function at $x > > R$ .

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem, we will break it down into two parts:
Part (a): Electric Field at the Center of the Ring
1. Understanding the Charge Distribution: The linear charge density is given by $λ (φ) = λ_{0} cos φ$ . This means that the charge is distributed non-uniformly along the ring.
2. Consider a Small Element of Charge: Take a small element of the ring $d φ$ at an angle $φ$ . The charge $d q$ on this element is:
$d q = λ (φ) R d φ = λ_{0} R cos φ d φ$
3. Electric Field Contribution: The electric field $d E$ due to this charge at the center of the ring will have both x and y components. However, due to symmetry, the y-components will cancel out when integrating over the entire ring.
4. Calculating the x-component: The x-component of the electric field due to $d q$ at the center is:
$d E_{x} = d E cos φ$
where $d E = \frac{k d q}{R^{2}} = \frac{k λ_{0} R cos φ d φ}{R^{2}} = \frac{k λ_{0} cos φ}{R} d φ$ .
5. Integrating Over the Ring: The total electric field at the center is:
$E_{x} = \int_{0}^{2 π} d E_{x} = \int_{0}^{2 π} \frac{k λ_{0} cos φ}{R} d φ$
The integral of $cos φ$ over a complete cycle (0 to $2 π$ ) is zero:
$E_{x} = 0$
6. Conclusion for Part (a): Therefore, the electric field at the center of the ring is:
$E = 0$
Part (b): Electric Field on the Axis of the Ring
1. Setting Up the Geometry: Consider a point on the axis of the ring at a distance $x$ from the center. The electric field due to a small charge element $d q$ at this point will have a component along the axis.
2. Electric Field Contribution: The distance from the charge element to the point on the axis is given by:
$r = \sqrt{R^{2} + x^{2}}$
The electric field due to $d q$ at this point is:
$d E = \frac{k d q}{r^{2}} = \frac{k λ_{0} R cos φ d φ}{R^{2} + x^{2}}$
3. Finding the z-component: The z-component of this electric field is:
$d E_{z} = d E \cdot \frac{x}{r} = \frac{k λ_{0} R cos φ d φ}{R^{2} + x^{2}} \cdot \frac{x}{\sqrt{R^{2} + x^{2}}}$
4. Integrating Over the Ring: The total electric field along the z-axis is:
$E_{z} = \int_{0}^{2 π} d E_{z} = \int_{0}^{2 π} \frac{k λ_{0} R cos φ x}{(R^{2} + x^{2})^{3 / 2}} d φ$
Again, the integral of $cos φ$ over a complete cycle is zero:
$E_{z} = 0$
5. Conclusion for Part (b): Therefore, the electric field on the axis of the ring is also:
$E = 0$
Investigating the Function at $x ≫ R$
1. Behavior of the Electric Field: Since both components of the electric field are zero regardless of the distance $x$ , the electric field remains zero even as $x$ becomes much larger than $R$ .
Summary of Results
- (a) The electric field at the center of the ring is $E = 0$ .
- (b) The electric field on the axis of the ring is also $E = 0$ , and this holds true for $x ≫ R$ .

Updated on:7/8/2024

A thin non-conducting ring of radius $R$ has a linear charge density $λ = λ_{0} cos θ$ , where $θ$ is measured as shown. The total electric dipole moment of the charge distribution is

A $R^{2} λ_{0}$
B $2 π R^{2} λ_{0}$
C $\frac{π R^{2} λ_{0}}{2}$
D $π R^{2} λ_{0}$
A half ring of radius $r$ has a linear charge density $λ$ .The potential at the centre of the half ring is
A $\frac{λ}{4 ε o {ln}_{0}}$
B $\frac{λ}{4 π^{2} ε_{0} r}$
C $\frac{λ}{4 π ε_{0} r}$
D $\frac{λ}{4 π ε_{0} r^{2}}$
The linear charge density on a ring of radius R is $λ = λ_{0} sin (θ)$ where $λ_{0}$ is a constant and $θ$ is angle of radius vector of any point on the ring with x-axis. The electric potential at centre of ring is

A0
B $\frac{λ_{0}}{\in_{0}}$
C $\frac{λ_{0}}{π \in_{0}}$
D $\frac{λ_{0}}{2 π \in_{0}}$