A rod with linear charge density λ is bent in the shap of circular ring. The electric potential at the centre of the circular ring is
λε0
λ2ε0
λε0
2λε0
The correct Answer is:2
σ=QA
Topper's Solved these Questions
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:NCERT based Question
Explore 14 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Level V
Explore 93 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Level 2
Explore 10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:ADDITIONAL PROBLEMS
Explore 14 Videos
- EXPERIMENTAL PHYSICSBook:NARAYNAChapter:EXPERIMENTAL PHYSICSExercise:Comprehension type
Explore 6 Videos
Similar Questions
Consider a circular ring of radius r, uniformly charged with linear charge density λ. Find the electric potential aty a point on the exis at a distance x from the centre of the ring. Using this expression for the potential, find the electric field at this point.
View SolutionA quarter ring of radius R is having uniform charge density λ. Find the electric field and potential at the centre of the ring.
View Solution
Knowledge Check
Two semicircular rings lying in same plane, of uniform linear charge density λ have radius r and 2r. They are joined using two straight uniformly charged wires of linear charge density λ and length r as shown in figure. The magnitude of electric field at common centre of semi circular rings is -
 A14πε03λ2rB14πε0λ2rC14πε02λrD14πε0λr
A14πε03λ2rB14πε0λ2rC14πε02λrD14πε0λrA semicircular ring of radius 0.5 m is uniformly charged with a total charge of 1.5×10−9 coul. The electric potential at the centre of this ring is :
A27 VB13.5 VC54 VD45.5 VAn infinitely long wire with linear charge density +λ is bent and the two parts are inclined at angle 30∘ as shown in fig, the electric field at point P is :
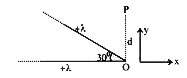 Aλ4π∈0d[(1+√3)ˆi+ˆj]Bλ4π∈0d[(1−√3)ˆi+2ˆj]Cλ4π∈0d[(1+√3)ˆi−2ˆj]Dλ4π∈0d[(1+√3)ˆi+2ˆj]
Aλ4π∈0d[(1+√3)ˆi+ˆj]Bλ4π∈0d[(1−√3)ˆi+2ˆj]Cλ4π∈0d[(1+√3)ˆi−2ˆj]Dλ4π∈0d[(1+√3)ˆi+2ˆj]
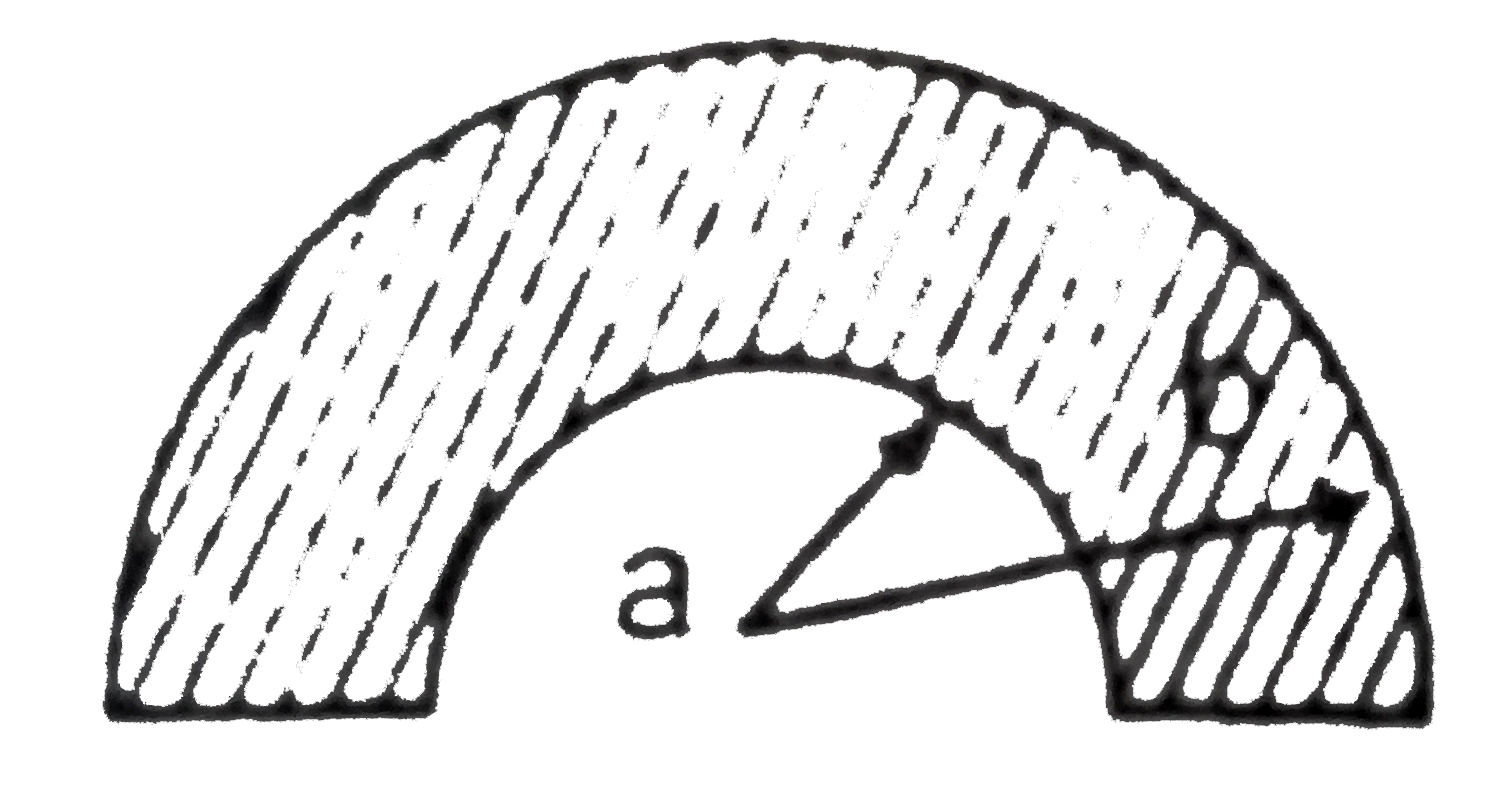
A non-conducting semi circular disc (as shown in figure) has a uniform surface charge density σ. The ratio of electric field to electric potential at the centre of the disc will be
View SolutionA charge Q is uniformly distributed only on the fourths portion of a ring of radius R. The elctric potential at centre of ring is
View SolutionA wire of mass m and length l is bent in the form of circular ring. The moment of inertia of the ring about its axis is
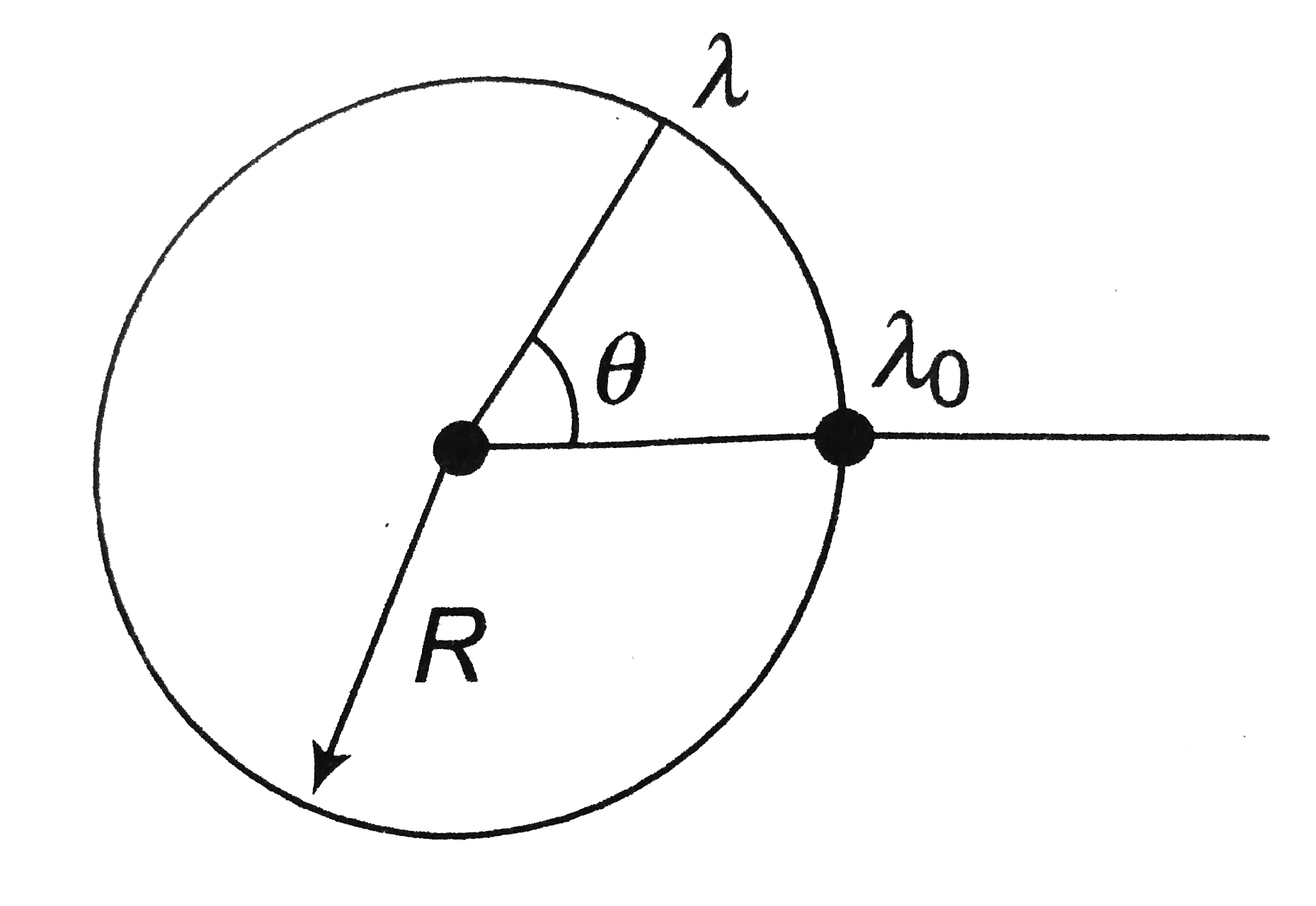
View SolutionA thin non-conducting ring of radius R has a linear charge density λ=λ0cosθ, where θ is measured as shown. The total electric dipole moment of the charge distribution is
View SolutionCharges q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
View Solution

