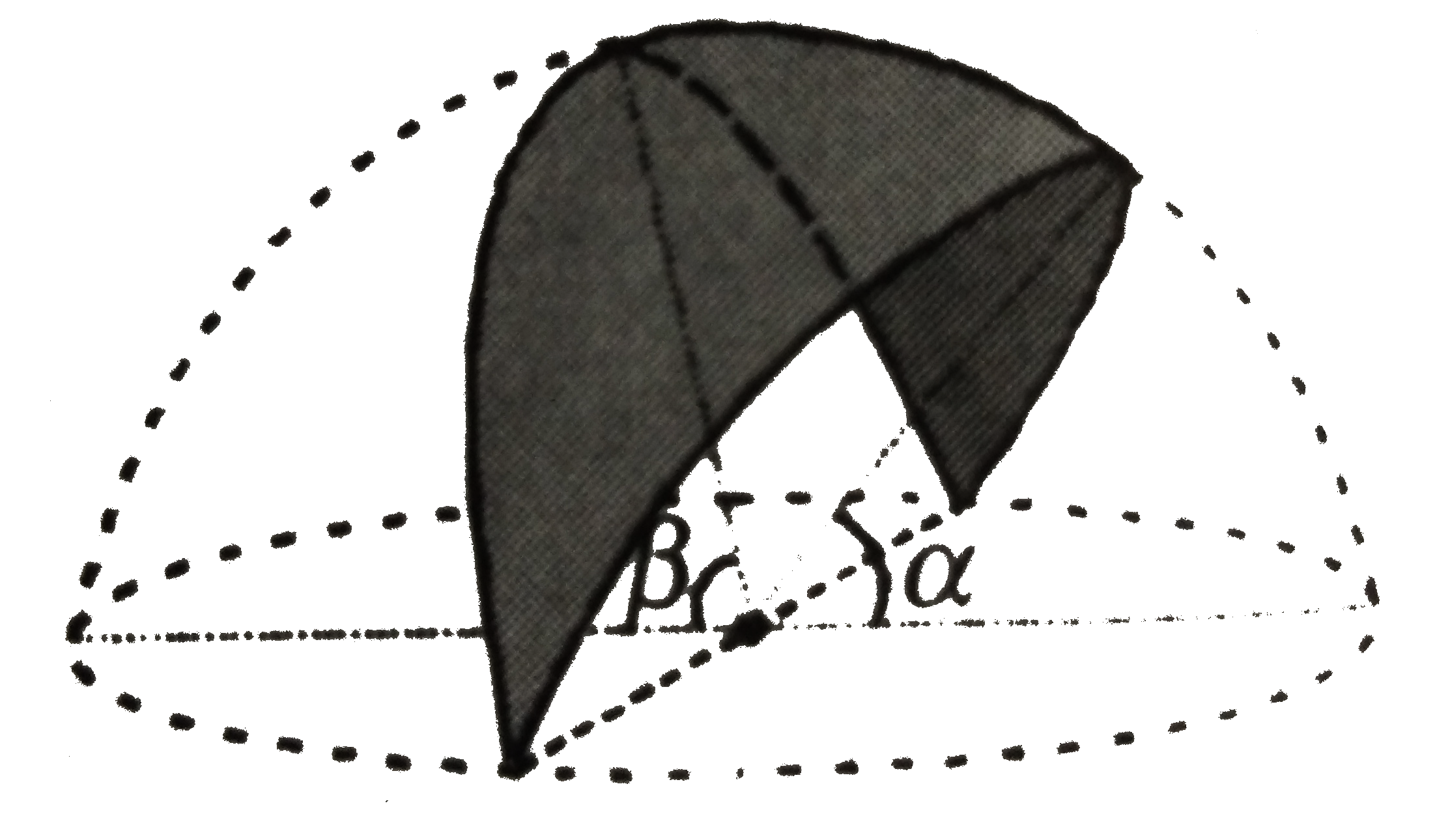
The electric field intensity at the center of a uniformly charged hemispherical shell is E0. Now two portions of the hemisphere are cut from either side, and the remaining portion is shown in fig. If α=β=π/3, then the electric field intensity at the center due to the remaining portion is
E03
E06
E02
E0

consider the whole hemispere as three portion if electric field due to one portion is E1 then 2E1sin30+E1=E0
2E1=E0
⇒E1=E02
Topper's Solved these Questions
Similar Questions
Knowledge Check
The expression for electric field intensity at a points outside uniformly charged thin plane sheet is (where, d is the distance of point from plane sheet)
Aindependent of dBdirectly proportional to √dCdirectly proportional to dDdirectly proportional to 1√dA circular ring of radius r carries a charge Q uniformly spread on it. A small length dl is cut off. Find the electric field at the centre due to the remaining wire.
AQ4πε0r2BQdl4π2ε0r3CQdl8π2ε0r2DQdl8π2ε0r3
Find the electric field due to an uniformly charged arc, at the center 'c'.

View SolutionElectric field at the centre of uniformly charge hemispherical shell of surface charge density σ is σnε0 then find the value of n.

View SolutionA long wire with a uniform charge density λ is bent in two configurations shown in fig. Determine the electric field intensity at point O.
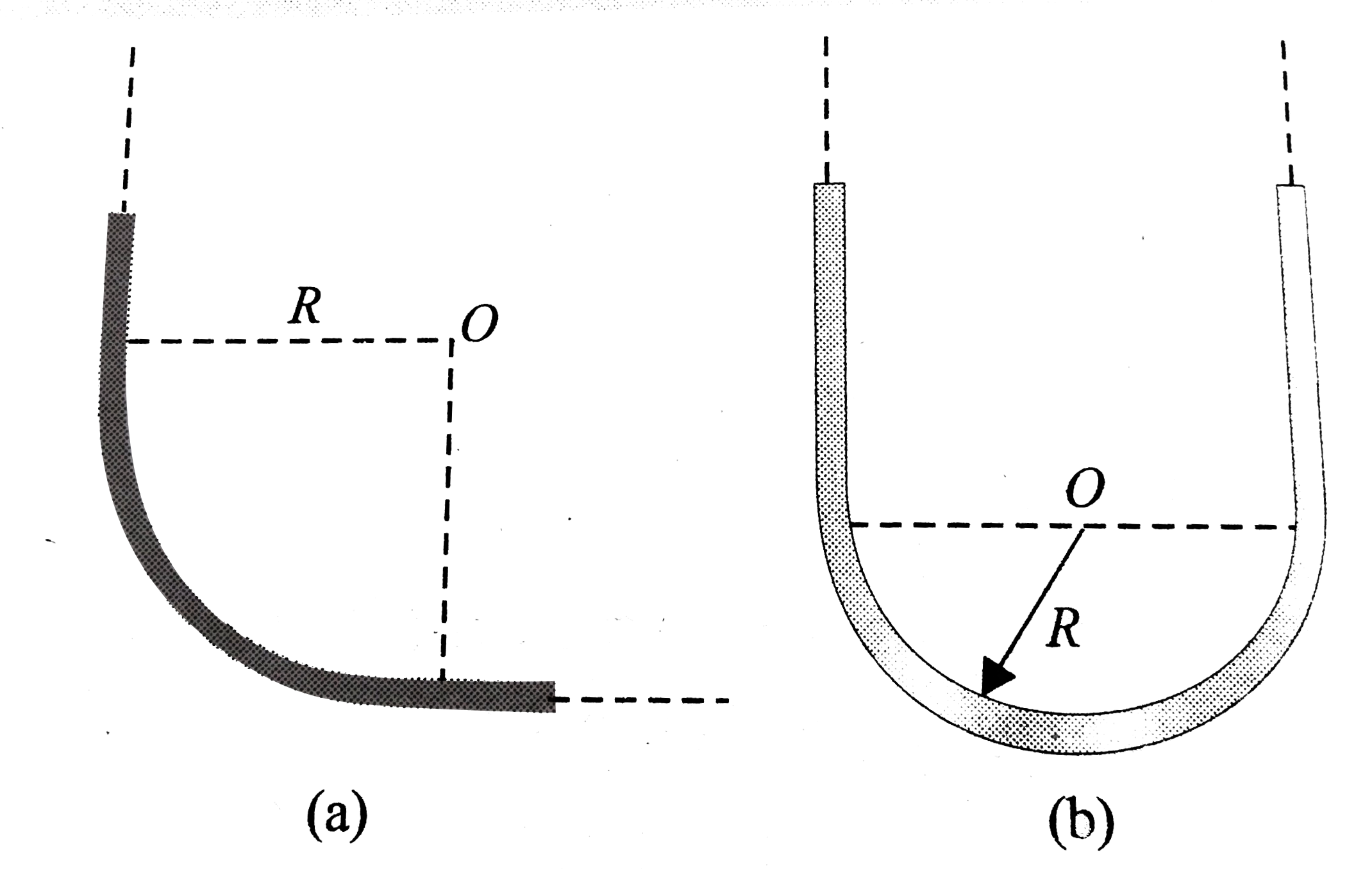
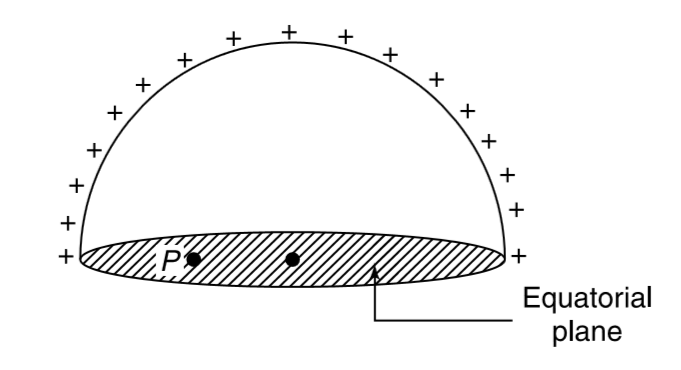
View SolutionConsider a uniformly charged hemispherical shell. What can you say about the direction of electric field at points on the equatorial plane. (e.g. point P)
View SolutionStatement 1:Electric field intensity at surface of uniformly charged spehrical shell is E if the shell is puncurted at a point then intensity at punctured point becomed E/2.
Statement 2:Electric field intensity due to spherical charge distribution can be found out by using GaussLaw.
View Solution" Electric field intensity due to a point charge " "q" ' at a distance 'r' from it is "
View Solution

