Two point charges having charge +Q, –q and mass M, m respectively are separated by a distance L. They are released from rest in a uniform electric field E. The electric field is parallel to line joining both the charges and is directed from negative to positive charge. For the separation between particles to remain constant, the value of L is
(K=14π∈0)
√(M+m)KQqE(qM+Qm)
√(M+m)KQqE(qm+QM)
√mMKQqE(qM+Qm)
√mMKQqE(QM+qm)
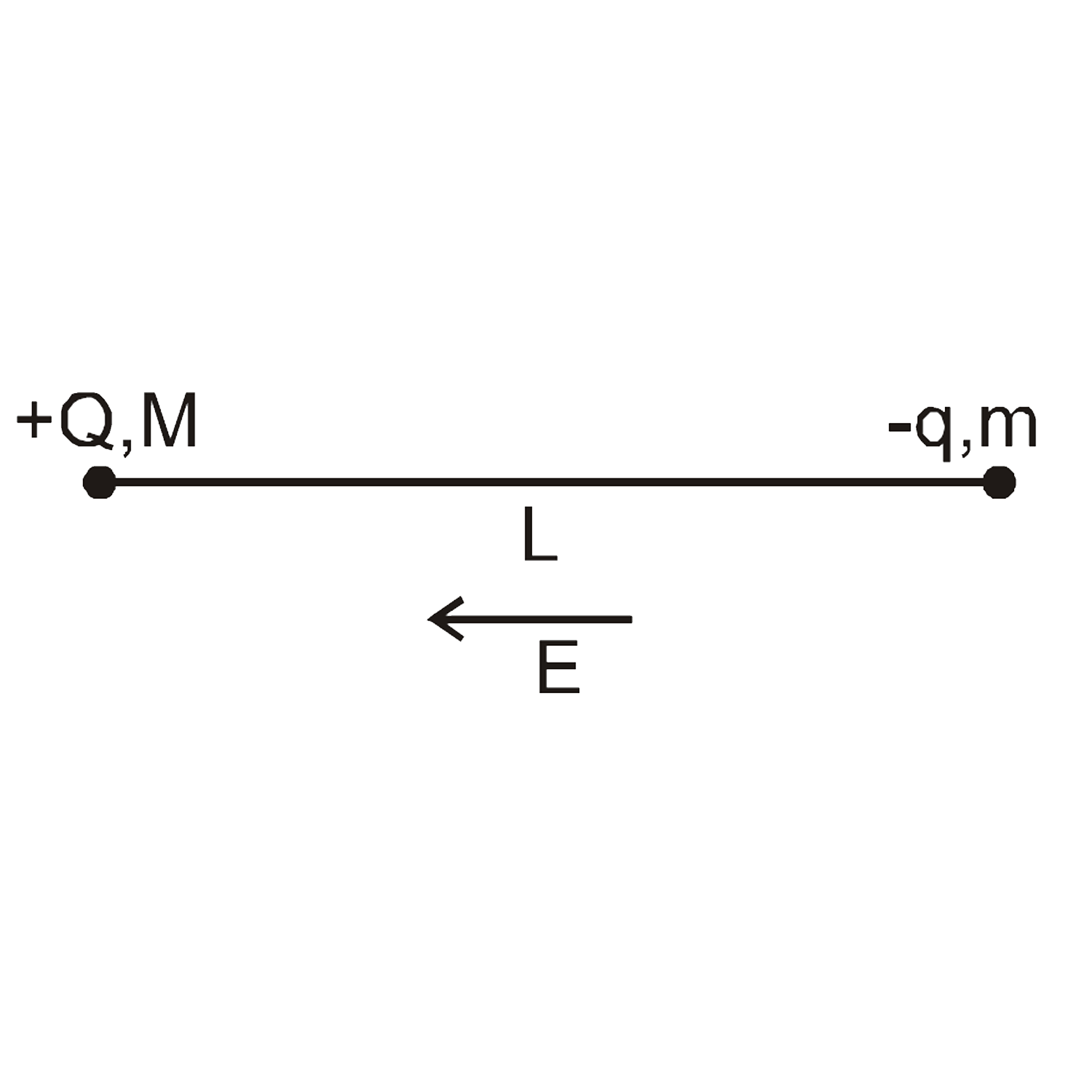
In order to maintain constant separation the particles must have the same acceleration assuming the system of both charges to accelerate towards left. Applying newton's second law.
QE=KQqL2=Ma .(i)
Undergiven condition the acceleration of both charges should be same and should also be equal to acceleration of centre of mass of both the charges.
Hence from equation (1) and (2) we get L=
⎷((M+m)KQqE(qM+Qm))
Topper's Solved these Questions
Similar Questions
A protons of mass m charge 2 e is released from rest in a uniform electric field of strength E .The time taken by it to travel a distance d in the field is..
View SolutionTwo point charges+ q and-q are placed at distanced apart. What are the points at which the resultant field is parallel to the line joining the two charges ?
View Solution
Knowledge Check
A positively charged particle is released from rest in a uniform electric field. The electric potential energy of the charge.
Aremains a constant because the electric field is uniform.Bincrease because the charge moves along the electric field.Cdecreases because the charge moves along the electric field.Ddecreases because the charge moves opposite to the electric field.A positively charged particle is released from rest in an uniform electric field. The electric potential energy of the charge
Aremains a constant because the electric field is uniform.Bincreases because the charge moves along the electric field.Cdecreases because the charge moves along the electric field.Ddecreases because the charge moves opposite to the electric field.A protons of mass m charge c is released form rest in a uniform electric field of strength E .The time taken by it to travel a distance d in the field is
A√2demEB√2dmEeC√2dEmeD√2dEedm
Two charged particle having masses in the ratio 2:3 and charges in the ratio 1:2 are released from rest in a uniform electric field.After a time 1 minute their K.E.will be in the ratio of
View SolutionA charge particle of mass m and charge q is released from rest in uniform electric field. Its graph between velocity (v) and distance travelled (x) will be :
View SolutionA charged particle of mass m and charge e is released from rest in an electric field E. If kinetic energy of particle after time t is Ek and linear momentum is p, then
View SolutionA : Electric field lines are continuous curves in free space.
R : Electric field lines start from negative charge and terminate at positive charge.
View SolutionAn electron of mass m and charge q is accelerated from rest in a uniform electric field of strength E. The velocity acquired by it as it travels a distance l is
View Solution

