An electron of mass m and charge q is accelerated from rest in a uniform electric field of strength E. The velocity acquired by it as it travels a distance l is
√2Eql/m
√2Eq/ml
√2Em/ql
√Eq/ml
The correct Answer is:A
To find the velocity acquired by an electron of mass m and charge q when it is accelerated from rest in a uniform electric field of strength E over a distance l, we can follow these steps:
1. Identify the Initial Conditions:
The electron starts from rest, so its initial velocity u=0.
2. Understand the Forces Acting on the Electron:
The force F acting on the electron due to the electric field is given by:
F=qE
where q is the charge of the electron and E is the strength of the electric field.
3. Calculate the Acceleration:
According to Newton's second law, the acceleration a of the electron can be calculated using:
a=Fm=qEm
where m is the mass of the electron.
4. Use the Kinematic Equation:
We can use the kinematic equation that relates acceleration, distance, and velocity:
v2=u2+2as
Since the initial velocity u=0, this simplifies to:
v2=2as
5. Substitute the Values:
Substitute a=qEm and s=l (the distance traveled):
v2=2(qEm)l
6. Solve for Final Velocity v:
Taking the square root of both sides gives:
v=√2qElm
Final Result:
The velocity acquired by the electron after traveling a distance l in the electric field is:
v=√2qElm
The electron starts from rest, so its initial velocity u=0.
The force F acting on the electron due to the electric field is given by:
F=qE
where q is the charge of the electron and E is the strength of the electric field.
According to Newton's second law, the acceleration a of the electron can be calculated using:
a=Fm=qEm
where m is the mass of the electron.
We can use the kinematic equation that relates acceleration, distance, and velocity:
v2=u2+2as
Since the initial velocity u=0, this simplifies to:
v2=2as
Substitute a=qEm and s=l (the distance traveled):
v2=2(qEm)l
Taking the square root of both sides gives:
v=√2qElm
The velocity acquired by the electron after traveling a distance l in the electric field is:
v=√2qElm
Topper's Solved these Questions
- CATHODE RAY, PHOTOELECTRIC EFFECT AND X-RAYSBOOK - BITSAT GUIDECHAPTER - CATHODE RAY, PHOTOELECTRIC EFFECT AND X-RAYSEXERCISE - BITSAT Archives
6 Videos
- ATOMIC STRUCTUREBOOK - BITSAT GUIDECHAPTER - ATOMIC STRUCTUREEXERCISE - BITSAT Archives
4 Videos
- CURRENT ELECTRICITYBOOK - BITSAT GUIDECHAPTER - CURRENT ELECTRICITYEXERCISE - Bitsat Archives
26 Videos
Similar Questions
A protons of mass m charge 2 e is released from rest in a uniform electric field of strength E .The time taken by it to travel a distance d in the field is..
View SolutionA particle of mass m and charge q is released from rest in uniform electric field of intensity E. Calculate the kinetic energy it attains afect moving a distance x between the plates.
View Solution
Knowledge Check
A protons of mass m charge c is released form rest in a uniform electric field of strength E .The time taken by it to travel a distance d in the field is
A√2demEB√2dmEeC√2dEmeD√2dEedmAn electron of mass m and charge q is accelerated from rest in a uniform electric field of strength E. The velocity acquired by it as it travels a distance l is
A√2EqlmB√2ElmlC√2EmqlD√EqmlA charge particle of mass m and charge q is released from rest in uniform electric field. Its graph between velocity (v) and distance travelled (x) will be :
A B
B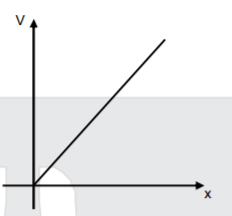 C
C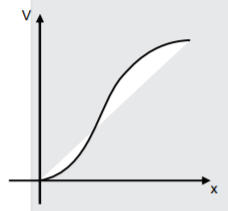 D
D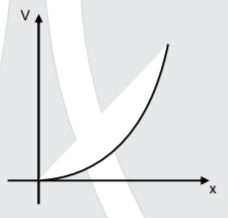
A particle of mass m and charge q is placed at rest in a uniform electric field E and then released, the kinetic energy attained by the particle after moving a distance y will be
View SolutionA particle of mass M and charge q is released from rest in a region of uniform electric field of magnitude E . After a time t, the distance travelled by the charge is S ad the kinetic energy attained by the particle is T. Then , the ratio T/S
View SolutionA particle of mass m and charge −q is released from rest in a uniform electric field. If there is no other force on the particle, the dependence of its potential energy on the distance x travelled by it is correctly given by (assume initial potential energy to be zero ,graphs are schematic and not drawn to scale)
View SolutionAn oil drop of mass m and charge +q is balanced in vaccum by a uniform electric field of intensity E. the direction of this field should be
View SolutionAn oil drop of mass m and charge +q is balanced in vaccum by a uniform electric field of intensity E. the direction of this field should be
View Solution
