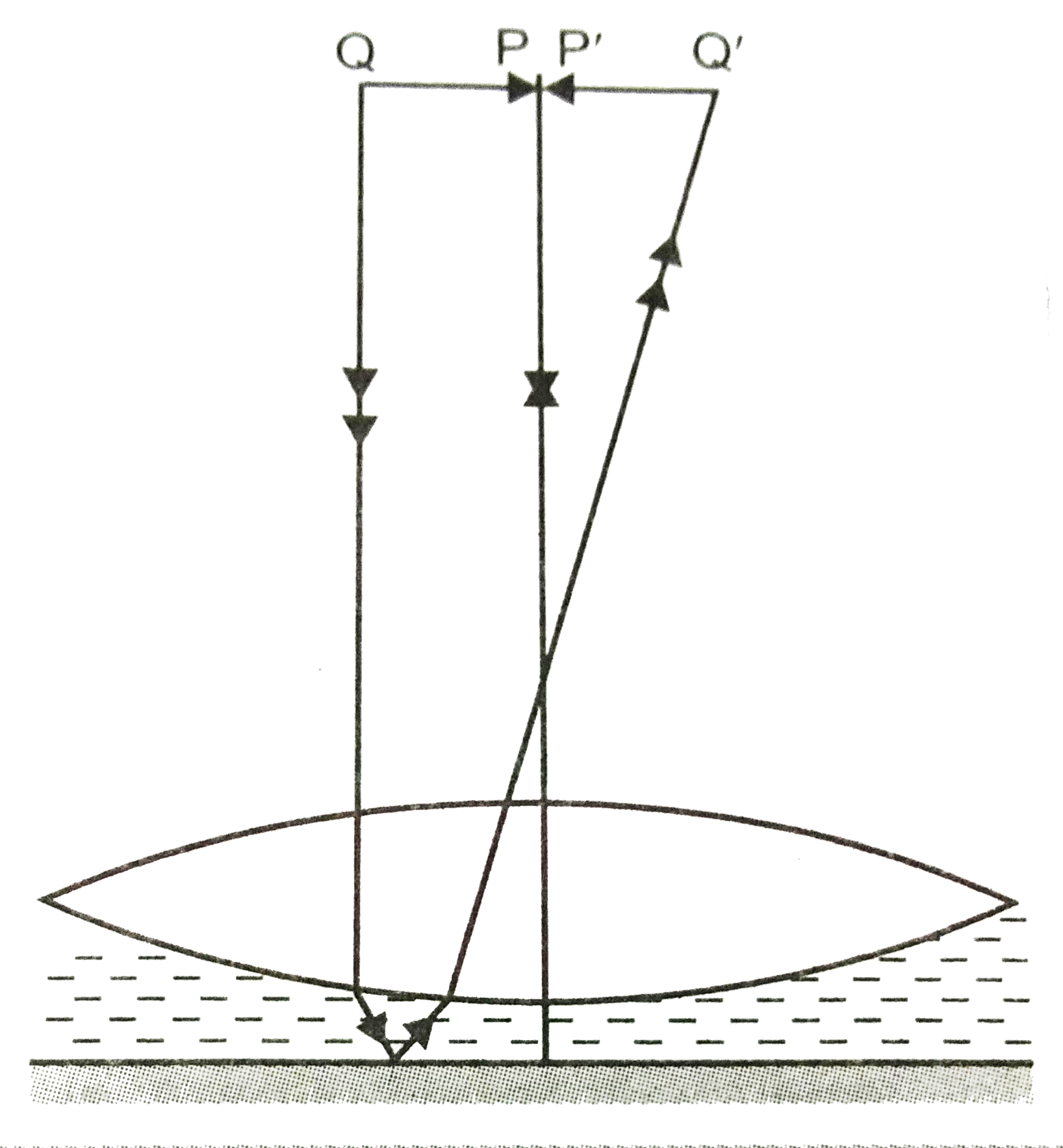
Monochromatic light rays parallel to x-axis strike a convex lens AB of refractive index . If the lens oscillates such that AB tilts upto a small angle (in radian) on either side of y-axis, then find the distance between extreme positions of oscillating image:

the image will not move
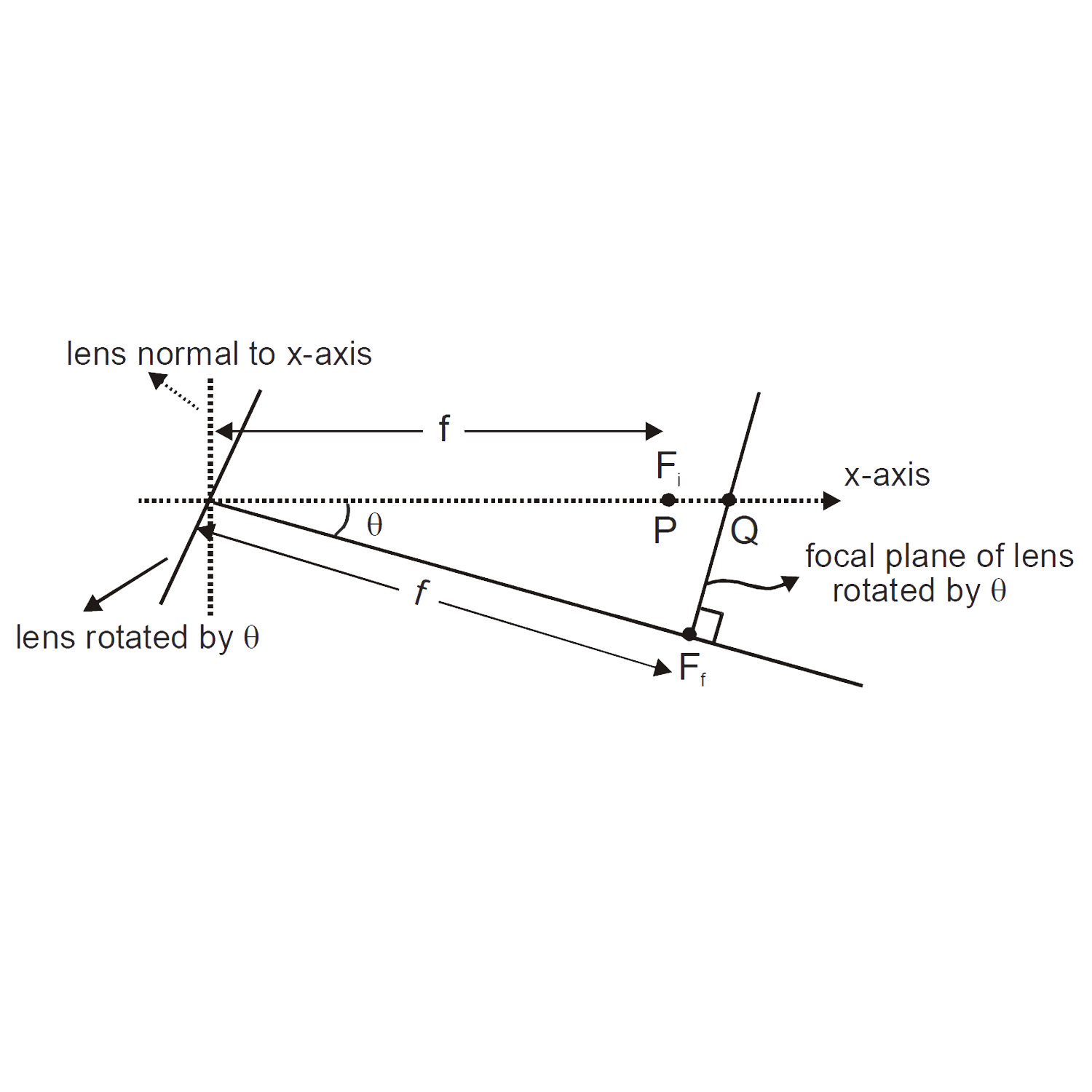
When the lens is tited by , the image is formed at the intersection (Q) of focal plane of lens in tited position and x-axis.
As the lens ocillates. The image shifts on x-axis in between P and Q
Distance between two exterme position of the image
Topper's Solved these Questions
Similar Questions
Monochromatic light rays parallel to the principal axis (the x axis) are incident on a convex lens of focal length f. If the lens oscillates such that it tilts up to a small angle θ on either side of the y axis, then find the distance between the exterme positions of the image. Take secθ≈1+θ22 for small θ.
View SolutionA parallel beam of light is incident on a lens of focal length 10 cm. A parallel slab of refractive index 1.5 and thickness 3 cm is placed on the other side of the lens. Find the distance of the final image from the lens.
 .
.
View Solution
Knowledge Check
A double convex lens made of glass (refractive index n=1.5) has the radii of curvature of both the surfaces as 20cm. Incident light rays parallel to the axis of the lens will converge at a distance L such that
AL=20cmBL=10cmCL=40cmDL=203cmA double convex thin lens made of glass (refractive index μ=1.5) has both radii of curvature of magnitude 20 cm . Incident light rays parallel to the axis of the lens will converge at a distance L such that
AL=20 cmBL=10 cmCL=40 cmDL=20/3 cm
A horizontal parallel beam of light passes though a vertical convex lens of focal length 40 cm. Behind the lens there is a plane mirror making an angle θ with the principal axis of the lens. The mirror intersects the principal axis at M. Distance between the optical centre of the lens and point M is OM=20cm. The light beam reflected by the mirror converges at a point P. Distance OP is 20 cm. Find θ.
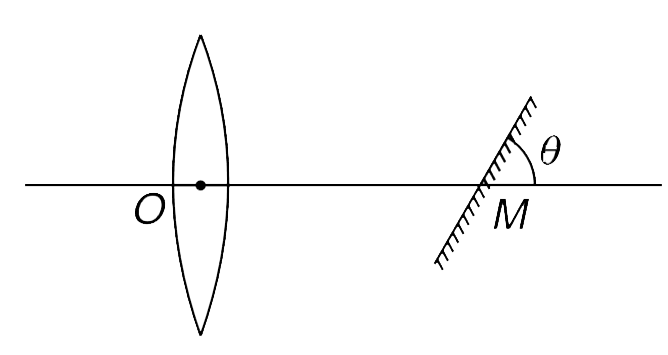
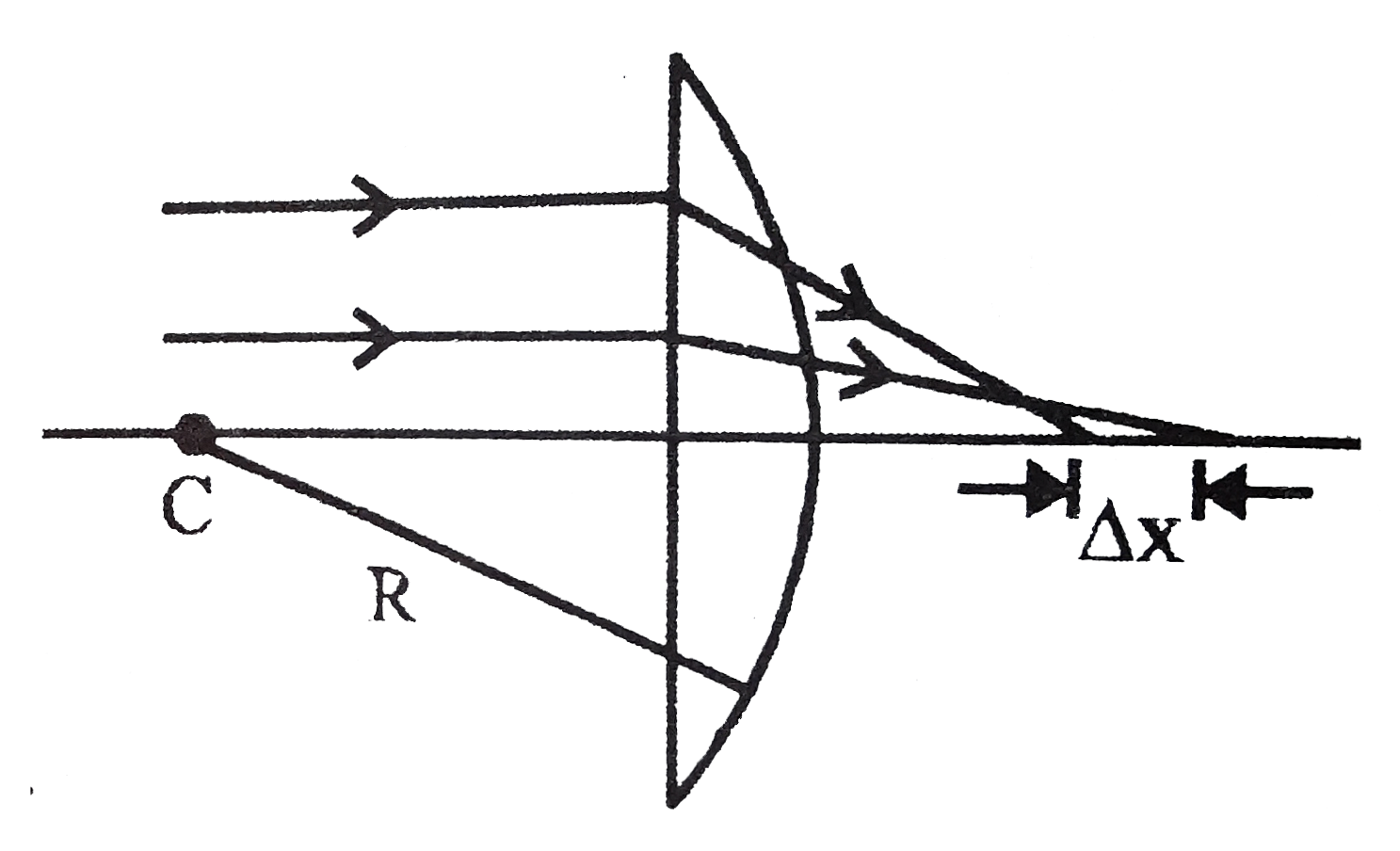
View SolutionTwo rays travelling parallel to the principal axis strike a thick large plano-convex lens having a refracive index of 1.60.If the spherical face has a radius of curvature of magnitude 20.0cm and th two rays are h1=0.500cmand h2=12.0cm from the principal axis ,find the difference in the positions where they cross the principal axis .Assume that the ray incident at height h2is incident at the periphery.
View SolutionA small point object is placed atOat a distance of0.60metre in air from a convex spherical surface of refractive index1.5.If the radius of the curvature is 25cmthen what is the position of the image on the principal axis.
View SolutionFig. shows an equiconvex lens (of refractive index 1.5) in contact with a liquid layer on top of a plane mirror. A small needle with its tip on the principal axis is moved along the axis until its inverted image is found at the position of the needle. The distance of the needle from the lens is measured to be 45.0cm. The liquid is removed and the experiment is repeated. The new distance is measured to be 30.0cm. What is the refractive index of the liquid ?
View SolutionAn object is placed at a distance of 10cmm to the left on the axis of convex lens A of focal length 20cm. A second convex lens of focal length 10cm is placed coaxially to the right of the lens A at a distance of 5cm from A. Find the position of the final image and its magnification. Trace teh path of the rays.
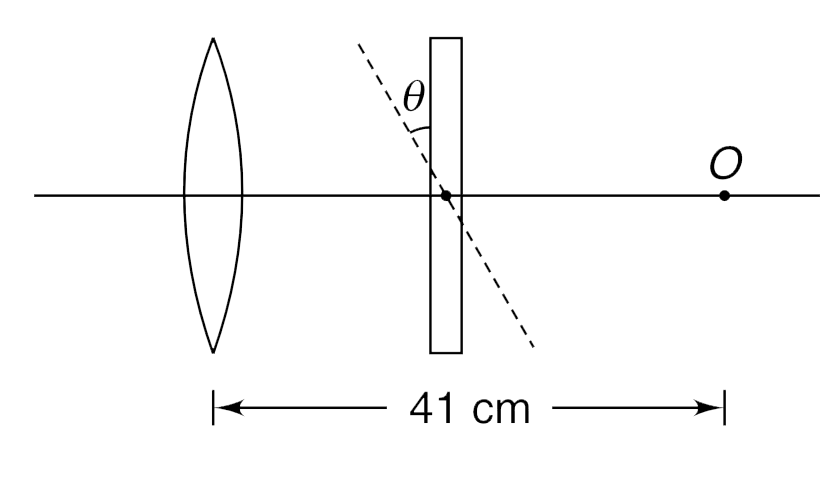
View SolutionA point object O is placed at a distance of 41 cm from a convex lens of focal length f=20 cm on its principal axis. A glass slab of thickness 3 cm and refractive index μ=1.5 is placed between the lens and the object with its faces perpendicular to the principal axis of the lens. Image of the object is formed at point I1. Now the glass slab is tilted by an angle of θ=1° (as shown in the Figure) and the final image is formed at I2. Calculate the distance between points I1 and I2. Consider only paraxial rays for the lens and near normal incidence for the glass slab.
View Solution

