Two rays travelling parallel to the principal axis strike a thick large plano-convex lens having a refracive index of 1.60.If the spherical face has a radius of curvature of magnitude 20.0cm and th two rays are h1=0.500cmand h2=12.0cm from the principal axis ,find the difference in the positions where they cross the principal axis .Assume that the ray incident at height h2is incident at the periphery.
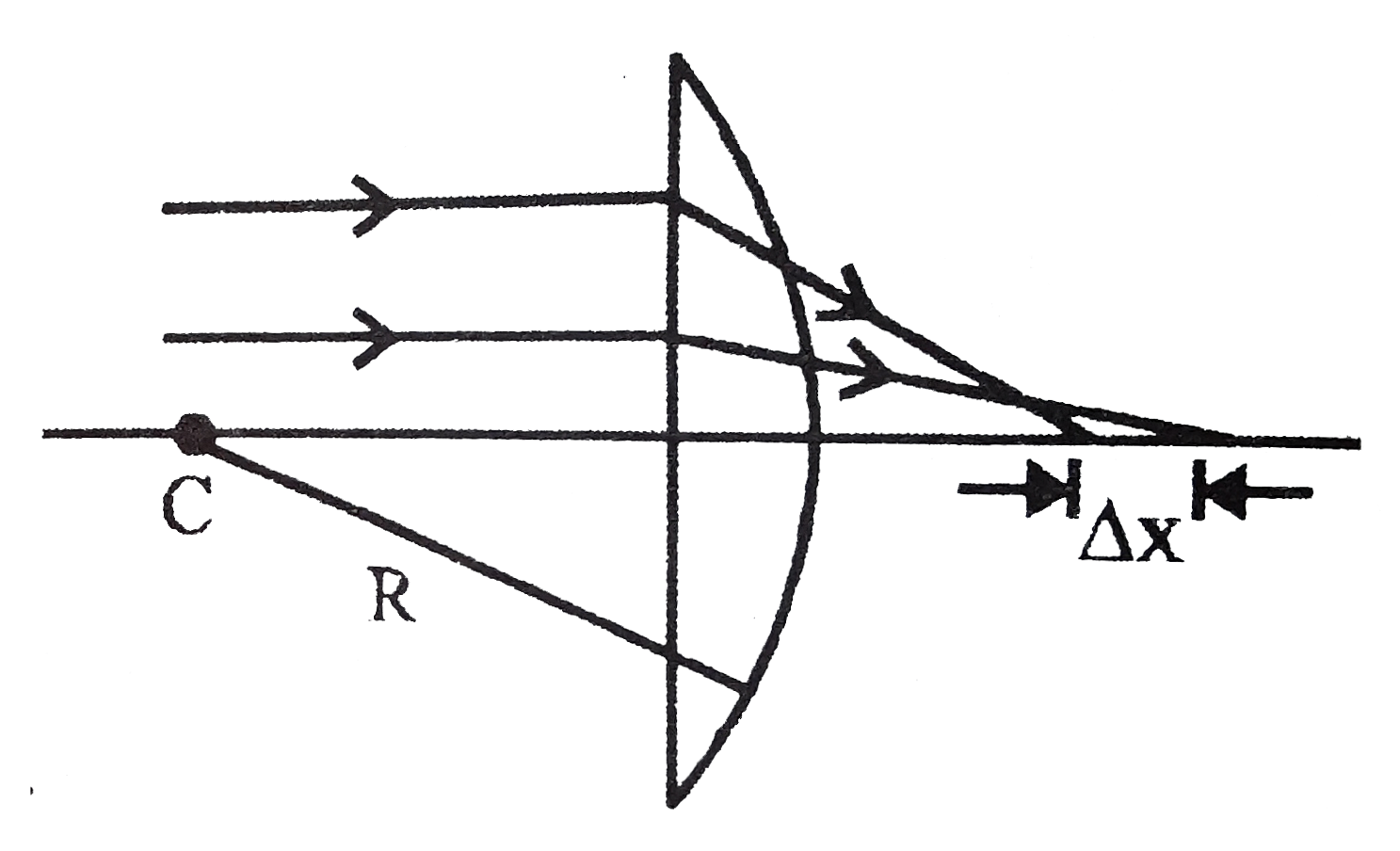
The correct Answer is:21.3cm

for ray h1
sini=1220⇒sini=35⇒sini=0.6⇒i=37∘
applying snell's law of refraction
μgsini=μasinr⇒1.6sini=sinr
sinr=0.96⇒r=74∘
δ=r−i⇒δ=74∘−37∘
δ=37∘⇒tanδ=12x1
tan37∘=12x1 ⇒x1=12tan37∘
x1=16cm
for ray h2
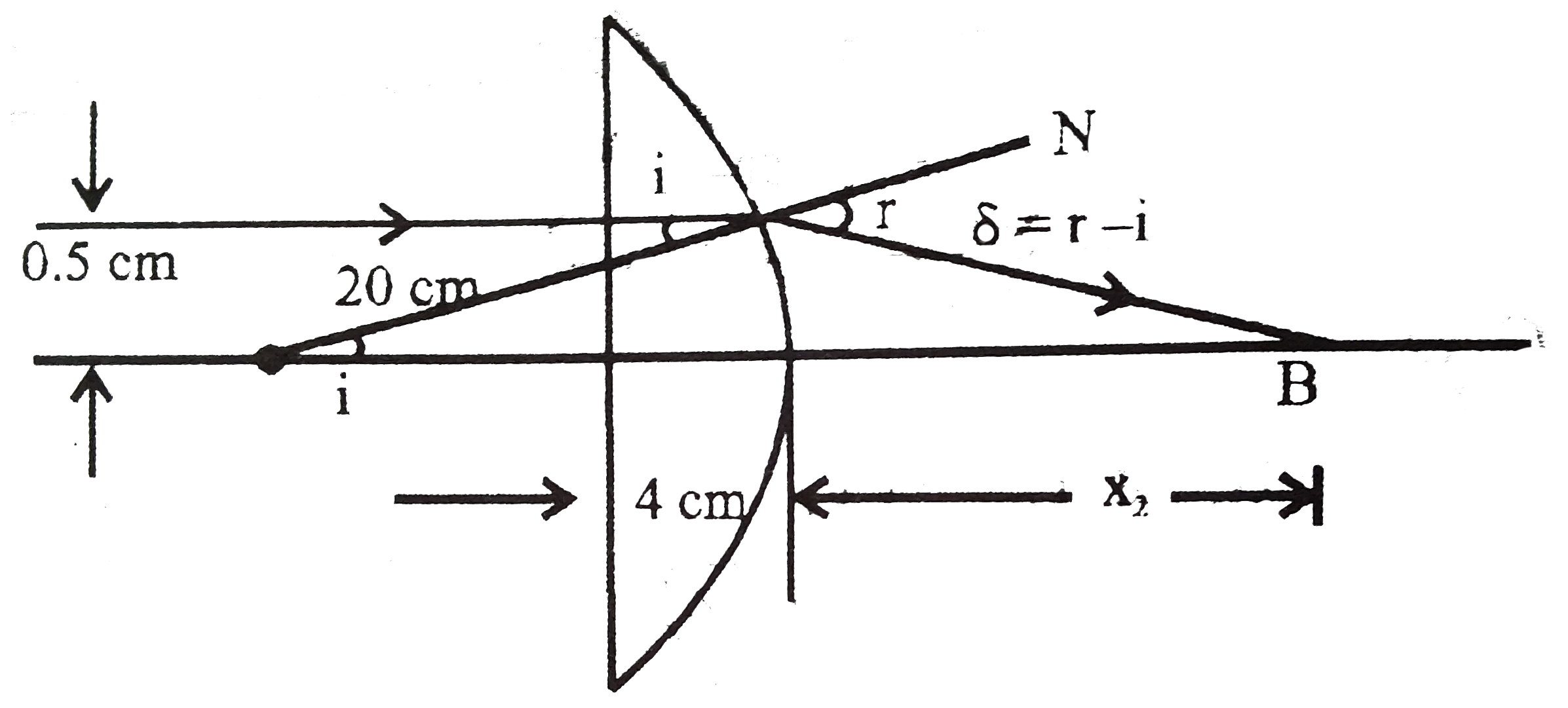
sini=0.520⇒sini=140⇒i=140 rad applying snell's law of refraction
μgsini=μasinr⇒1.6i=μar⇒=1.6×140⇒r=125
δ=r−i⇒δ=125−140⇒δ=3200
tanδ=3200⇒0.5x2=3200
x2=1003cm=33.3cm
Δx=(x2+4)−x1 ltbegt Δx=(33.3+4)−16
Δx=21.3cm
Similar Questions
Sunlight is incident on a concave mirror, parallel to its principal axis. The image is formed at a distance of 12cm from the pole. Find the radius of curvature of the mirror.
View SolutionTwo rays are incident on a spherical mirror of radius R = 5 cm parallel to its optical axis at distances h1=0.5cm and h2=3cm Determine the distance Δx between the points at which these rays intersect the optical axis after being reflected at the mirror.
View Solution
Knowledge Check
A double convex thin lens made of glass (refractive index μ=1.5) has both radii of curvature of magnitude 20 cm . Incident light rays parallel to the axis of the lens will converge at a distance L such that
AL=20 cmBL=10 cmCL=40 cmDL=20/3 cmA double convex thin lens made of glass (refractive index μ=1.5) has both radii of curvature of magnitude 20 cm . Incident light rays parallel to the axis of the lens will converge at a distance L such that
AL=20cmBL=10cmCL=40cmDL=20/3cmA light ray travelling parallel to the principal axis of a concave mirror strikes the mirror at angle of incidence θ. If radius of curvature is R, then after reflection, the ray meets the principal axis at a distance d from the centre of curvature then d is
AR2BRcosθ2CR2cosθDR2(1+cosθ)
A light ray parallel to the principal axis is incident (as shown in the figure) on a thin planoconvex lens with radius of curvature of its curved part equal to 10 cm. Assuming that the refractive index of the material of the lens is 4/3 and medium on both sides of the lens is air, find the distance of the point from the lens where this ray meets the principal axis. Find your answer in the form X7cm and fill value of X .
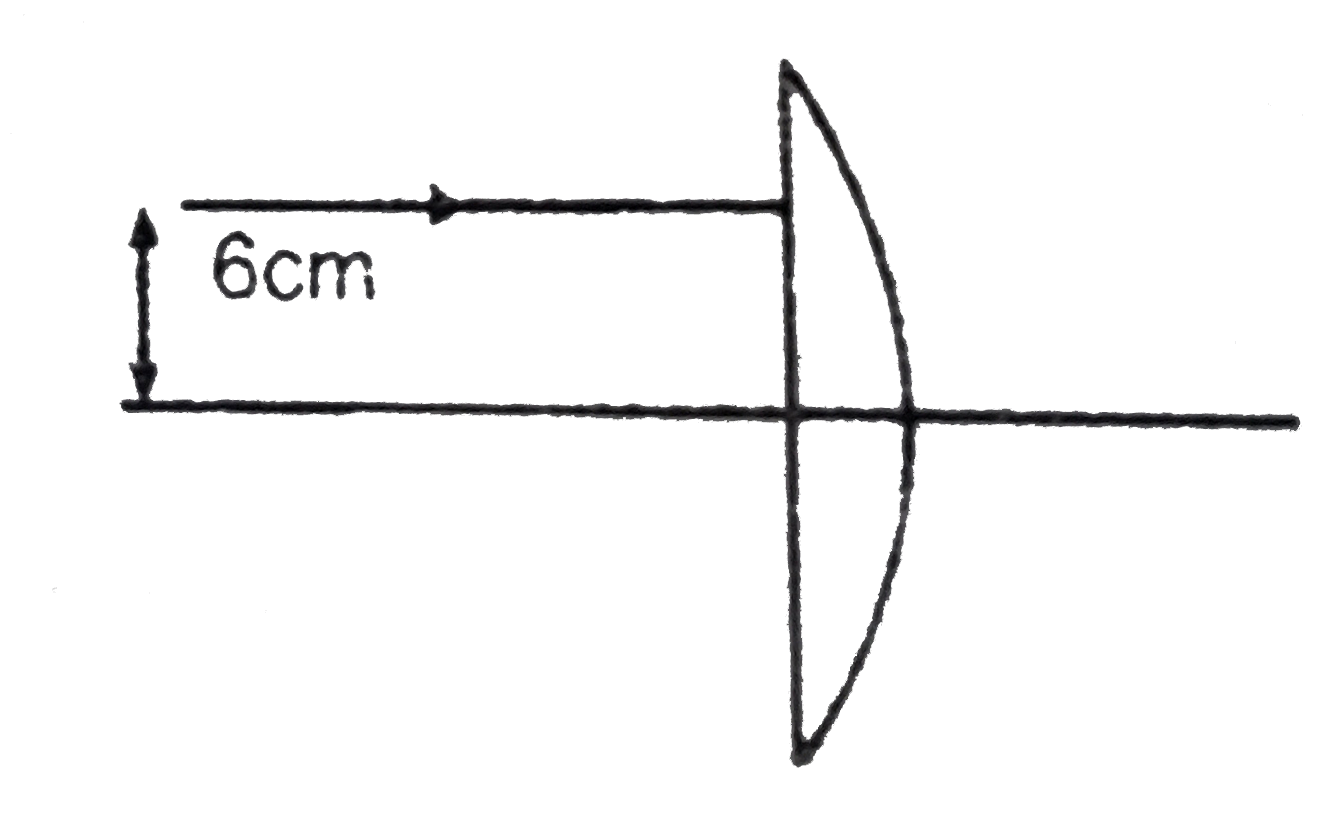
View SolutionA small point object is placed atOat a distance of0.60metre in air from a convex spherical surface of refractive index1.5.If the radius of the curvature is 25cmthen what is the position of the image on the principal axis.
View SolutionA converging beam of light rays in incident on a concave spherical mirror whose radius of curvature is 0.8m. Determine the position of the point on the optical axis of the mirror where the reflected rays intersect, if the extensions of the incident rays intersect the optical axis 40cm form the mirror's pole.
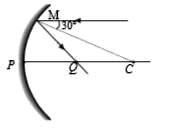
View SolutionA ray parallel to principal axis is incident at 30∘ from normal on concave mirror having radius of curvature R. The point on principal axis where rays are focussed is Q such that PQ is
View SolutionA double convex lens made of glass (refractive index n=1.5) has the radii of curvature of both the surfaces as 20cm. Incident light rays parallel to the axis of the lens will converge at a distance L such that
View Solution