A small area is removed from a uniform spherical shell of mass M and radius R. Then the gravitatioinal field intensity near the hollow portion is
GMR2
GM2R2
3GM2R2
zero
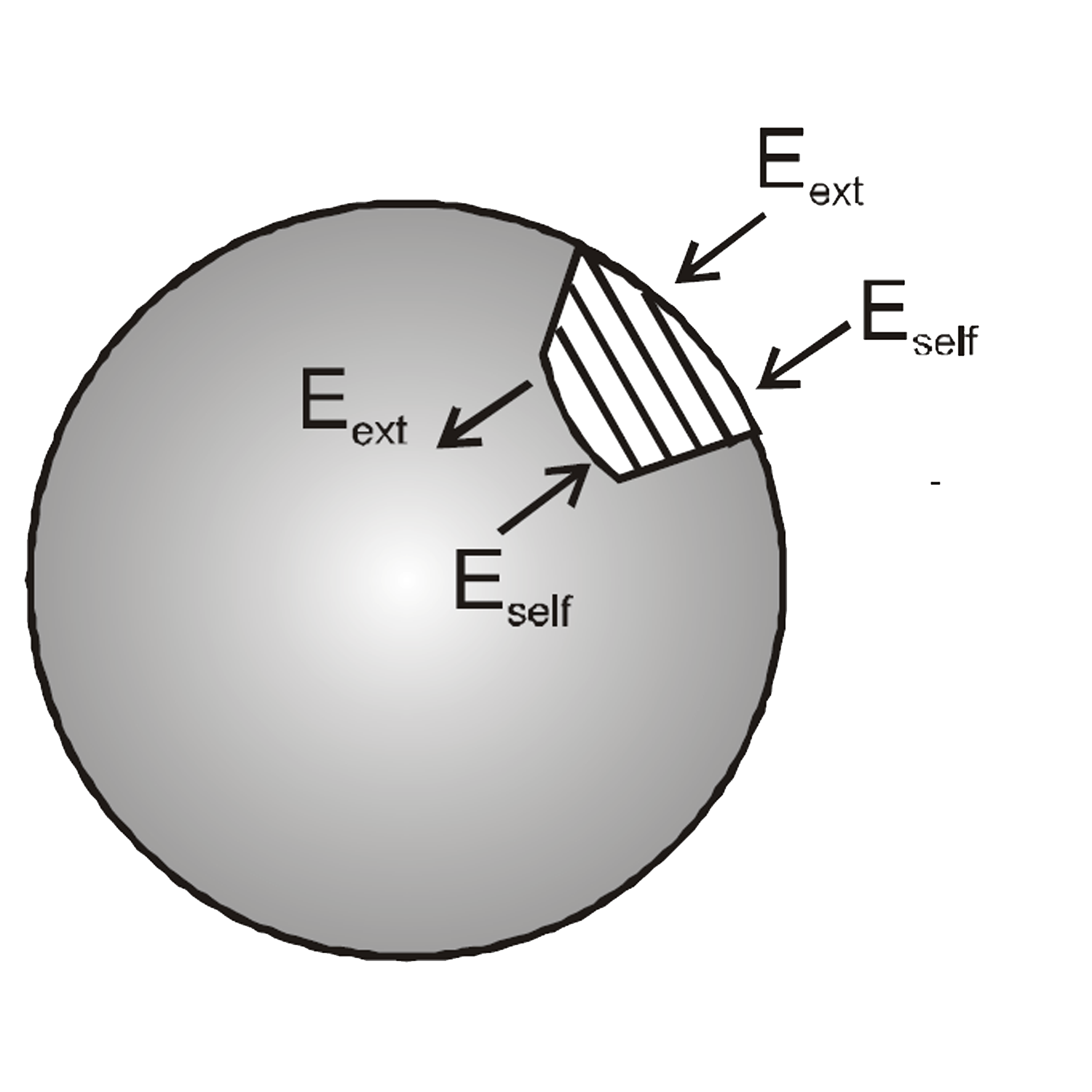
Consider a small area (shaded strip)
here Eself= gravitational field due to this strip
and Eext= gravitational field due to the rest of spherical shell.
Ein= gravitational field just inside the strip due to whole shell.
Eout= gravitaional field just outside the strip due to whole shell.
Ein=Eext−Eself=0
⇒Eext=Eself
Eout=Eext+Eself=GMR2⇒Eext=GM2R2
After the shaded area has been removed there is no Eself and no Eself and only Eext hence Enet=Eext=GM2R2
Topper's Solved these Questions
Similar Questions
For a given uniform spherical shell of mass M and radius R find gravitational field at a distancer r from centre in following two cases (a) r≥R (b) r<R .
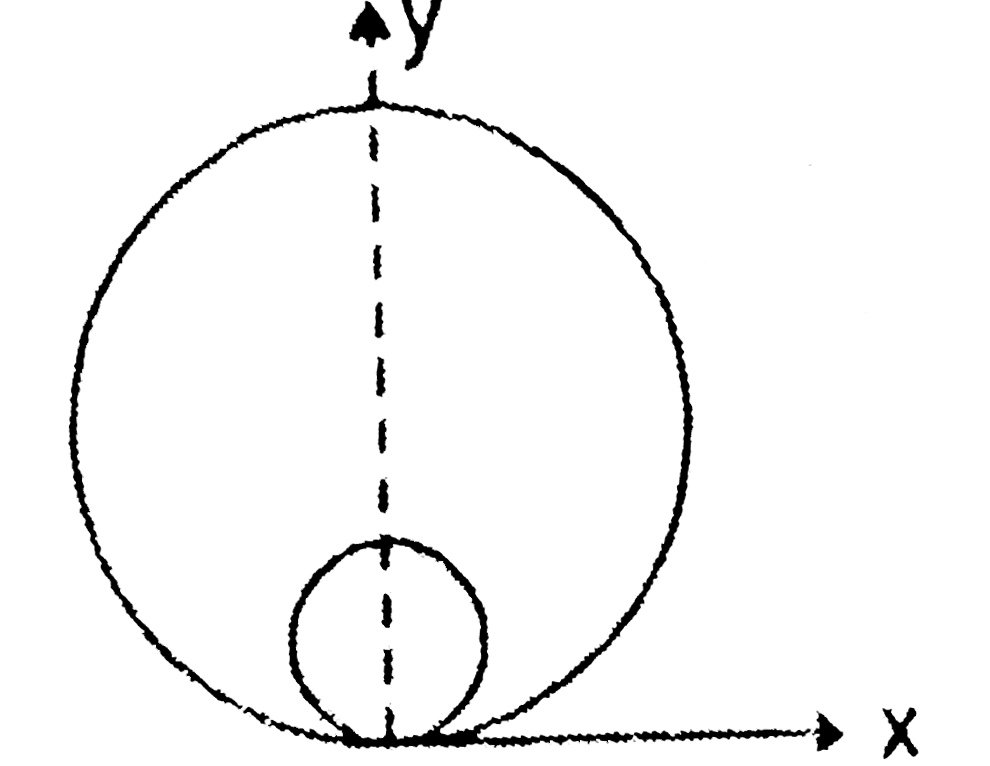
View SolutionA solid shere of mass m and radius r is placed inside a hollow spherical shell of mass 4m and radius 4r find gravitational field intensity at
(a) r<y<2r (b) 2r<y<8r (c) y>8r
here coordinate is measured from the point of contact of the sphere and the shell
 .
.
View Solution
Knowledge Check
Intensity of gravitational field inside the hollow spherical shell is
AVariableBminimumCmaximumDzeroA particel of mass M is placed at the centre of a inform spherical shell of mass 2M and radius R. The gravitational potential on the surface of the shell is
A−GMRB−3GMRC−2GMRDzeroA particle of mass m is placed at the centre of a unifrom spherical shell of mass 3 m and radius R The gravitational potential on the surface of the shell is .
A−GmRB−3GmRC−4GmRD−2GmR
A particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA mass of 50 kg is placed at the centre of a uniform spherical shell of mass 100 kg and radius 50 m. If the gravitational potential at a point, 25 m from the centre is V kg/m. The value of V is:
View SolutionA particle of mass m is located inside a spherical shell of mass M and radius R. The gravitational force of attraction between them is
View SolutionA point mass m0 is placed at distance R/3 from the centre of spherical shell of mass m and radius R. the gravitational force on the point mass m0 is
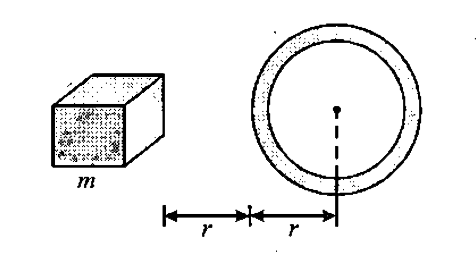
View SolutionA block of mass m is lying at a distance r from a spherical shell of mass m and radius r, then :
View Solution

