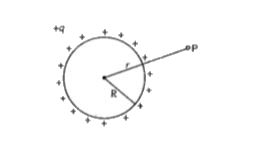
Statement 1:Electric field intensity at surface of uniformly charged spehrical shell is $E$ if the shell is puncurted at a point then intensity at punctured point becomed $E / 2$ .
Statement 2:Electric field intensity due to spherical charge distribution can be found out by using $G a u s s L a w$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$V_{P} = \frac{1}{4 π ε_{0}} [\frac{q}{r_{1}} + \frac{- K q}{r_{2}}] = 0 or r_{2} = K r_{1}$
$V_{P} = \frac{1}{4 π ε_{0}} [\frac{q}{r_{1}} + \frac{- K q}{r_{2}}] = 0 or r_{2} = K r_{1}$ (B) Now , $P P_{1} = \frac{sin (∠ P O P_{1})}{sin (∠ P A P_{1})} = \frac{r_{2}}{r_{1}} = \frac{K r_{1}}{r_{1}} = K$
$(C) O P_{1} = x, P_{1} A = (6 - x)$
$r_{1}^{2} = x^{2} + y^{2} r_{2}^{2} = {(6 - x)}^{2} + y^{2} = 4 (x^{2} + y^{2})$
$r_{2} = 2 r_{1}$ (from $r_{2} = K r_{1}) (6 - x^{2}) + y^{2} = 4 (x^{2} + y^{2})$ ltbr> On solving ${(x + 2)}^{2} + {(y = 0)}^{2} = {(4)}^{2}$
Locus of point $P$ is a circle of radius $x_{1} = 4 m$ and centre $x (2) = (- 2, 0)$
(d) the values of $O A$ and $K$ should be known.

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Electric field intensity at a point a hollow charged spherical conductor
Ais zero
Bis constant
Cincrease with the distance from the centre of the sphere
Dnone of these
Question 2 - Select One
The electric field intensity on the surface of a charged conductor is
Azero
Bdirected normally to the surface
Cdirected tangentially to the surface
Ddirected along $45^{\circ}$ to the surface
Question 3 - Select One
The electric field intensity on the surface of a charged conductor is
Azero
Bdirected normally to the surface
Cdirected tangentially to the surface
Ddirected along $45^{\circ}$ to the surface

NARAYNA-ELECTROSTATICS AND GAUSS LAW-ASSERTION AND REASON

Home
Ask Doubt
Profile