Which one of the following plots represents the variation of the gravitational field on a particle with distance r due to a thin spherical shell of raduis R? (r is measured from the centre of the spherical shell).


The correct Answer is:B
To determine the variation of the gravitational field g on a particle with distance r due to a thin spherical shell of radius R, we can analyze the gravitational field in two distinct regions: inside the shell and outside the shell.
1. Understanding the Region Inside the Shell:
- When the particle is located inside the thin spherical shell (i.e., r<R), the gravitational field g is zero. This is a result of the shell theorem, which states that a uniform spherical shell of mass exerts no net gravitational force on a particle located inside it.
- Therefore, for r<R:
g=0
2. Understanding the Region Outside the Shell:
- When the particle is outside the shell (i.e., r≥R), the gravitational field can be calculated using the formula:
g=GMr2
where G is the gravitational constant and M is the mass of the shell. Since the mass M remains constant, we can see that g is inversely proportional to the square of the distance r.
- Thus, for r≥R:
g∝1r2
3. Plotting the Graph:
- Now, we can plot the gravitational field g against the distance r:
- For r<R, g=0.
- At r=R, the gravitational field starts to increase as g becomes proportional to 1r2.
- As r increases beyond R, g decreases following the 1r2 relationship.
4. Identifying the Correct Plot:
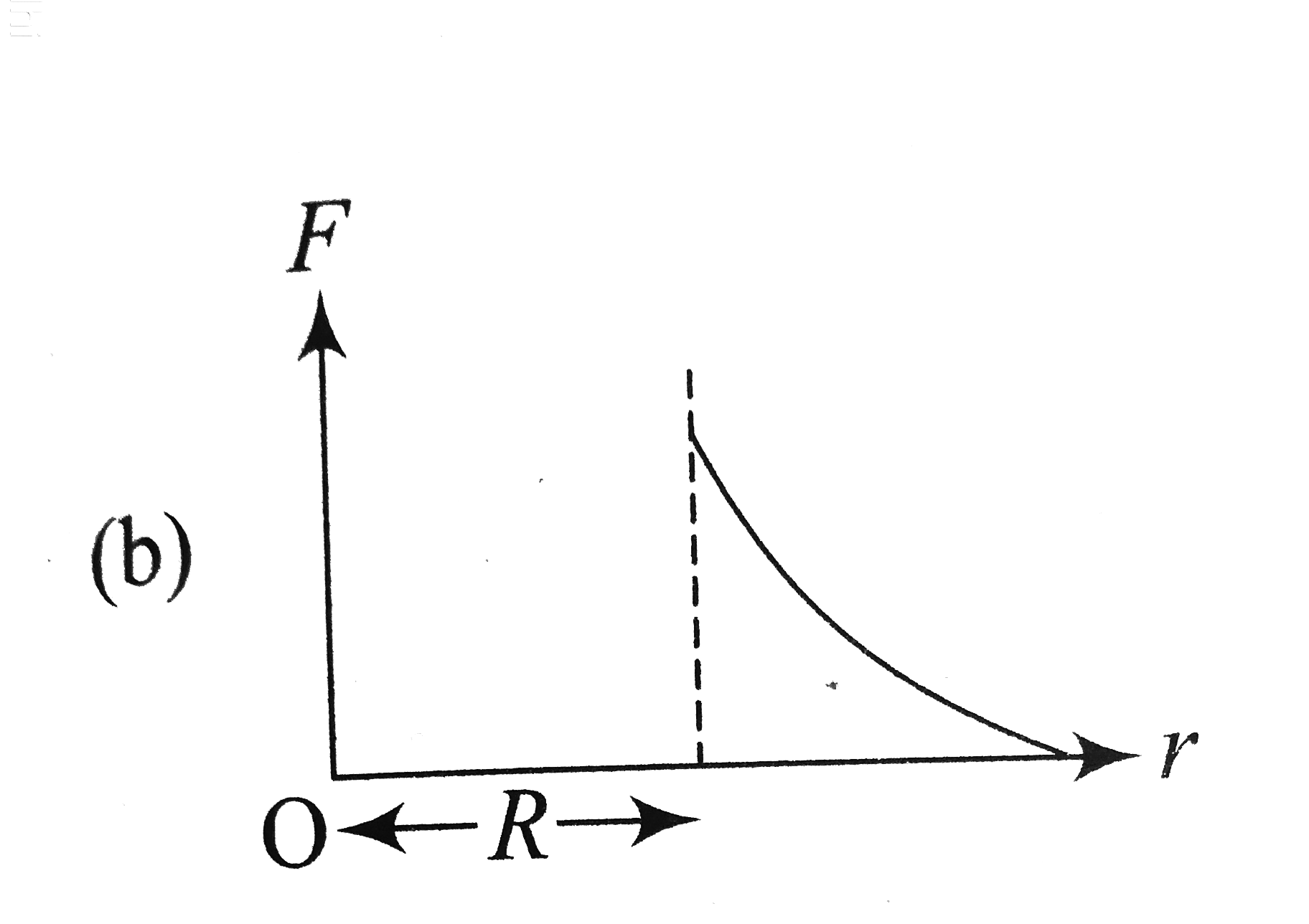
- The graph will start at zero for r<R and will then show a decreasing curve for r≥R. This behavior matches with option B in the provided choices.
Final Answer:
The correct plot representing the variation of the gravitational field g on a particle with distance r due to a thin spherical shell of radius R is option B.
---
- When the particle is located inside the thin spherical shell (i.e., r<R), the gravitational field g is zero. This is a result of the shell theorem, which states that a uniform spherical shell of mass exerts no net gravitational force on a particle located inside it.
- Therefore, for r<R:
g=0
- When the particle is outside the shell (i.e., r≥R), the gravitational field can be calculated using the formula:
g=GMr2
where G is the gravitational constant and M is the mass of the shell. Since the mass M remains constant, we can see that g is inversely proportional to the square of the distance r.
- Thus, for r≥R:
g∝1r2
- Now, we can plot the gravitational field g against the distance r:
- For r<R, g=0.
- At r=R, the gravitational field starts to increase as g becomes proportional to 1r2.
- As r increases beyond R, g decreases following the 1r2 relationship.
- The graph will start at zero for r<R and will then show a decreasing curve for r≥R. This behavior matches with option B in the provided choices.
The correct plot representing the variation of the gravitational field g on a particle with distance r due to a thin spherical shell of radius R is option B.
Topper's Solved these Questions
- GRAVITATIONBook:A2ZChapter:GRAVITATIONExercise:AIIMS Questions
Explore 21 Videos
- GRAVITATIONBook:A2ZChapter:GRAVITATIONExercise:Chapter Test
Explore 29 Videos
- GRAVITATIONBook:A2ZChapter:GRAVITATIONExercise:Assertion Reasoning
Explore 16 Videos
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBook:A2ZChapter:GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONExercise:Chapter Test
Explore 30 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBook:A2ZChapter:KINETIC THEORY OF GASES AND THERMODYNAMICSExercise:Chapter Test
Explore 29 Videos
Similar Questions
Which one of the following graphs represents the variation of electric field with distance r from the centre of a charged spherical conductor of radius R?
View SolutionFind the gravitational potential due to a spherical shell of mass M and radius R at r<R and r>R, where r is the distance from the centre of the shell.
View Solution
Knowledge Check
Which one of t he following plots represents the variation of gravitational field of a particle with distance r due to thin spherical shell of radius R ?
A B
B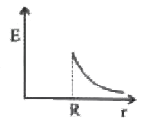 C
C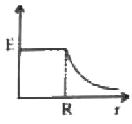 D
D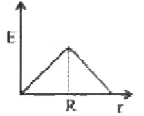
Which one of the following graphs represents correctly represent the variation of the gravitational field (E) with the distance (r) from the centre of a spherical shell of mass M radius R ?
A B
B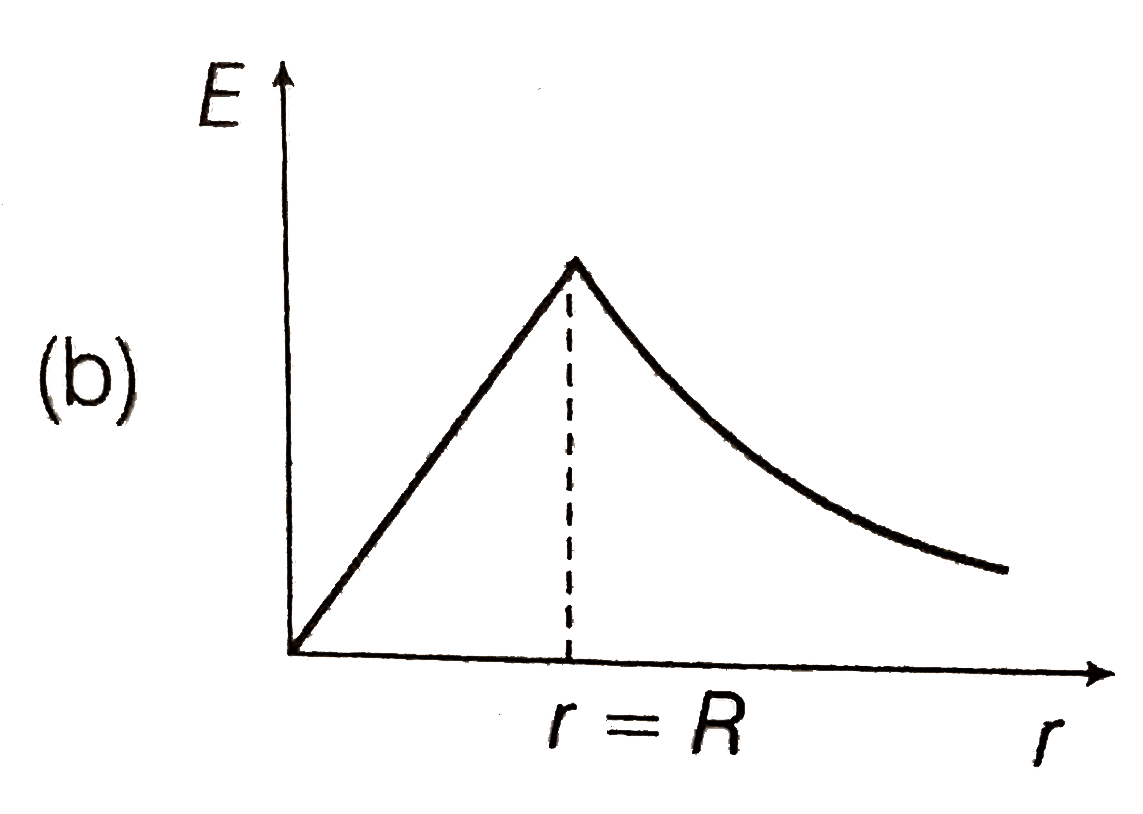 C
C D
D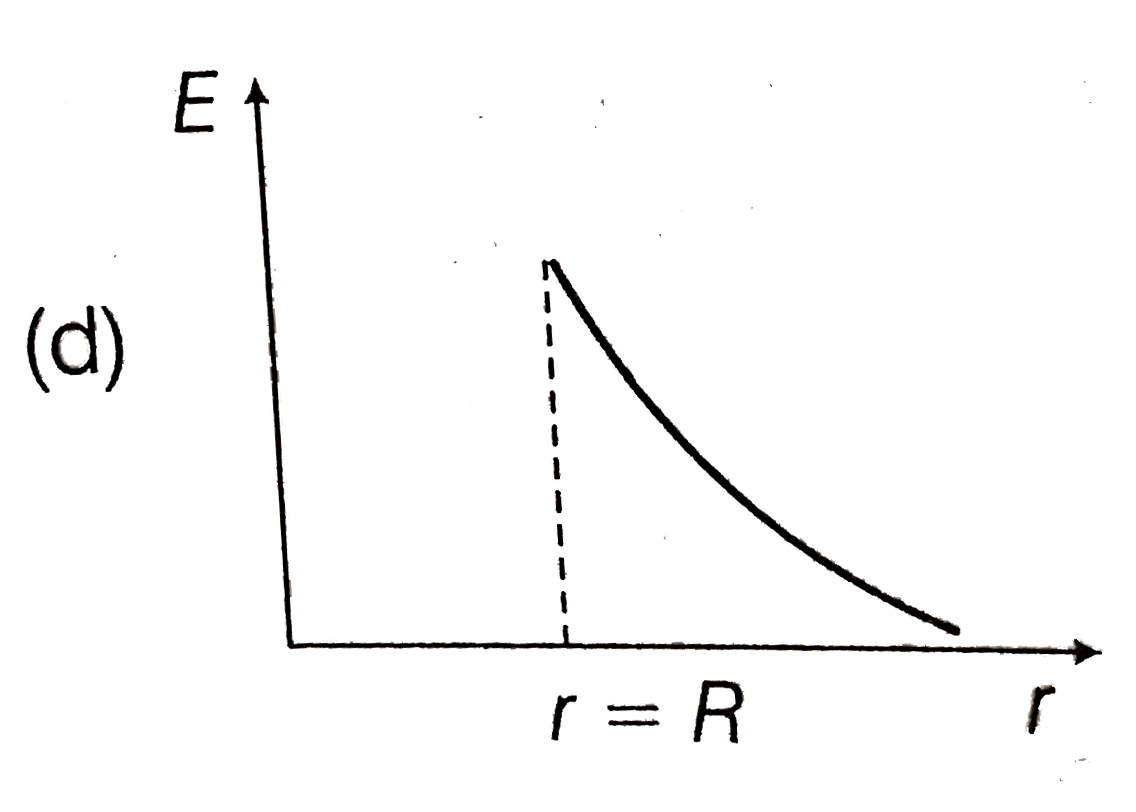
Which of the following graph represents the variation of electric field E due to a thin charged spherical shell of radius R as a function of the distance r from the centre of the shell?
A B
B CD
CD
What is the intensity of gravitational field of the centre of a spherical shell
View SolutionThe electric field at a distance 3R2 from the centre of a charged conducting spherical shell of radius R is E. The electric field at a distance R2 from the centre of the sphere is :
View SolutionThe electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View SolutionThe electric field at a distance 3R2 from the centre of a charged conducting spherical shell of radiu R is E. The electric field at a distance R2 from the centre of the sphere is:
View SolutionThe electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
View Solution

