A partical originally at rest at the highest point of a smooth vertical circle is slightly displaced. It will leave the circle at a vertical distance h below the highest points, such that h is equal to
R
R/4
R/2
R/3
The correct Answer is:D
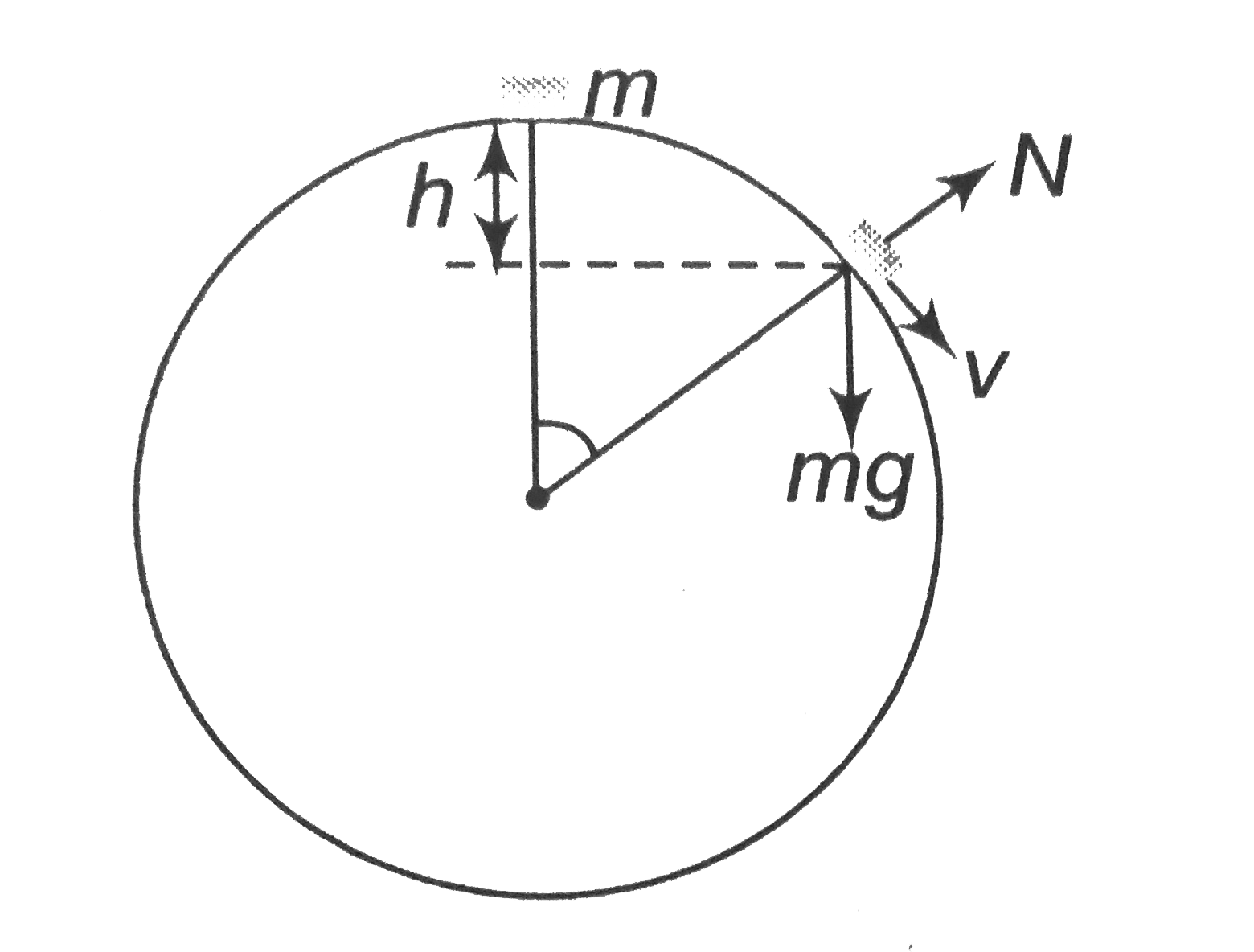
h=R−Rcosθ:v=√2gh=√2gR(1−cosθ)
mgcosθ−N=mv2/R
when it leavels circule : N=0
mgcosθ=mv2g⇒cosθ=23
h = R-R cos theta = R//3
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Collision
Explore 31 Videos
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Problems Based On Mixed Concepts
Explore 32 Videos
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Mechanical Power
Explore 25 Videos
- WAVES AND ACOUSTICSBook:A2ZChapter:WAVES AND ACOUSTICSExercise:Chapter Test
Explore 30 Videos
Similar Questions
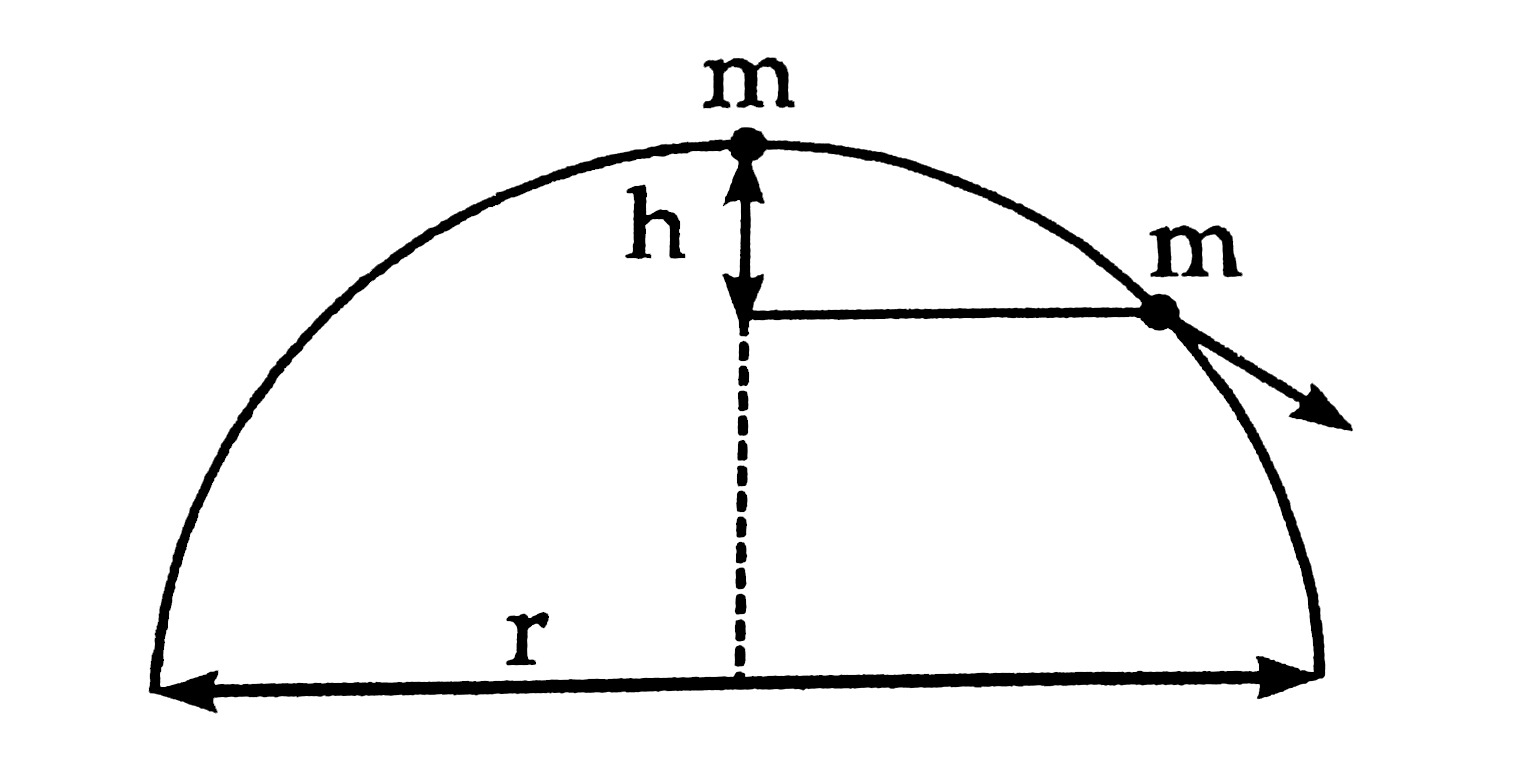
A small body of mass m slide without friction from the top of a hemispherical cup of radius r as shown in figure. If leaves the surface to the cup at vertial distance h below the highest point then
View SolutionA particle is projected along the inner surface of a smooth vertical circle of radius R, its velocity at the lowest point being (1/5)(√95gR). If the particle leaves the circle at an angular distance cos−1(x/5) from the highest point, the value of x is.
View Solution
Knowledge Check
A player throws a ball vertically upwards with velocity u. At highest point,
Aboth the velocity and acceleration of the ball are zero.Bthe velocity of the ball is u but its accelerationCthe velocity of the ball is zero but its acceleration is g.Dthe velocity of the ball is u but its acceleration is g.In a vertical circle the minimum or critical velocity at highest point of path will be
A√2rgB√rgCrωDzeroIn figure, a particle is placed at the highest point A of a smooth sphere of radius r. It is given slight push, and it leaves the sphere at B, at a depth h vertically below A. The value of h is
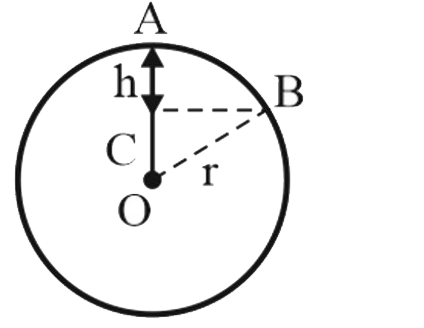 Ar6B14rC13rD12r
Ar6B14rC13rD12r
Particle slides down the surface of a smooth fixed sphere of radius r starting from rest at the highest point. Find where it will leave the sphere. Show that it strike the horizontal plane through the lowest point of the sphere at a distance equal to 5[√5+4√2](r/27) from the vertical diameter.
View SolutionA particle tied to a string describes a vertical circular motion of radius r continually. If it has a velocity √3gr at the highest point, then the ratio of the respective tensions in the string holding it at the highest and lowest points is
View SolutionA particle slides from rest from the topmost point of a vertical circle of radius r along a smooth chord making an angle θ with the vertical. The time of descent is .
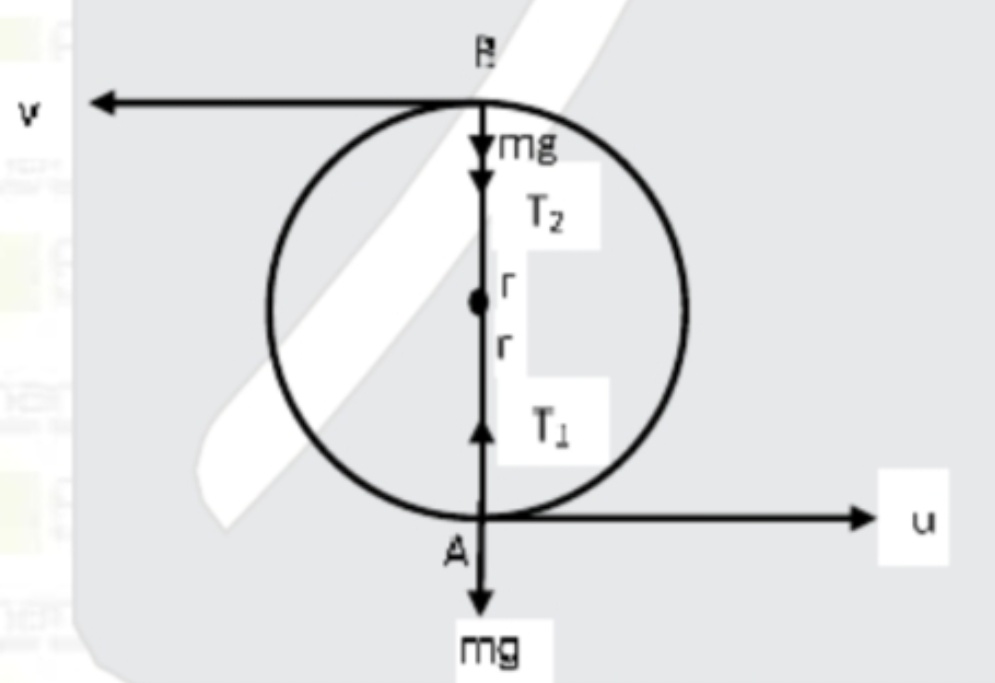
View SolutionA particle is projected so as to just move along a vertical circle of radius r. The ratio of the tension in the string when the particle is at the lowest and highest point on the circle is -
View SolutionA particle is moving in a vertical circle with radius 1 m. It the ratio of TmaxTmin=5 find the velocity at highest point ?
View Solution

