A partical is moving in the vertical plane . It is attached at one end of a string of length l whose other end is fixed. The velocity at the lower point is u. The tension in the string is →T and velocity of the partical is →v at any position. Then, which of the following quantity will remain constant.
→T.→v
kinetic energy
Gravitational potential energy
→T×→v
The correct Answer is:A
The tension vector →T is always normal to velocity vector. Hence →T.→v is always zero.
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Collision
31 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Problems Based On Mixed Concepts
32 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Mechanical Power
25 Videos
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test
30 Videos
Similar Questions
A body tied at the end of a string of length ' l' is rotated on a vertical circle. The velocity of the body at the highest point is √2gl .The maximum velocity of the body would be
View SolutionA body tied to one end of a string is made to revolve in a vertical circle. Derive an expression for the velocity of the body and tension in the string at any point.
View Solution
Knowledge Check
A particle is moving in a circular path in the vertical plane. It is attached at one end of a string of length l whose other end is fixed. The velocity at lowest point is u. The tension in the string T and acceleration of the particle is a any position. Then T is zero at highest point if
Au>√5glBu=√5glCBoth (a) and (b) are correctDBoth (a) and (b) are wrongA heavy particle is attached to one end of a string 1m long whose other end is fixed at O. It is projected from it lowest position horizontally with a velocity V:
AIf V2>5 g the particle will describe complete circular motion in the vertical planeBIf V2=3.5 g the tension in the string will become zero after the string has turned through 120∘CIf V2=2 g, the tension in the string becomes zero the velocity of the particle also becomes zeroDIf V2=g the velocity of the particle becomes zero after the string turns through 60∘A particle of maas m is attched to a light string of length l, the other end of which is fixed. Initially the string is kept horizontal and the particle is given an upwrd velocity v. The particle is just able to complete a circle
AThe string becomes slack when the partice reaches its highest pointBThe velocity of the particle becomes zero at the highest point.CThe kinetic energy of the ball in initial position was 12mv2=mgDThe particle again passes through the initial position.
A stone is attached to one end of a string and rotated in a vertical circle . If the string breaks at the position of maximum tension , then it will break at
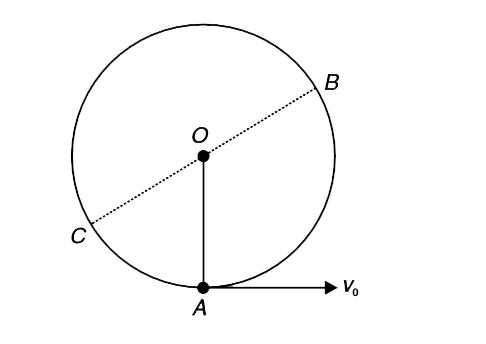
View SolutionA heavy particle is attached to one end of a light string of length l whose other end is fixed at O. The oarticle is projectyed horizontally with a velocity v0 from its lowest position A. When the angular displacement of the string is more than90∘, the particle leaves the circular path at B. The string again becomes taut at C such that B,O,C are collinear. Find v0 in terms of l and g
View Solution
A ball is attached to a string of length L and the ball is given velocity v0 at its lowest point. Find the speed of the ball at point B,C and D. Assume that the ball is moving in vertical circle.
View SolutionA body of mass m is tied to a string of length l and whirled in a verticle cirlce. The velocity of the body at the lowest position is u. Then the tension in the string at a position when the string makes an angle θ with the vertical is
View SolutionA particle is rotated in a vertical circle by connecting it to a string of length l and keeping the other end of the string fixed. The minimum speed of the particle when the string is horizontal for which the particle will complete the circle is
View Solution
