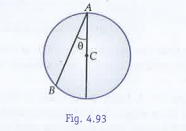
A particle slides from rest from the topmost point of a vertical circle of radius r along a smooth chord making an angle θ with the vertical. The time of descent is .
Least for θ=0
Maximum for θ=0
Least for θ=45
Independent of θ
The correct Answer is:D
a=gsina=gsin(90∘−θ)
l=2Rcosθ
Now using sut+12at2, we get
l=0t+12gcosθt2
⇒2Rcosθ=12gcosθt2⇒t=2√Rg
 .
.
this is independent of θ .
Topper's Solved these Questions
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Graphical Concept
Explore 17 Videos
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Graphical cancept
Explore 1 Video
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Subjective
Explore 29 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise Integer
Explore 9 Videos
Similar Questions
A glass marble slides from rest from the topmost point of a vertical circle of radius r along a smooth chord. Does the time of descent depend upon the chord chosen ?
View SolutionA ball of mass m is suspended from a rope of length L. It describes a horizontal circle of radius r with speed v. the rope makes an angle θ with vertical given by sinθ=r/2. Determine (a) the tension in the rope and (b) the speed of the ball. (c) time period of ball.
View Solution
Knowledge Check
A particle slides from rest from the topmost point of a vertical circle of radius r along a smooth chord making an angle θ with the vertical. The time of descent is .
ALeast for θ=0BMaximum for θ=0CLeast for θ=45DIndependent of θA conical pendulum of length L makes an angle θ with the vertical. The time period will be
 A2π√lcosθgB2π√LgcosθC2π√LtanθγD2π√Lgtanθ
A2π√lcosθgB2π√LgcosθC2π√LtanθγD2π√LgtanθInside a smooth hemispherical cavity, a particle P can slide freely. The block having this cavity is moving with constant acceleration a = g (where g is acceleration due to gravity). The particle is released from the state of rest from the topmost position of the surface of the cavity as shown. The angle θ with the vertical, when the particle will have maximum velocity with respect to the block is
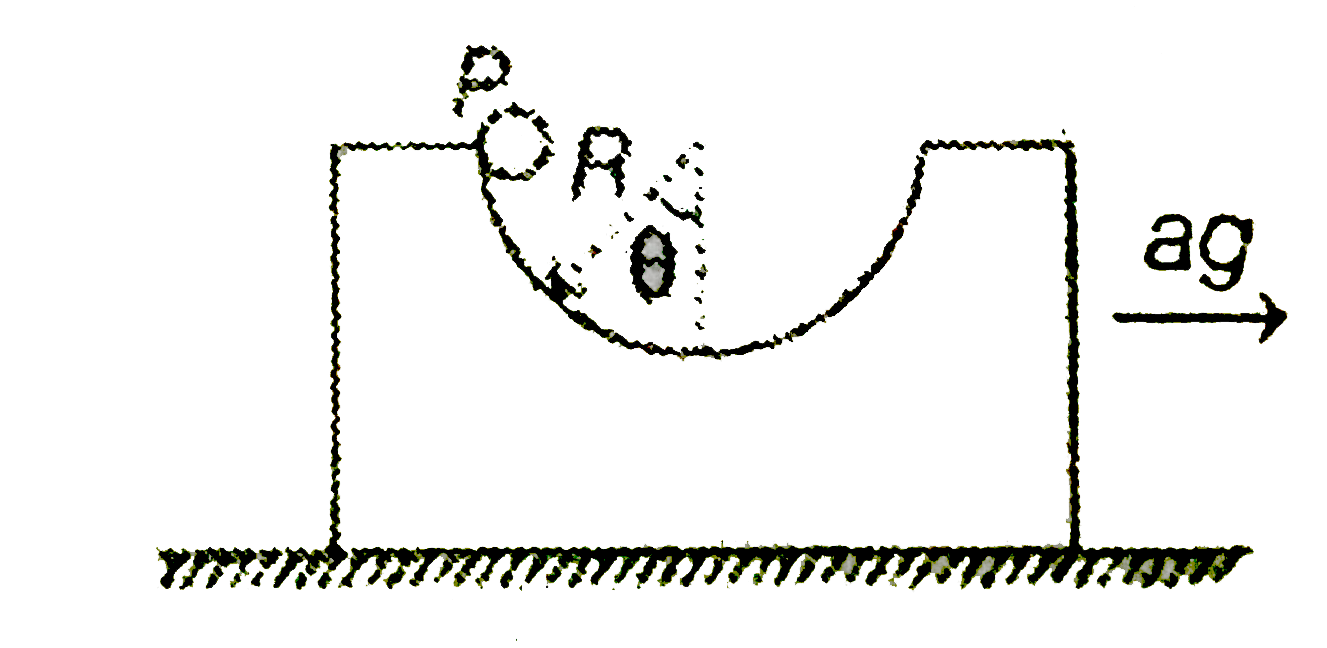 A45∘B60∘C30∘D0∘
A45∘B60∘C30∘D0∘
A force of 10.5 N acts on a particle along a direction making an angle of 370 with the vertical. Find the component of the force in the vertical direction.
View SolutionA particle is projected so as to just move along a vertical circle of radius r. The ratio of the tension in the string when the particle is at the lowest and highest point on the circle is -
View SolutionA particle crosses the topmost point C of a vertical circle with critical speed , then the ratio of velocities at points A, B and C is

View SolutionA stone tied to a string of length l is whirled in a horizontal circle at a constant angular speed ω in a circle of radius r. If the string makes an angle θ with vertical then the tension in the string is :
View SolutionPQ is a smooth inclined plane whose angle θ can be varied in such a way that point Q remains fixed and P can move on a vertical line PR. A particle slides from rest from point P at different value of θ time for descent from P and Q is noted. The following statement (s) is / are correct about the time of descent :

View Solution

