A small body of mass m slide without friction from the top of a hemispherical cup of radius r as shown in figure. If leaves the surface to the cup at vertial distance h below the highest point then
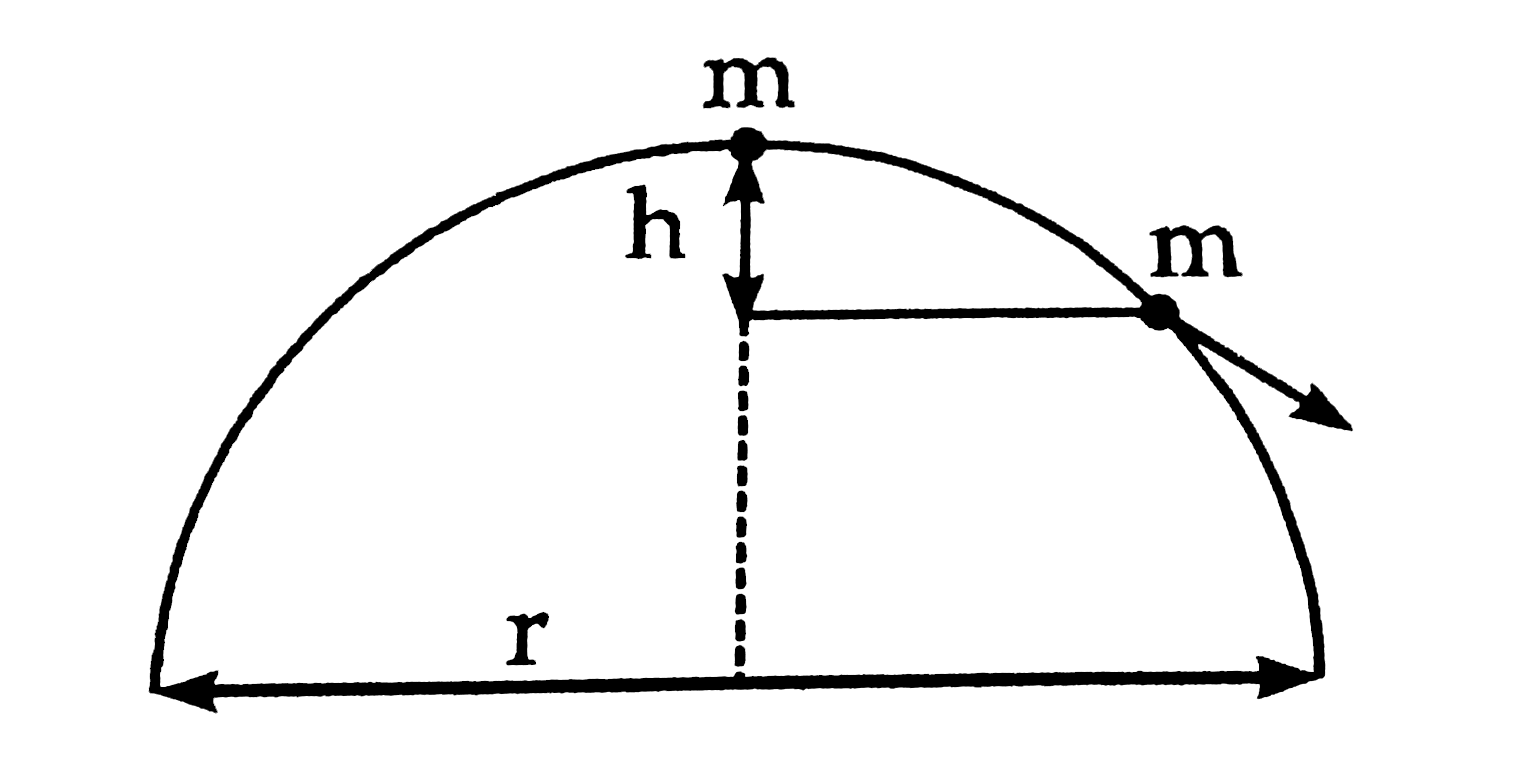
h=r
h=r/2
h=r/3
2r/3
The correct Answer is:C
From figure,

gcosθ=v2r
v2=grcosθ
cosθ=r−hr
∴v2=gr(r−h)r=g(r−h)...…(i)
By third kinematical equation of motion
v2=2gh ........(ii)
From equation (i) and (ii)
g(r−h)=2gh
∴h=r3
Topper's Solved these Questions
Similar Questions
Knowledge Check
A small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure Choose the wrong option.
 AAcceleration of block is constant throughoutBAcceleration of block is g at ACAcceleration of block is 3g at BDAcceleration of block is 2g at B
AAcceleration of block is constant throughoutBAcceleration of block is g at ACAcceleration of block is 3g at BDAcceleration of block is 2g at BA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure. Choose the wrong option (s)
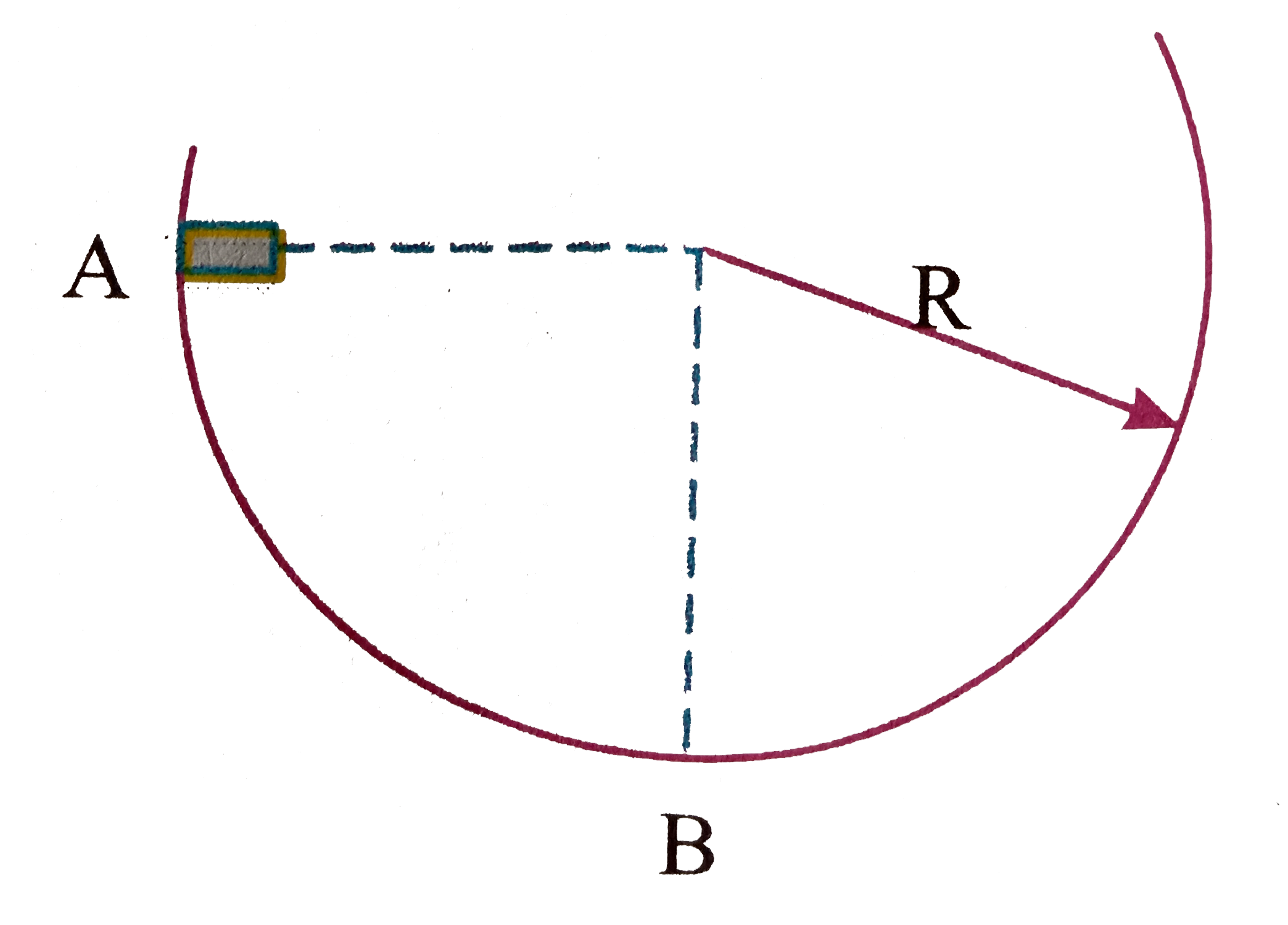 Aacceleration to block is constant throughoutBacceleration of block is g at ACacceleration of block is 3g at BDacceleration of block is 2g at B
Aacceleration to block is constant throughoutBacceleration of block is g at ACacceleration of block is 3g at BDacceleration of block is 2g at BA small body of mass m slides without friction from the top of a hemisphere of radius r. At what height will the body be detached from the surface of hemisphere?
 A32rB23rC12gt2Dv22g
A32rB23rC12gt2Dv22g
Find the gravitational potential due to a hemispherical cup of mass M and radius R, at its centre of curvature.
View SolutionA small sphere S of radius ,r and mass m rolls without slipping, inside a large hemispherical bowl B of radius R as shown in figure. S starts from rest at the top point of the hemisphere
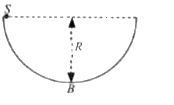
View SolutionA small sphere D of mass and radius rols without slipping inside a large fixed hemispherical radius R(>>r) as shown in figure. If the sphere starts from rest at the top point of the hemisphere normal force exerted by the small sphere on the hemisphere when its is at the bottom B of the hemisphere.
 .
.
View SolutionFor a block of mass m to slide without friction up the rise of height h shown, it must have a minimum initial speed of:
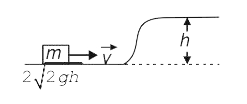
View SolutionA small body of mass m can slide without friction along a through bent which is in the form of a semi-circular arc of radius R. At what height h will the body be at rest with respect to the trough, if the trough rotates with uniform angular velocity ω about a vertical axis:

View Solution
