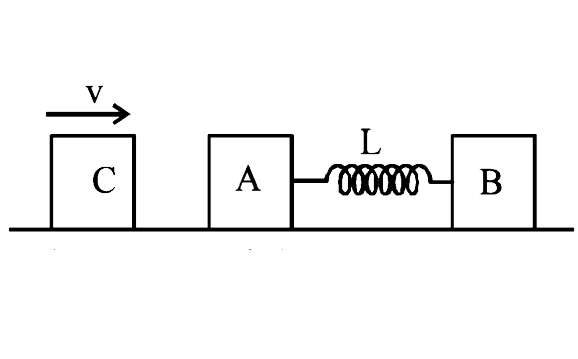
Two blocks A and B, each of mass m, are connected by a masslesss spring of natural length L and spring constant K. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown in fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B, and collides elastically with A. Then, maximum compression of the spring is
v√m2k
m√v2k
√mvk
mv2k
The correct Answer is:A

Initial momentum of the system (block C) =mv
After striking with A, the block C comes to rest and now both blocl AandB moves with velocity momentum V, when compression in spring is maximum .
By the law of the conservation of linear momentum
mv=(m+m)V⇒V=v2
By the law conservation of energy
KE, of block C = K.E, of system + PE of system
12mv2=12(2m)V2=12kx2
12mv2=12(2m)(v2)2+12kx2
⇒kx2=12mv2
⇒x=v√m2k.
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Mechanical Power
Explore 25 Videos
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Circular Motion In Vertical Plane
Explore 21 Videos
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Potential Energy, Conservative And Non-Conservative Forces
Explore 28 Videos
- WAVES AND ACOUSTICSBook:A2ZChapter:WAVES AND ACOUSTICSExercise:Chapter Test
Explore 30 Videos
Similar Questions
Two blocks A and B each of mass m are connected by a light spring of natural length L and spring constant k. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A to B and collides with A. Collision is elastic and head on. Then -

View SolutionTwo blocks A and B each of mass m are connected by a massless spring of natural length L and spring constant k. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length. A third identical block C also of mass m moves on the floor with a speed v along the line joining A and B and collides with A. Then
The kinetic energy of the A-B system at maximum compression of the spring is mv2/4
The maximum compression of the spring v√m/3k<br>Thek∈etice≠rgyoftheA−Bsystematmaxiμmcompression<br>Themaxiμmcoppressionofthespr∈gisvsqrt(m//k)
View Solution
Knowledge Check
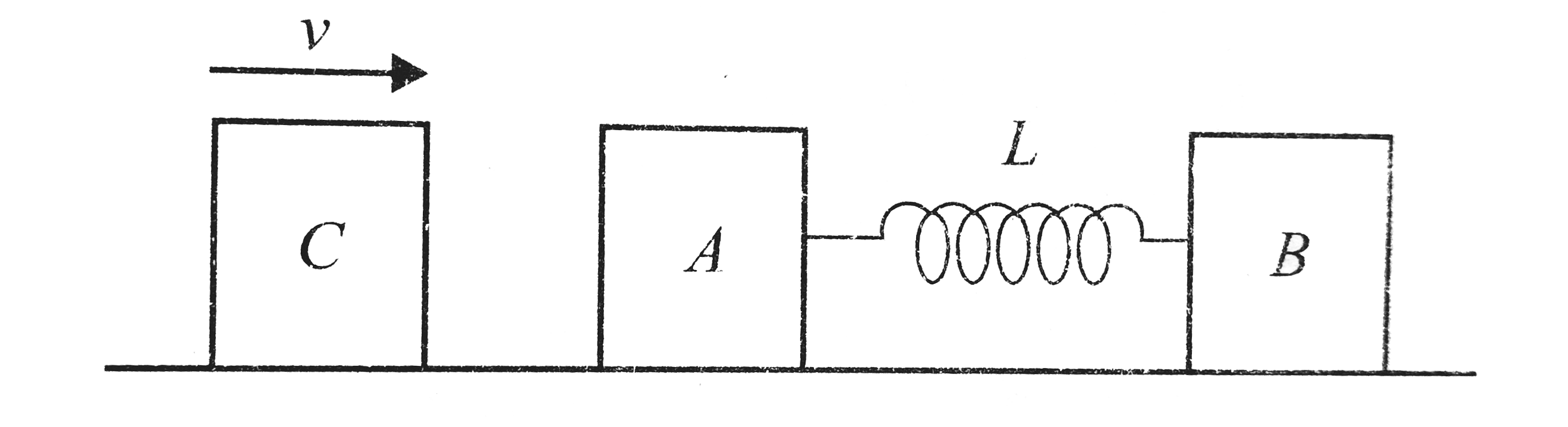
Two blocks A and H. each of mass m, are connected by a massless spring of natural length I. and spring constant K. The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B. and collides elastically with A. Then
 Athe kinetic energy of the A−B system, at maximum compression of the spring, is zero.Bthe kinetic energy of the A−B system, at maximum compression of the spring, isCthe maximum compression of the spring is √(mK)Dthe maximum compression of the spring is v√(m2K)
Athe kinetic energy of the A−B system, at maximum compression of the spring, is zero.Bthe kinetic energy of the A−B system, at maximum compression of the spring, isCthe maximum compression of the spring is √(mK)Dthe maximum compression of the spring is v√(m2K)Two identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
Av√m2kBv√v2kC√mvkDmv2kTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
Av√m2kBm√m2kC√mvkDmv2k
Two blocks A and B of masses m and 2m are connected by a massless spring of natural length L and spring constant k. The blocks are intially resting on a smooth horizontal floor with the spring at its natural length , as shown . A third identical block C of mass m moves on the floor with a speed v0 along the line joining A and B and collides elastically with A. FInd (a) the velocity of c.m. of system (blockA+B+spring) and (b) the minimum compression of spring.

View SolutionTwo identical blocks A and B each of mass m resting on the smooth horizontal floor are connected by a light spring of natural length L and spring constant K. A third block Cof mass m moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
View SolutionA block of mass m is connected to another block of mass M by a massless spring of spring constant k. the blocks are kept of a smooth horizontal plane and are at rest. The spring is unstretched when a constant force F starts acting on the block of mass M of pull it. Find the maximum extension of the spring
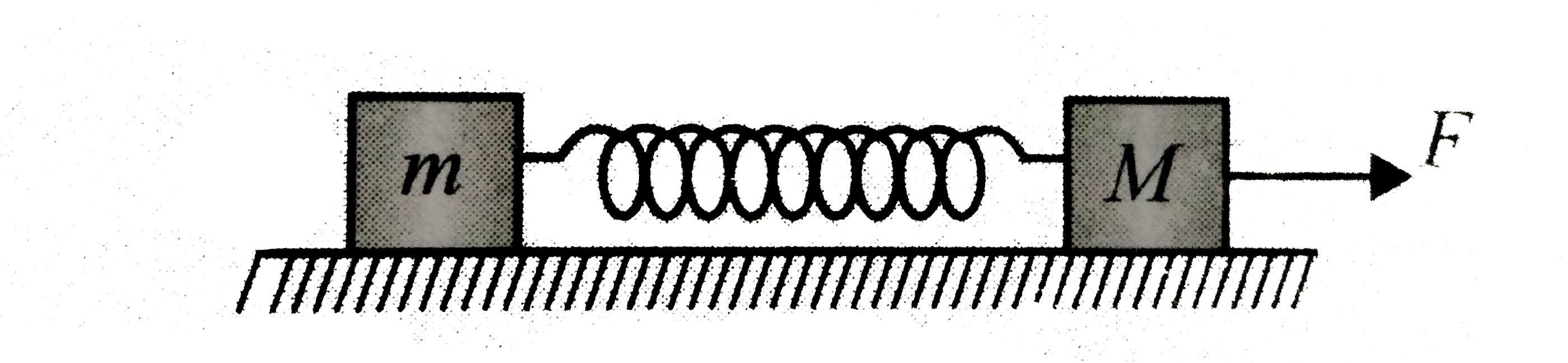
View SolutionTwo blocks A and B, each of mass m, are connected by a spring of force constant K. Initially, the spring is in its natural length. A horizontal constant force F starts acting on block A at time t=0 and at time t , the extension in the spring is seen to be l. What is the displacement of the block A in time t ?
View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View Solution

