Concerete block of mass mAandmB. The gravitutional potential energy of each system is zero at the equilibrium position of the springs. Which ststement is true for the total machanical energy of the springs. Which system when the block , are balanced on the springs?
EA=EB
EA=2EB
EA=4EB
EA=−2EB
The correct Answer is:C
KxA=mAg
KxB=mBg⇒xAxB=mAmB=2⇒xA=2xB
PEA=12Kx2APEB=Kx2B⇒PEAPEB=(xAxB)2=4
So for A, potential energy of spring is four times that for B.
So EA=4EB
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Mechanical Power
Explore 25 Videos
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Circular Motion In Vertical Plane
Explore 21 Videos
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Potential Energy, Conservative And Non-Conservative Forces
Explore 28 Videos
- WAVES AND ACOUSTICSBook:A2ZChapter:WAVES AND ACOUSTICSExercise:Chapter Test
Explore 30 Videos
Similar Questions
The block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View Solution
Knowledge Check
Concrete blocks of masses mA and mB are balanced on two identical vertical springs mA=2mB . The gravitational potential energy of each system is zero at the equilibrium position of the springs. Which statements is true for the total mechanical energy of the systems when the blocks are balanced on the springs?
AEA=EBBEA=2EBCEA=4EBDEA=−2EBA rod mass (M) hinged at (O) is kept in equilibrium with a spring of stiffness (k) as shown in figure. The potential energy stored in the spring is .
 A(mg)24kB(mg)22kC(mg)28kD(mg)2k.
A(mg)24kB(mg)22kC(mg)28kD(mg)2k.
A block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View SolutionFind the elastic potential energy stored in each spring shown in figure, when the block is in equilibrium. Also find the time period of vertical oscillation of the block.

View SolutionIn figue k=100Nm−1M=1kgandF=10N. a. Find the compression of the spring in the equilibrium position. b. A sharp blow by some xternal agent imparts a speed of 2ms−1 to the block towards left. Find the sum of the potential energy of the spring and the kinetic energy of the block at ths instant. c. find the time period of the resulting simple harmonic motion. d. Find the ampitude. e. Write the potential energy of the spring when the block is at the left extreme. f. Write teh potential energy of the spring when teh block is at the right extreme.
The anwer of b, e, and f are different. Explain why this does not violate the principle of conservation of energy.
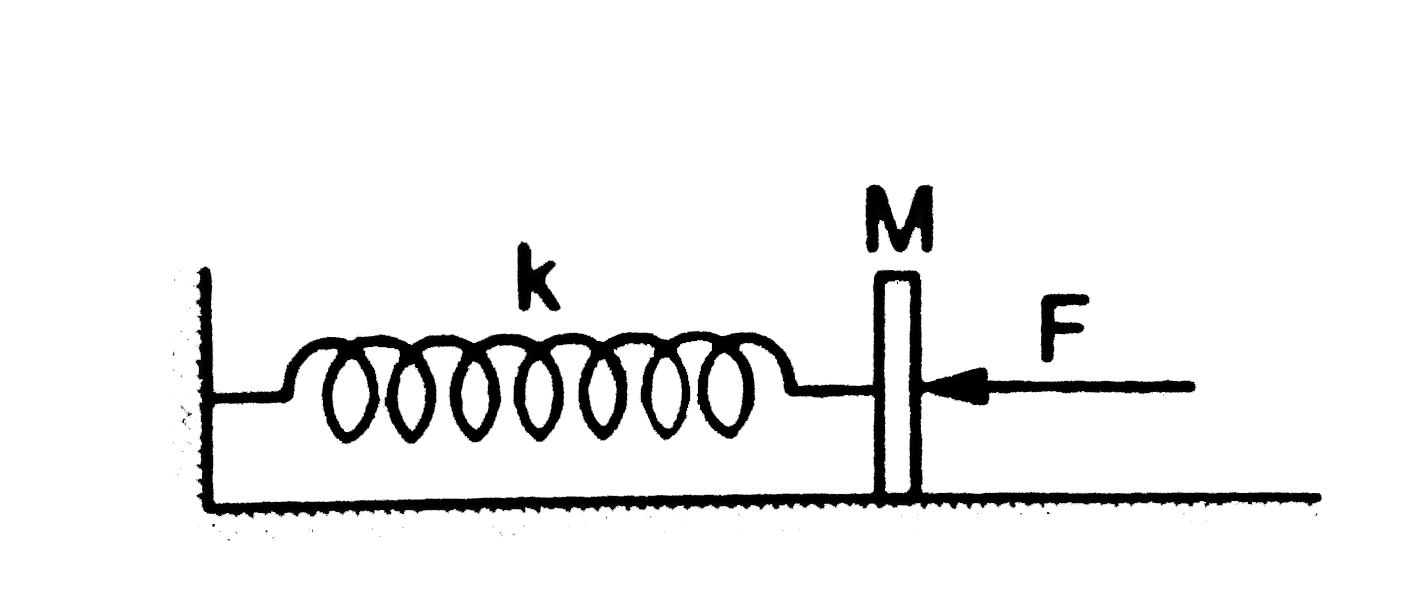
View SolutionIn figure, k=100N/m,M=1kg and F=10N

(a) Find the compression of the spring in the equilibrium position
(b) A sharp blow by some external agent imparts a speed of 2m/s to the block towards left. Find the sum of the potential energy of the spring and the kinetic energy of the block at this instant.
(c) Find the time period of the resulting simple harmonic motion.
(d) Find the amplitude.
(e) Write the potential energy of the spring when the block is at the left estreme.
(f) Write the potential energy of the spring when the block is at the right extreme.
The answers of (b), (e) and (f) are different. Explain why this does not violate the principle of conservation of energy ?
View SolutionFind the mechanical energy of a block-spring system with a spring constant of 1.8 N/cm and an amplitude of 2.4cm.
View SolutionIn figure, the stiffness of the spring is k and mass of the block is m. The pulley is fixed. Initially, the block m is held such that the elongation in the spring is zero and then released from rest. Find:
a. the maximum elongation in the spring.
b. the maximum speed of the block m. Neglect the mass of the spring and that of the string. Also neglect the friction.
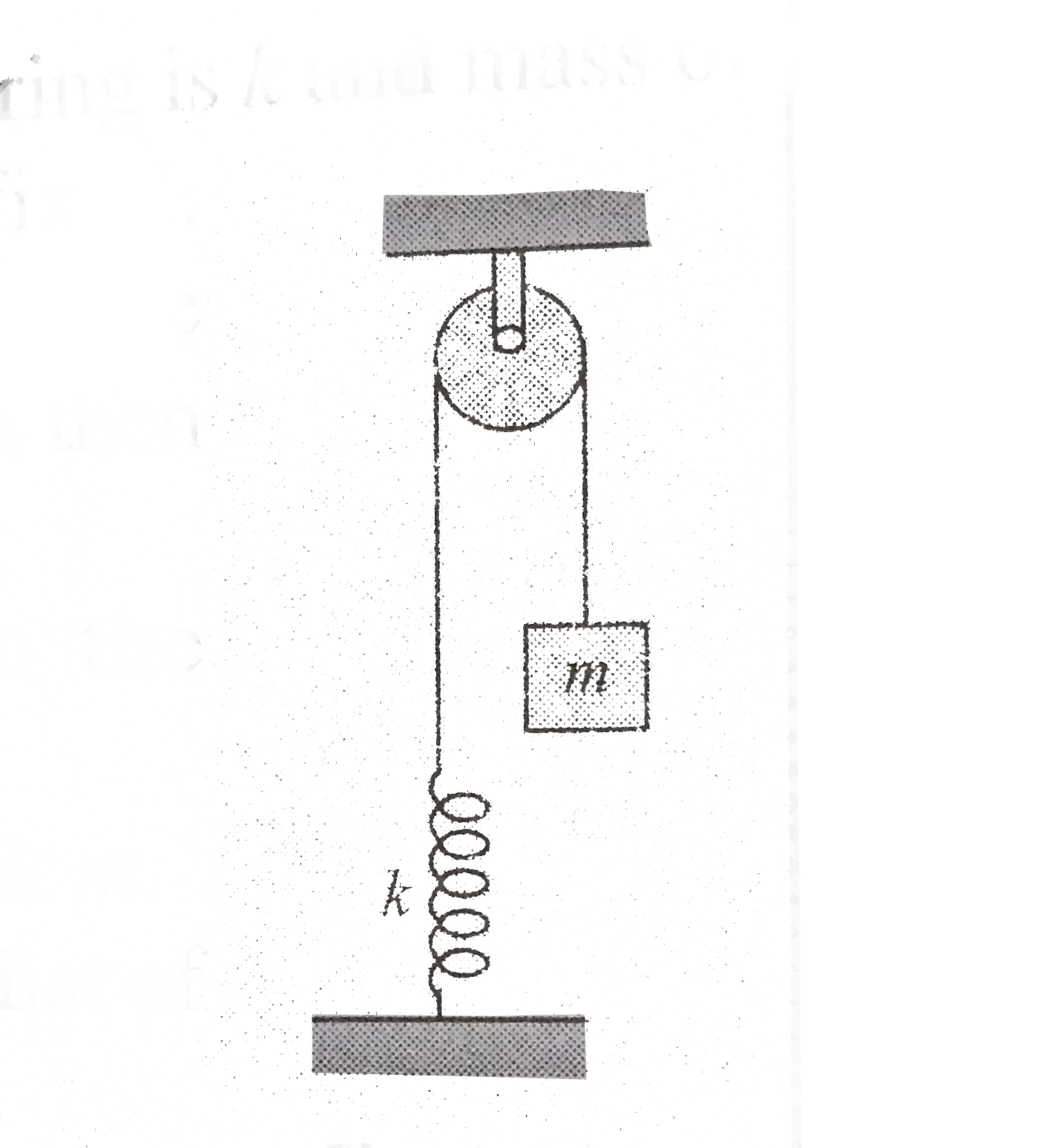
View Solution

