A train stopping at two stations 2km apart on a straight line takes 4 minutes for the journey. Assuming that its motion its uniformly accelerated and then unoformly retarded. If 1x+1y=n, where 'x' and 'y' are the magnitudesof the acceleration and retardation respectively. find the value of n.
2
12
4
14
The correct Answer is:C
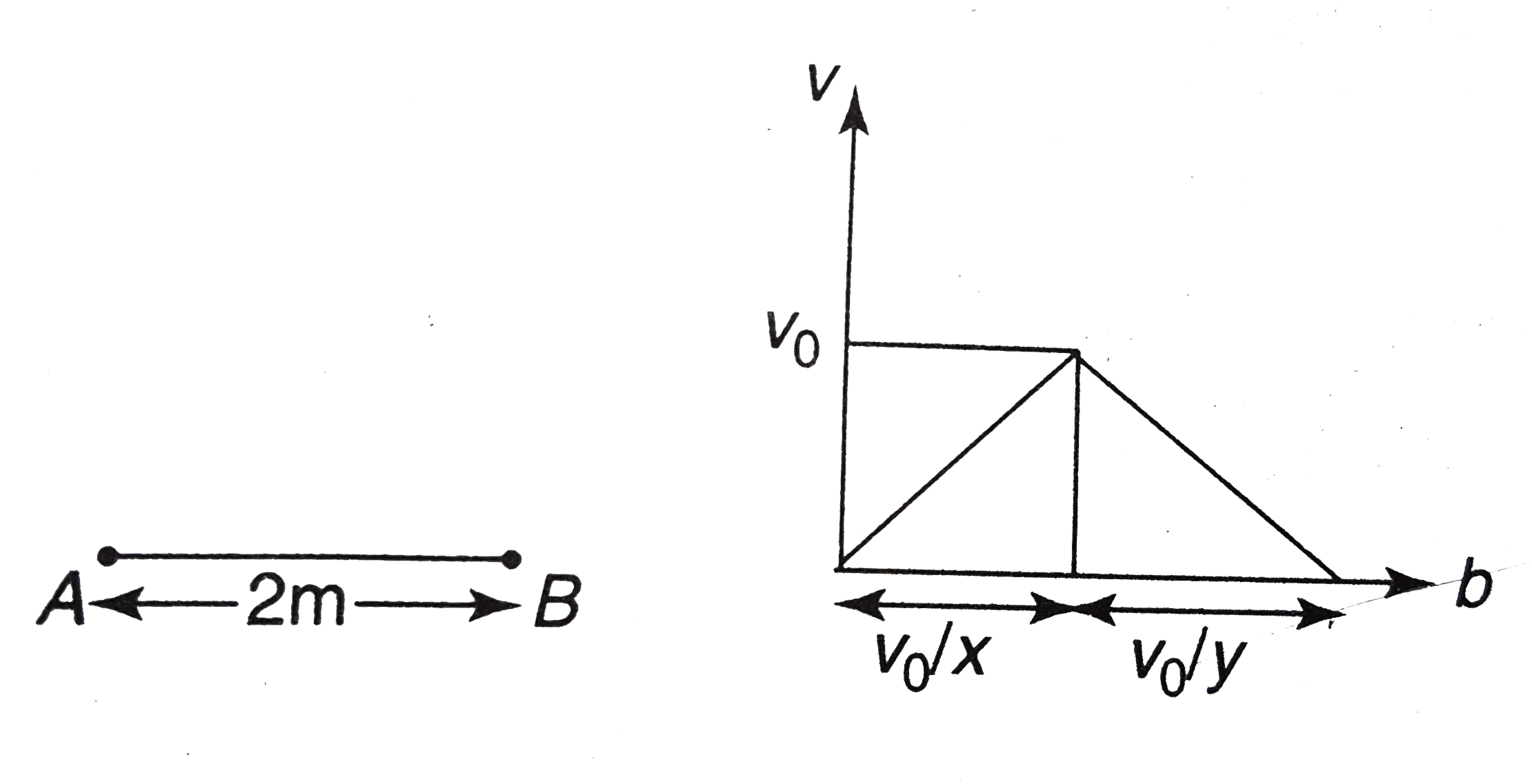
Total time taken =4min
(i) v0x+v0y=4min
(ii) Total distance travelled =2km
⇒ Area under v−t graph =2km
12×v0x×v0+12×v0y×v0=2km
From (i) and (ii), 1x+1y=4.
Topper's Solved these Questions
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBOOK - A2ZCHAPTER - GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONEXERCISE - AIIMS Questions
20 Videos
- FLUID MECHANICSBOOK - A2ZCHAPTER - FLUID MECHANICSEXERCISE - Chapter Test
29 Videos
- GRAVITATIONBOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Chapter Test
29 Videos
Similar Questions
A train stopping at two stations 4 km apart takes 4 min on the journey from one of the station to the other. Assuming that it first accelerates with a uniform acceleration x and then that of uniform retardation y, prove that 1x+1y=2.
View SolutionThe first three terms in the Binomial expansion of (x+y)n are 1,56 and 1372 respectively . Find the value of x and y
View Solution
Knowledge Check
For 1/m of the distance between two stations a train is uniformly accelerated and for 1/n of the distance it is uniformly retarded. It starts from rest at one station and comes to rest at the other. Then the ratio of its greatest velocity to its average velocity is
A1+1/m:1/nB1+1/m+1/n:1C1+1/n:1/mDNone of theseFor 1m of the distance between two stations a train is uniformly accelerated and 1n of the distance it is uniformly retarded. It starts from rest at one station and comes to rest at the other. The ratio of the greatest velocity to the average velocity will be:
A(1+1m−1n)B(1+1m+1n)C(1m+1n−1)D(1m+1n)Starting at time t = 0 from the origin with speed 1ms−1 , a particle follows a tow - dimensional trajectory in the x - y plane so that its coordinates are related by the equation y=x22 . The x and y components of its acceleration are denoted by ax and ay respectively . Then, the incorrect statement is:
Aax=1ms−2 implies that when the particle is at the origin ay=1ms−2Bax=0 implies ay=1ms−2 at all timesCat t=0 the paritcles velcoity points in the x - directionDax=0 implies that at 1 = 1s the angle between the particle 's velocity and the x aixs is 45∘
A train travels in 3 minutes a distance of 3.15 km from rest at one station to rest at another station. It is uniformly accelerated for the 1st 30 seconds and uniformly retarded for the last 15 seconds, the speed being constant for the remaining time. Find the maximum velocity, acceleration and retardation. Use v-t graph to solve th problem.
View SolutionA train takes t seconds to perform a journey. It travels for t/n seconds with uniform acceleration, then for time (n−3)t/n with uniform speed v and finally for 2t/n seconds with uniform retardation. Then the average speed is ..........
View SolutionIf (1+by)n=(1+8y+24y2+....) where n∈N then the value of b and n are respectively-
View SolutionA particle is moving in a straight line with constant acceleration. Then its acceleration is s−s'm−n where sand s' are the spaces described during the mth and the nth seconds respectively.
View SolutionA Bullet Train in Japan starting from rest accelerates uniformly at 0.5ms−2 for 2 minutes. It then maintains uniform speed for 20 minutes and then retards uniformly at the rate of 0.25ms−1 and comes to rest. Calculate the average speed of the train
View Solution
