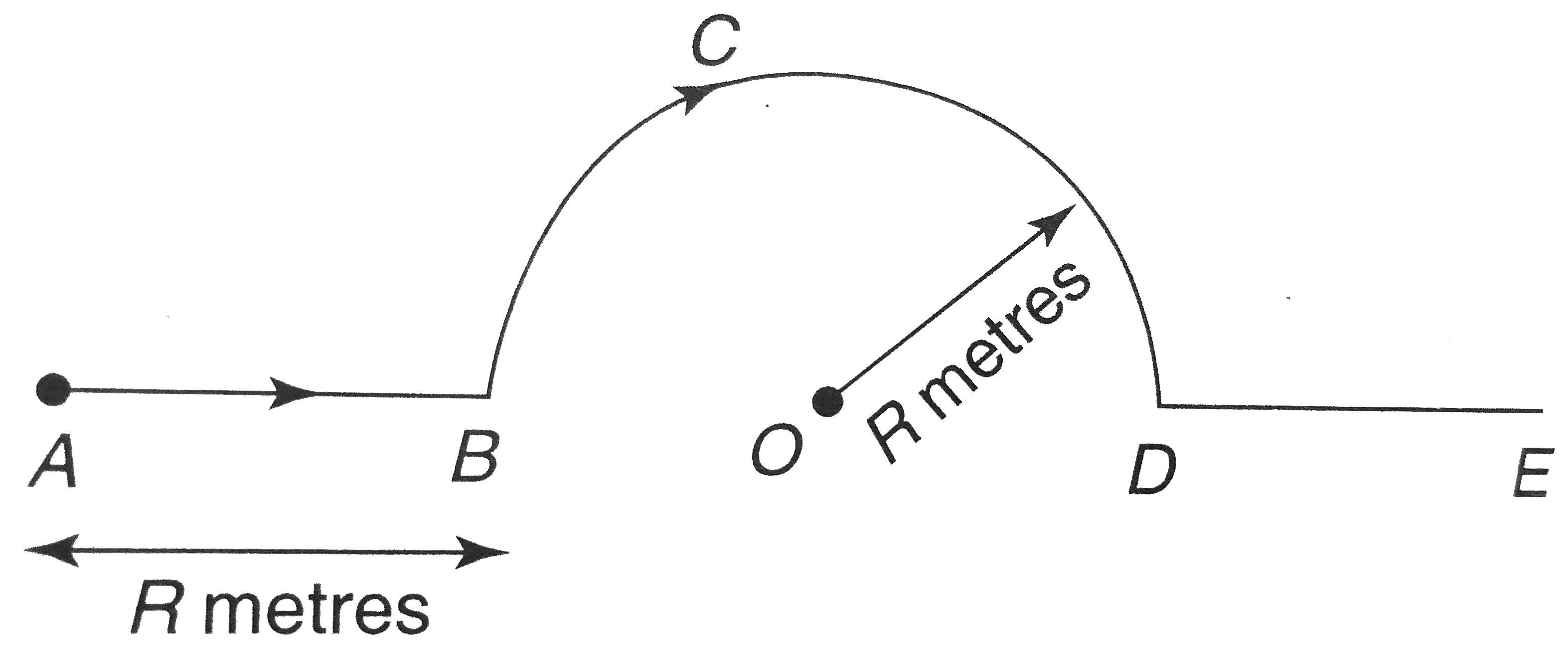
A particle at t=0 second is at point A and moves along the shown path (ABCDF) with uniform speed v=(1+π3)m/s. Both the straight segments AB and DE are along the diameter BD of semicircle BCD radius R=1 meter. Find the instant of time at which the instantaneous velocity of the particle is along the direction of average velocity from t=0 second to that instant.
2 sec
4 sec
1 sec
1.5 sec
The correct Answer is:C
The required condition is achieved when the particle is at P such that AP is tangent to semicircle.
Hence required time =R+Rπ3v=1sec.
Topper's Solved these Questions
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBook:A2ZChapter:GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONExercise:AIIMS Questions
Explore 20 Videos
- FLUID MECHANICSBook:A2ZChapter:FLUID MECHANICSExercise:Chapter Test
Explore 29 Videos
- GRAVITATIONBook:A2ZChapter:GRAVITATIONExercise:Chapter Test
Explore 29 Videos
Similar Questions
Knowledge Check
A particle travels along a semicircle of radius R in 2 s. The velocity of the particle is
AπRBRC2πRD2RA particle travels along a semicircle of radius R in 2 s. The velocity of the particle is
AπRBRC2πRD2RFigure shows the velocity time graph of a particle moving along straight line (v is m/s and t is in second). It average velocity in 20 seconds will be:
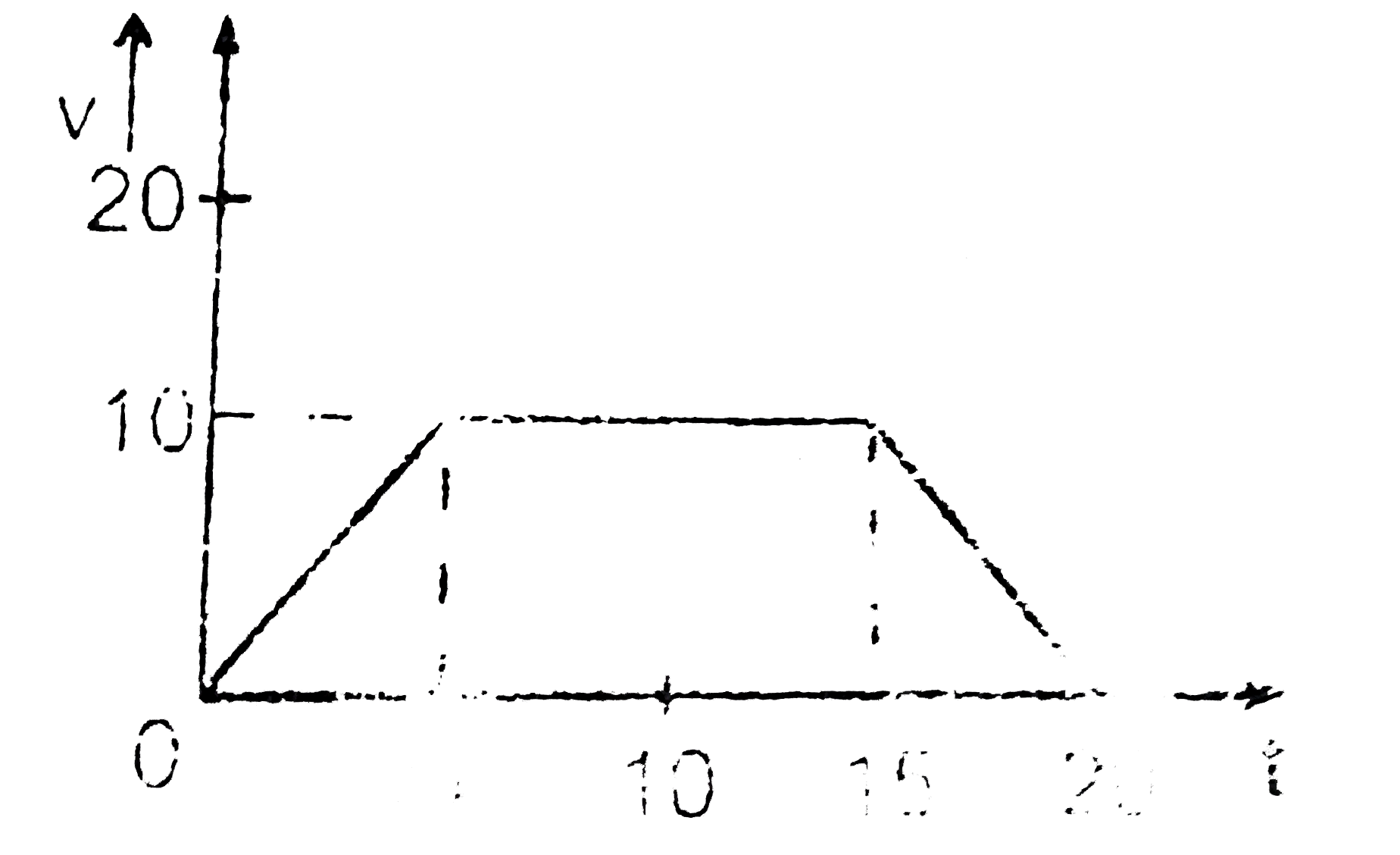 .A10m/sBzeroC3.75m/sD7.5m/s
.A10m/sBzeroC3.75m/sD7.5m/s
A particle moves along a semicircle of radius 10m in 5 seconds. The average velocity of the particle is
View SolutionFor which of the following graphs the average velocity of a particl moving along a straight line for time interval (0,t) must be negative−
View SolutionA particle moves along a semicircular path of radius R in time t with constant speed. For the particle calculate
View SolutionThe velocity of a particle moving with constant acceleration at an instant t0 is 10m/s After 5 seconds of that instant the velocity of the particle is 20m/s. The velocity at 3 second before t0 is:-
View SolutionPosition-time graph for a particle moving along x− direction is as shown in the figure. Average speed of the particle from t=0 to t=4 is :

View Solution


