A stone is dropped from the top of a tower. When it crosses a point 5 m below the top, another stone is let fall from a point 25 m below the top. Both stones reach the bottom of the tower simultaneously. Find the height of the tower. Take g=10m/s2.
45 m
50 m
60 m
65 m
The correct Answer is:A
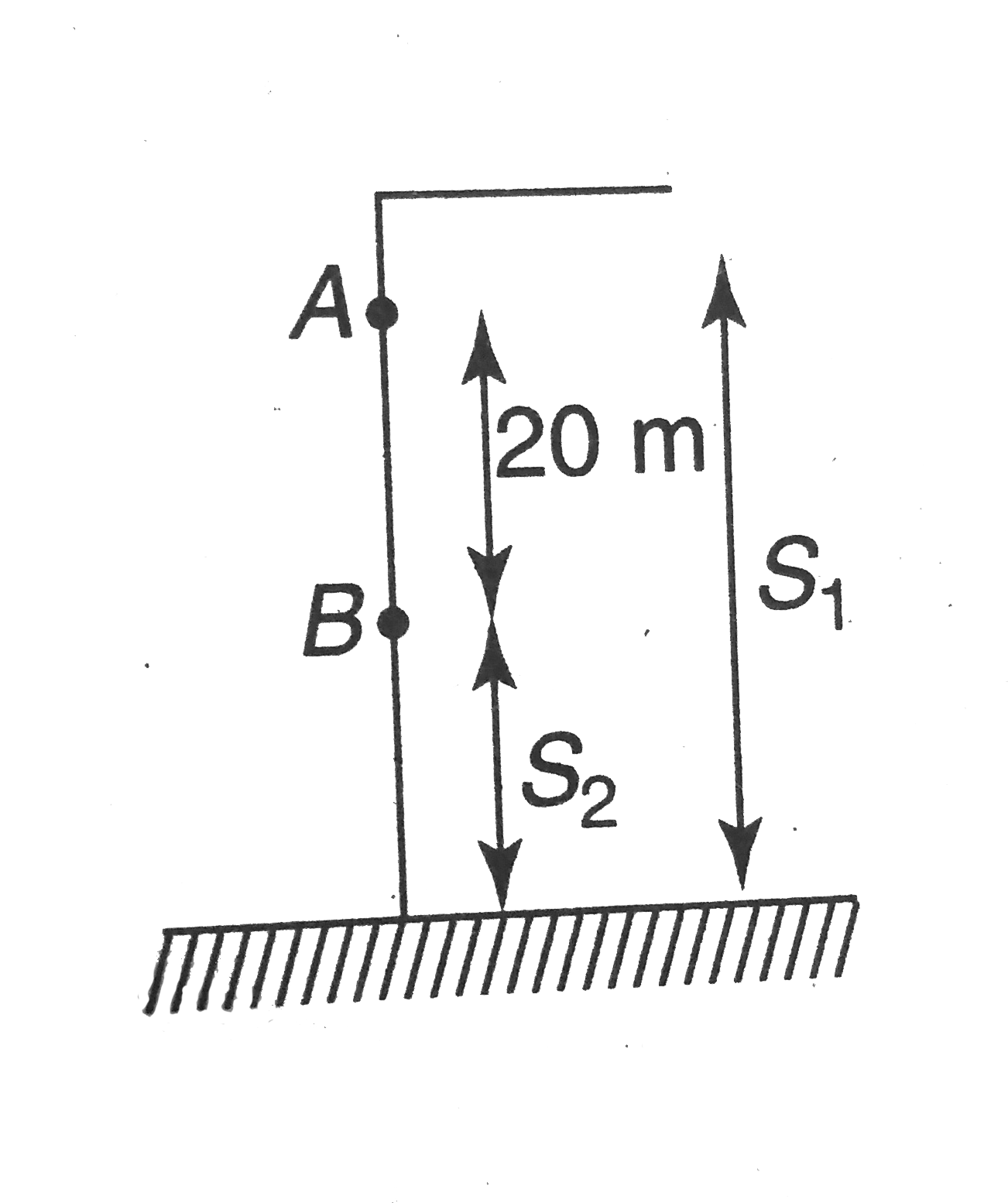
Velocity of 1st stone when passing at A
V2=0+2.10.5⇒V=10m/s
And S1−S2=20m
⇒(10.t+1210.t2)−(12.10.t2)=20
At t=2s,S2=12gt2=12×10×22=20m
Hence height of the tower,
H=S1+S2=25+20=45m.
Topper's Solved these Questions
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBOOK - A2ZCHAPTER - GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONEXERCISE - AIIMS Questions
20 Videos
- FLUID MECHANICSBOOK - A2ZCHAPTER - FLUID MECHANICSEXERCISE - Chapter Test
29 Videos
- GRAVITATIONBOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Chapter Test
29 Videos
Similar Questions
.A stone is dropped from the top of a building.When it crosses a point 5m .below the top,another stone starts to fall from a point 25m below the top.Both stones reach the bottom of building simultaneously. The height of the building is
View SolutionA particle is dropped from the top of a tower. When it has travelled a distance of 5m , another particle is dropped from a distance of 25m below the top of tower. If both of them reach the bottom of tower simultaneously, then find the height of tower.
View Solution
Knowledge Check
A stone is dropped from the top of tower. When it has fallen by 5m from the top, another stone is dropped from a point 25m below the top. If both stones reach the ground at the moment, then height of the tower from grounds is : (take g=10m/s2)
A45mB50mC60mD65mA stone is dropped from the top of a tower of height h. Aftre 1s another stone is droppped from the balcony 20m below the top. Both reach the bottom simultaneously. What is the value of h ? Take g=10ms−2.
A315mB312.5mC3125mD25,31A stone dropped from the top of a tower reaches the ground in 3 s. The height of the tower is
A18.6 mB39.2 mC44.1 mD98 m
A stone is dropped from the top of tall tower and one second later another stone is dropped from a balcany 20 m below the top . If both the stones reach the ground at the same instant , determine the height of the tower .take g=10ms−2
View SolutionA stone is falling from the top of a vertical tower, when it has ascended a meters, another stone is let fall from a point x meters below the top. If they fall from rest and reach the ground together, then show that the height of the tower is (a+x)2/a meters.
View SolutionA particle is dropped from the top of a tower. It covers 40 m in last 2s. Find the height of the tower.
View SolutionA stone is dropped from the top of a tower. If it hits the ground after 10 seconds, what is the height of the tower?
View SolutionA stone dropped from the top of the tower touches the ground in 4 sec. The height of the tower is about
View Solution
