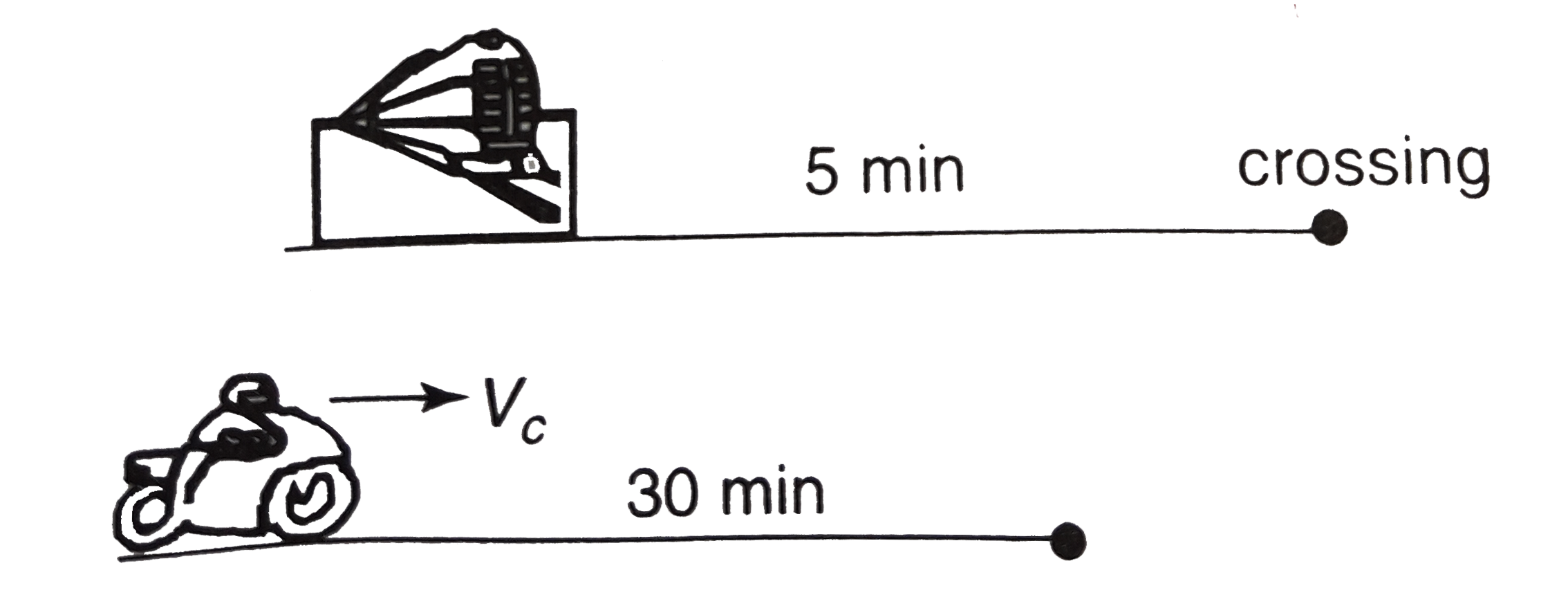
A railway track runs parallel to a road until a turn brings the road to railway crossing. A cyclist rides along the road every day at a constant speed $20 k m / h r$ . He normally meets a train that travels in same direction at the crossing. One day he was late by $25$ minutes and met the train $10 k m$ before the railway crossing. Find the speed of the train.

A

$9 k m / h r$

B

$90 k m / h r$

C

$120 k m / h r$

D

$40 k m / h r$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$t_{cycle} = \frac{10 k m}{20 k m h^{- 1}} = \frac{1}{2} h = 30 min$
$Δ t = 5 min = \frac{5}{60} h r$
Train running as per schedule.
So $v_{train} = \frac{10}{(50 / 60)} = \frac{10 \times 60}{5} = 120 k m h^{- 1}$ .

Updated on:21/07/2023

|

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

A train runs at the speed of 40 km/hr. A man is running at the speed of 25 km/hr parallel of train in the same direction. If train crosses that man in 48 seconds then what is the length of train ?
A100 m
B50 m
C150 m
D200 m s
A train is running at the rate of 40 kmph. A man also is going in the same direction parallel to the train at the speed of 25 kmph. If the train crosses the man in 48 sec, the length of the train is -----
A50 metres
B100 metres
C150 metres
D200 metres
A train 120 metres long travels at 60 km/hr. A man is running at 6 km/h in the same direction in which the train is going. The train will cross man in:
A6 seconds
B7 seconds
C6 seconds
D8 seconds

A2Z-GENERAL KINEMATICS AND MOTION IN ONE DIMENSION-Chapter Test

Home
Ask Doubt
Profile