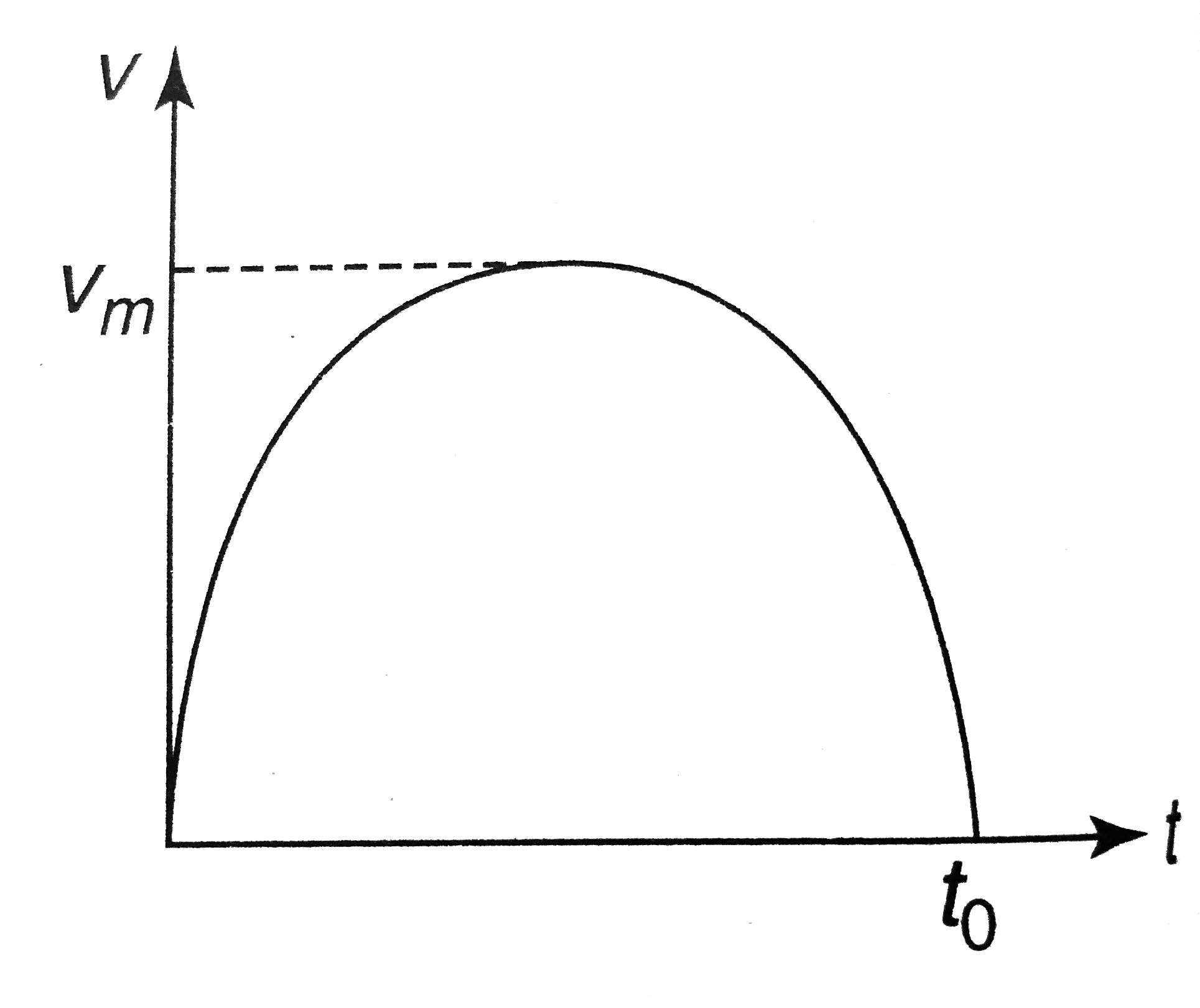
The velocity of a particle moving in a straight line varies with time in such a manner that v versus t graph is represented by one-half of an ellipse. The maximum velocity is vm and the total time of motion is t0
(i) average velocity of the particle is π4vm
(ii) such motion cannot be realized in practical terms.
only (i) is correct
only (ii) is correct
both (ii) and (ii) are correct
both (i) and (ii) are wrong
The correct Answer is:C
The displacement of the particle is determined by the area bounded by the curve, This area is : s=12πvmt02
The average velocity is : <v>=st0=π4vm.
Such motion cannot be realized in practical terms since at the initial and final moments, the acceleration (which is slope of v−t graph) is infinitely large. Hence. both (i) and (ii) are correct, i.e., answer is ( c).
Topper's Solved these Questions
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBook:A2ZChapter:GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONExercise:AIIMS Questions
Explore 20 Videos
- FLUID MECHANICSBook:A2ZChapter:FLUID MECHANICSExercise:Chapter Test
Explore 29 Videos
- GRAVITATIONBook:A2ZChapter:GRAVITATIONExercise:Chapter Test
Explore 29 Videos
Similar Questions
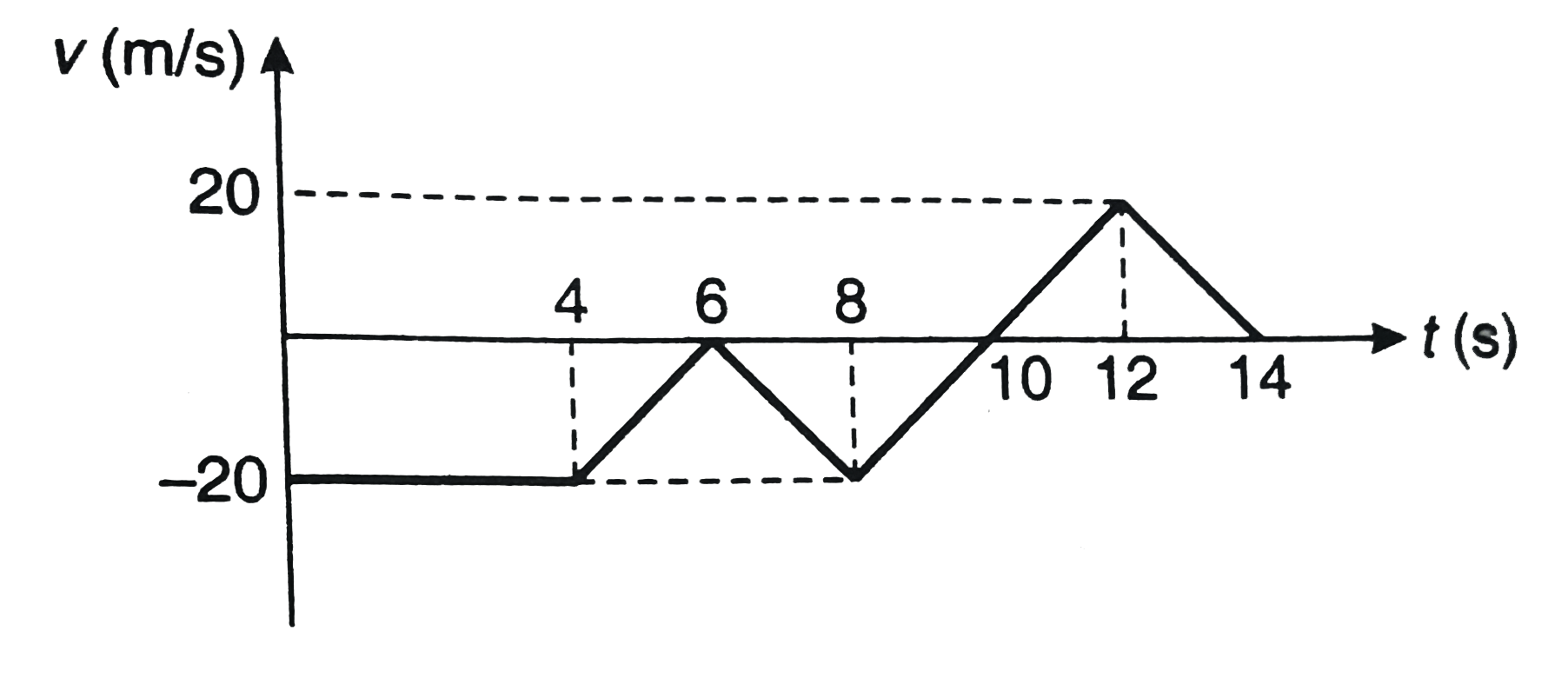
Velocity-time graph of a particle moving in a straight line is shown in figure. At time t=0.s=20m. Plot a-t and s-t graphs of the particle.
View SolutionA particle is moving in a straight line. It covers half of the total distance with velocity v0 Remaining half distance is covered with a velocity v1 for half the time and with velocity v2 for another half of time. Find the average velocity of the particle.
View Solution
Knowledge Check
The acceleration of a particle moving along a straight line at any time t is given by a = 4 - 2v, where v is the speed of particle at any time t The maximum velocity is
A4 m/sB2 m/sC6 m/sDInfinityThe velocity -time (v−t) graph of a particle moving in a straight line is shown in figure. The acceleration of the particle at t=9 is:
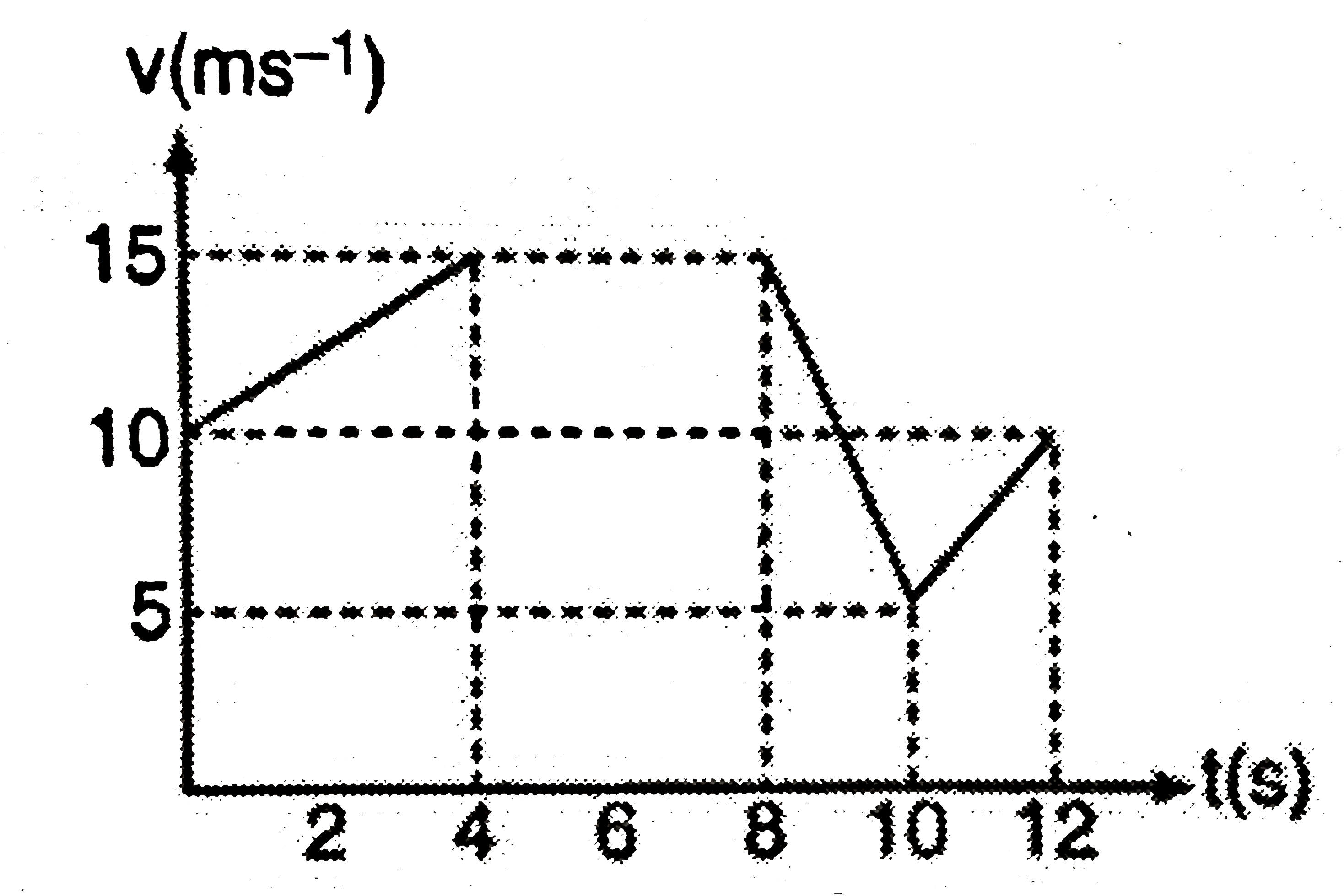 AzeroB5ms−2C−5ms2D−2ms−2
AzeroB5ms−2C−5ms2D−2ms−2The velocity v of a body moving along a straight line varies with time t as v=2t2e−t, where v is in m/s and t is in second. The acceleration of body is zero at t =
A0B2 sC3DBoth (1) & (2)
Velocity of a particle moving in a straight line varies with its displacement as v=(√4+4s)m/s. Displacement of particle at time t=0 is s=0. Find displacement of particle at time t=2s.
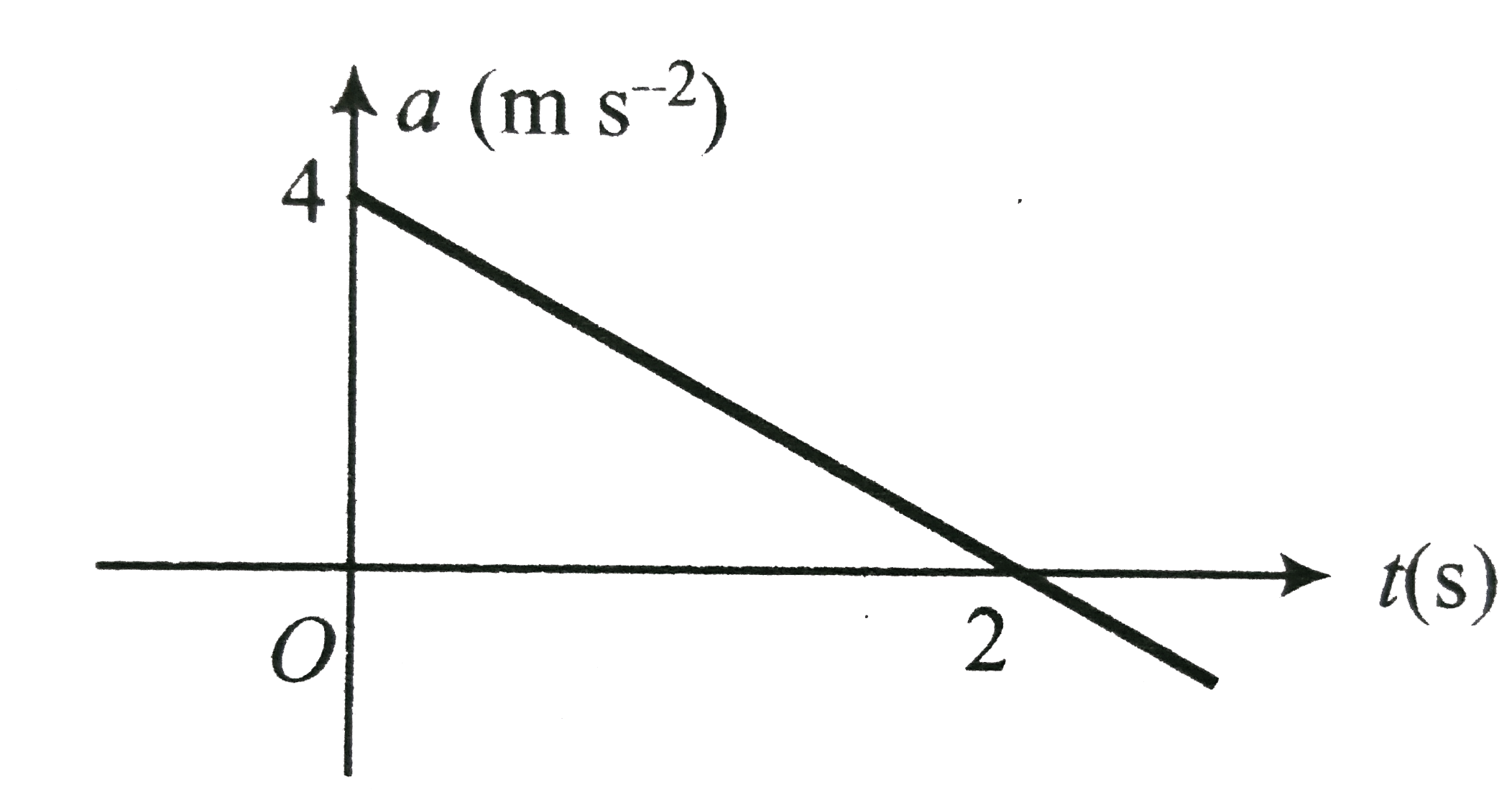
View SolutionThe acceleration versus time graph of a particle moving in a straight line is show in figure. The velocity-time graph of the particle would be
 .
.
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The speed is minimum after t=0 second at instant of time
View SolutionA particle moves along a straight line its velocity dipends on time as v=4t−t2. Then for first 5s:
View SolutionForce acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
View Solution

