Question

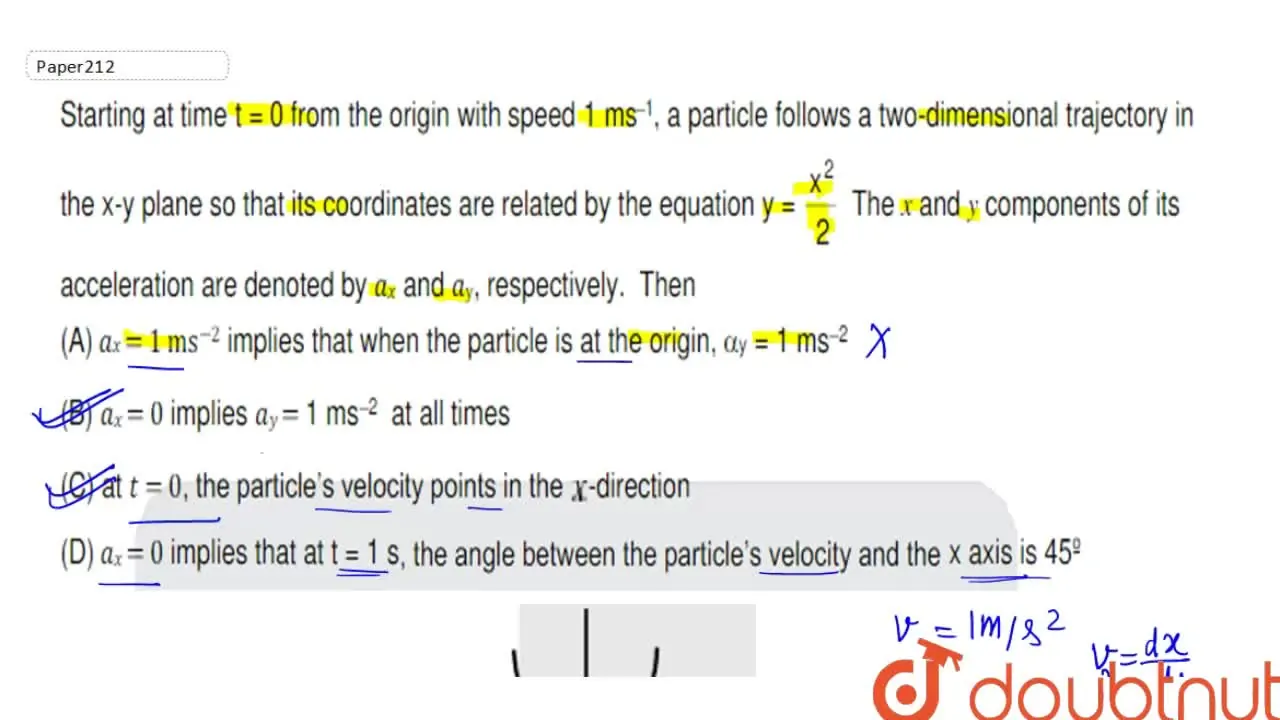
Starting at time t = 0 from the origin with speed $1m{s}^{-1}$ , a particle follows a tow - dimensional trajectory in the x - y plane so that its coordinates are related by the equation $y=\frac{x^2}{2}$ . The x and y components of its acceleration are denoted by $a_x$ and $a_y$ respectively . Then, the incorrect statement is:

Options

A. `a_(x) = 1 ms^(-2)` implies that when the particle is at the origin `a_(y) = 1 ms^(-2)`
B. `a_(x) = 0 ` implies `a_(y) = 1ms^(-2)` at all times
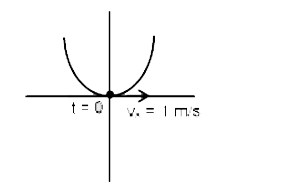
C. at `t = 0 ` the paritcles velcoity points in the x - direction
D. `a_(x) = 0` implies that at 1 = 1s the angle between the particle 's velocity and the x aixs is `45^(@)`

Answer

A

Explanation

To solve the problem, we need to analyze the motion of a particle moving in a two-dimensional plane defined by the equation $$y=\frac{x^2}{2}$$. We will find the relationships between the x and y components of acceleration, $$a_x$$ and $$a_y$$, and determine which statement is incorrect.

Step 1: Understand the trajectory
The trajectory of the particle is given by the equation:
\( y = \frac{x^2}{2} \)
This represents a parabolic path in the x-y plane.

Step 2: Find the velocity components
The velocity components in the x and y directions can be expressed as:
\( v_x = \frac{dx}{dt}, \quad v_y = \frac{dy}{dt} \)
Using the chain rule for differentiation, we can relate \( v_y \) to \( v_x \):
\( v_y = \frac{dy}{dx} \cdot v_x \)
Differentiating \( y = \frac{x^2}{2} \) with respect to \( x \):
\( \frac{dy}{dx} = x \)
Thus, we have:
\( v_y = x v_x \)

Step 3: Find the acceleration components
The acceleration components can be found by differentiating the velocity components:
\( a_x = \frac{dv_x}{dt}, \quad a_y = \frac{dv_y}{dt} \)
Using the product rule for \( v_y \):
\( a_y = \frac{d}{dt}(x v_x) = \frac{dx}{dt} v_x + x \frac{dv_x}{dt} = v_x v_x + x a_x = v_x^2 + x a_x \)

Step 4: Analyze the initial conditions
At \( t = 0 \), the particle starts from the origin (0, 0) with an initial speed of \( 1 \, \text{m/s} \):
\( v_x = 1 \, \text{m/s}, \quad v_y = 0 \, \text{m/s} \quad \text{(since at } x = 0, y = 0\text{)} \)
Thus, at the origin:
\( a_y = v_x^2 + x a_x = 1^2 + 0 \cdot a_x = 1 \, \text{m/s}^2 \)

Step 5: Evaluate the statements
Now we can evaluate the statements given in the problem to determine which one is incorrect based on our findings:
1. If \( a_x = 1 \, \text{m/s}^2 \), then \( a_y \) can be calculated as:
\( a_y = 1 + 0 \cdot 1 = 1 \, \text{m/s}^2 \)
This statement is correct.

2. If \( a_x = 0 \, \text{m/s}^2 \), then:
\( a_y = 1 + 0 \cdot 0 = 1 \, \text{m/s}^2 \)
This statement is also correct.

3. At \( t = 0 \), the particle's velocity along the x direction is \( 1 \, \text{m/s} \) and \( v_y = 0 \, \text{m/s} \). This statement is correct.

4. If \( a_x = 0 \) implies that at \( t = 1 \, \text{s} \), the angle between the particle's velocity and the x-axis is \( 45^\circ \). This statement is incorrect because if \( a_x = 0 \), then \( v_x \) remains constant, and \( v_y \) will not equal \( v_x \) at \( t = 1 \, \text{s} \).

Conclusion
The incorrect statement is:
- If \( a_x = 0 \), then at \( t = 1 \, \text{s} \), the angle between the particle's velocity and the x-axis is \( 45^\circ \).