A rod of mass m and length L , pivoted at one of its ends, is hanging vertically . A bullet of the same mass moving at speed v strikes the rod horizontally a a distance x from its pivoted end and gets embedded in it. The combined system now rolates with rotates with angular speed ω about the pivot . The maximum angular speed ωM is achieved for x=xm . Then .
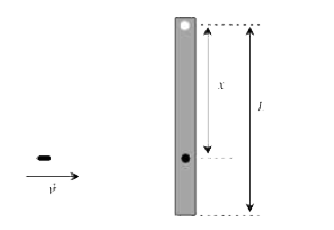
ω=3vxL2+3x2
ω=12vxL2+12x2
xM=1√3
ωM=v2L√3
The correct Answer is:A,C,D
From angular momentum conservation
mvx=(ML23+mx2)ω
ω=3vxL2+3x2
For maximum angular velocity
dωdx=0
ddx(L2x+3x)=0,−L2x2+3=0,x=L√3
ωmax=√3v2L
Topper's Solved these Questions
- JEE (ADVANCE) 2020Book:JEE ADVANCED PREVIOUS YEARChapter:JEE (ADVANCE) 2020Exercise:SECTION 3
Explore 6 Videos
- JEE (ADVANCE) 2020Book:JEE ADVANCED PREVIOUS YEARChapter:JEE (ADVANCE) 2020Exercise:SECTION 3
Explore 6 Videos
- JEE ADVANCEDBook:JEE ADVANCED PREVIOUS YEARChapter:JEE ADVANCEDExercise:PHYSICS SECTION - IV Matrix Match Type
Explore 2 Videos
Similar Questions
A rod of mass m and length l hinged at the centre is placed on a horizontal surface. A bullet of mass m moving with velocity v strikes the end. A of the rod and gets embedded in it. The angular velocity with which the systems rotates about its centre of mass after the bullet strikes the rod

View SolutionA rod of mass M and length L is kept on a frictionless horizontal floor. A particle of mass m moving perpendicular to the rod with a speed v strikes at the end of the rod and sticks there. Calculate angular velocity acquired by the combined system.
View Solution
Knowledge Check
A unifrom rod of mass m and length l0 is pivoted at one end and is hanging in the vertical at one end and is hagingh in the vertical direction.The period of small angular oscillations of the rod is
 AT=3π√2l03gBT=4π√l03gCT=4π√2l03gDT=2π√2l03g
AT=3π√2l03gBT=4π√l03gCT=4π√2l03gDT=2π√2l03gA uniform rod smoothly pivoted at one of its ends is released from rest. If it swings in vertical plane, the maximum speed of the end P of the rod is.
 .A2√3glB√3glC2√2glD√gl
.A2√3glB√3glC2√2glD√glA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]
A rigid rod of mass m & length l is pivoted at one of its ends. If it is released from its horizontal position, find the speed of the centre of mass of the rod when it becomes vertical.
View SolutionA thin rod of mass m and length l is hinged at the lower end to a level floor and stands vertically. Then its upper end will strike the floor with a velocity given by:
View SolutionA bullet of mass m moving with a speed v strikes a wooden block of mass M & gets embedded into the block. The final speed is
View SolutionConsider a rod of mass M and length L pivoted at its centre is free to rotate in a vertical position plane. The rod is at rest in the vertical position. A bullet of mass M moving horizontally at a speed v strikes and embedded in one end of the rod. The angular velocity of the rod just after the collision will be.
View SolutionA rod of mass 4m and length L is hinged at the mid point. A ball of mass 'm' moving with speed V in the plane of rod, strikes at the end at an angle of 45∘ and sticks to it. The angular velocity of system after collision is-
View Solution