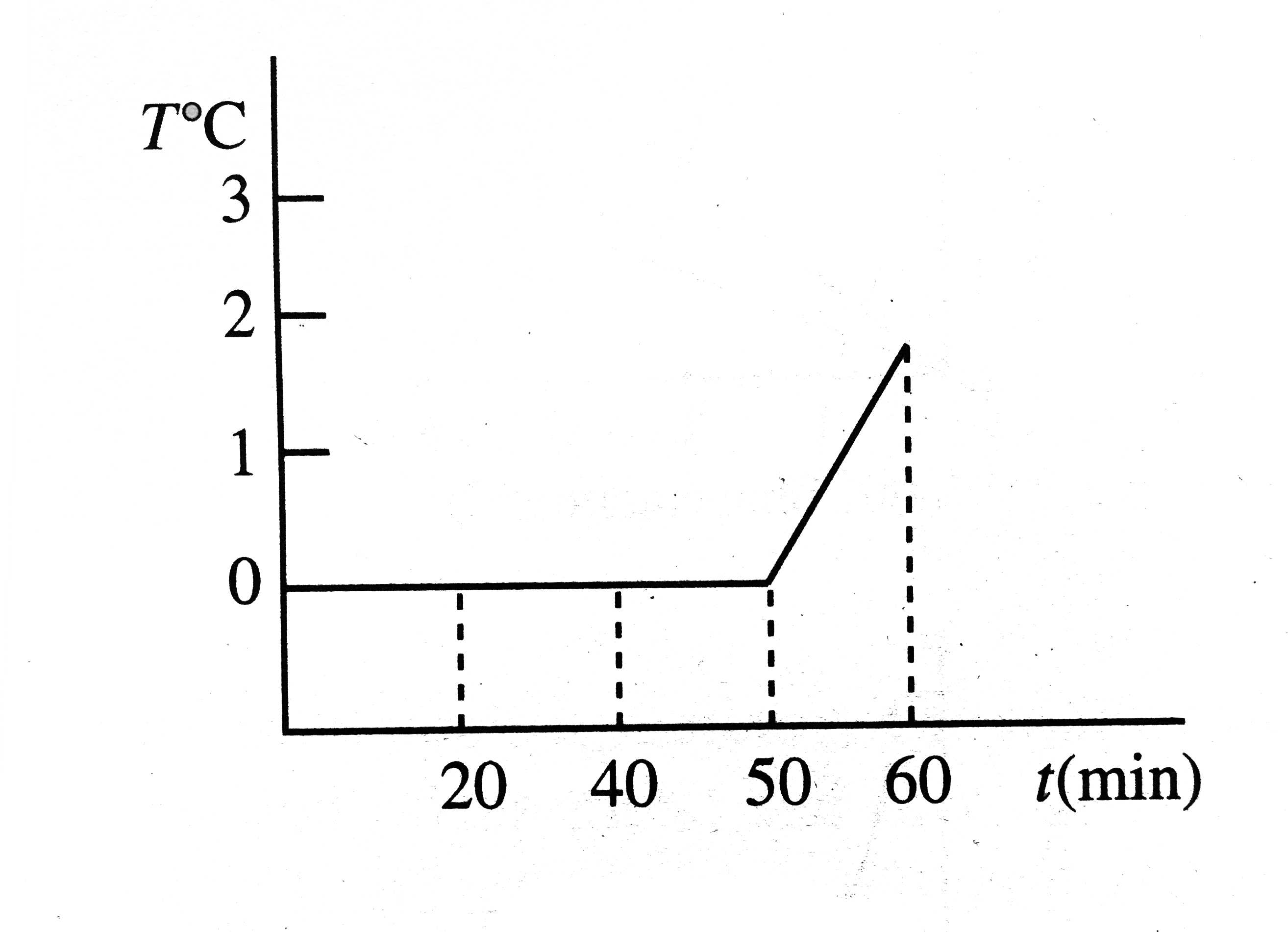
A cooking vessel on a slow burner contains 5 kg of water and an unknown mass of ice in equilibrium at 0^@C at time t=0. The temperature of the mixture is measured at various times and the result is plotted as shown in Fig. During the first 50 min the mixture remains at 0^@C. From 50 min to 60 min, the temperature increases to 2^@C Neglecting the heat capacity of the vessel, the initial mass of the ice is
A cooking vessel on a slow burner contains 5 kg of water and an unknown mass of ice in equilibrium at 0∘C at time t=0. The temperature of the mixture is measured at various times and the result is plotted as shown in Fig. During the first 50 min the mixture remains at 0∘C. From 50 min to 60 min, the temperature increases to 2∘C Neglecting the heat capacity of the vessel, the initial mass of the ice is

A

107kg

B

57kg

C

54kg

D

58kg

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B

Let m be the mass of ice.
Rate of heat given by the burner is constant.
In the first 50 min
dQdt=mLt1=mkg×(80×4.2×103)J/kg(50min) .(i)
From 50 min to 60 min
dQdt=(m+5)SH2OΔθt2
=(m+5)kg(4.2×103)J/kg×2∘C10min ..(ii)
From Eqs. (i) and (ii)
80m50=2(m+5)10
7m=5⇒m=57kg=0.7kg

Updated on:21/07/2023
|
Class 11PHYSICSTHERMAL EXPANSION AND CALORIMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • 5 g of ice at 0∘C and 20 g of water at 45∘C are mixed. The temperature of the mixture will be

    A10∘C
    B20∘C
    C30∘C
    D40∘C

  • One gram of ice at 0∘C is added to 5 gram of water at 10∘C. If the latent heat of ice be 80 cal/g, then the final temperature of the mixture is -

    A5∘C
    B0∘C
    C−5∘C
    DNone of the above

  • 100g ice at 0∘C is mixed with 100g water at 100∘C. The resultant temperature of the mixture is

    A10∘C
    B20∘C
    C30∘C
    D40∘C