A thermally isulated piece of metal is heated under atmospheric pressure by an electric current so that it receives electric energy at a constant power P. This leads to an increase of absolute temperature T of the metal with time t as follows:
. Here, a, and are constants. The heat capacity of the metal is
The correct Answer is:B
Heat given to the metal
..(i)
At constant pressure in time interval at
Given
..(ii)
From Eqs. (i) and (ii)
Topper's Solved these Questions
- CALORIMETRYBook:CENGAGE PHYSICSChapter:CALORIMETRYExercise:Multiple Correct
Explore 25 Videos
- CALORIMETRYBook:CENGAGE PHYSICSChapter:CALORIMETRYExercise:Comprehension
Explore 30 Videos
- CALORIMETRYBook:CENGAGE PHYSICSChapter:CALORIMETRYExercise:Subjective
Explore 25 Videos
- BASIC MATHEMATICSBook:CENGAGE PHYSICSChapter:BASIC MATHEMATICSExercise:Exercise 2.6
Explore 20 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
The molar heat capacity of a perfect gas at constant volume is Cv. The gas is subjected to a process T=T0eAV, Where T0 and A are constant. Calculate the molar heat capacity of the gas a function of its volume
View SolutionThe electric current flowing in a circuit is given by i=((2t)/(3 tau)) A for some time.The rms value of current for the period t=0 to t=tau is
View Solution
Knowledge Check
A thermally insulated piece of metal is heated under atmosphere by an electric current so that it receives electric energy at a constant power P. This leads to an increase of the absoulute temperature T of the metal with time t as follows T=a14. then the heat capacity Cp is
A4PT3a4B4PT2)a3C4PT2DNone of theseA current carrying wire heats a metal rod. The wire provides a constant power P to the rod. The metal rod is enclosed in an insulated container. It is observed that the temperature (T) in the metal rod change with the (t) as T(t)=T0(1+βt1/4) where β is a constant with appropriate dimension of temperature. the heat capacity of metal is :
A4P(T(t)−T0)3β4T40B4P(T(t)−T0)2β4T30C4P(T(t)−T0)4β4T50D4P(T(t)−T0)β4T20If a piece of metal is heated to temperature θ and the allowed to cool in a room which is at temperature θ0, the graph between the temperature T of the metal and time t will be closet to
A B
B C
C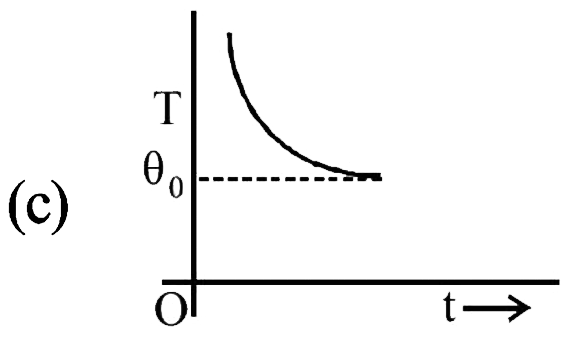 D
D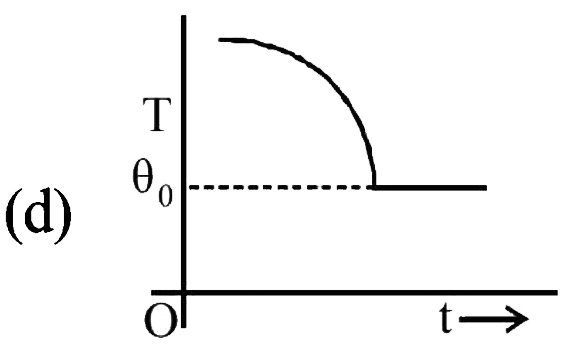
The current in a discharging LR circuit is given by I=i0e−tτ where τ is the time constant of the circuit. Calculate the rms current for the period t=0 to t=τ.
View SolutionThe electric current in a circuit is given by
i=3t
Here, t is in second and I in ampere. The rms current for the period to=0 to t=1 s is
View SolutionThe molar heat capacity for a gas at constant T and P is
View SolutionThe molar heat capacity for a gas at constant T and P is
View SolutionThe specific heat of a metal at low temperatures varies according to S=aT3, where a is a constant and T is absolute temperature. The heat energy needed to raise unit mass of the metal from temperature T=1K to T=2K is
View Solution