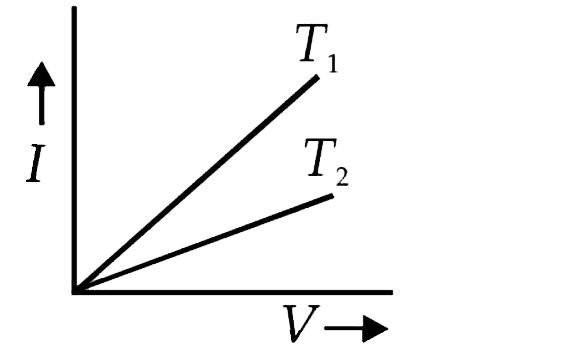
Figure. Shows the graphs of elongation versus temperature for two different metals. If these metals are employed to form a straight bimetallic strip of thickness 6 cm and heated, it bends in the form of an arc, the radius of cuvature chaging with temperature approximately as shown in the figure. The linear expansivities of the two metals are
24×10−6/∘C and 12×10−6/∘C
20×10−6/∘C and 10×10−6/∘C
18×10−6/∘C and 9xx10^(-6)//^@C
16×10−6/∘C and 8×10−6/∘C
The correct Answer is:D
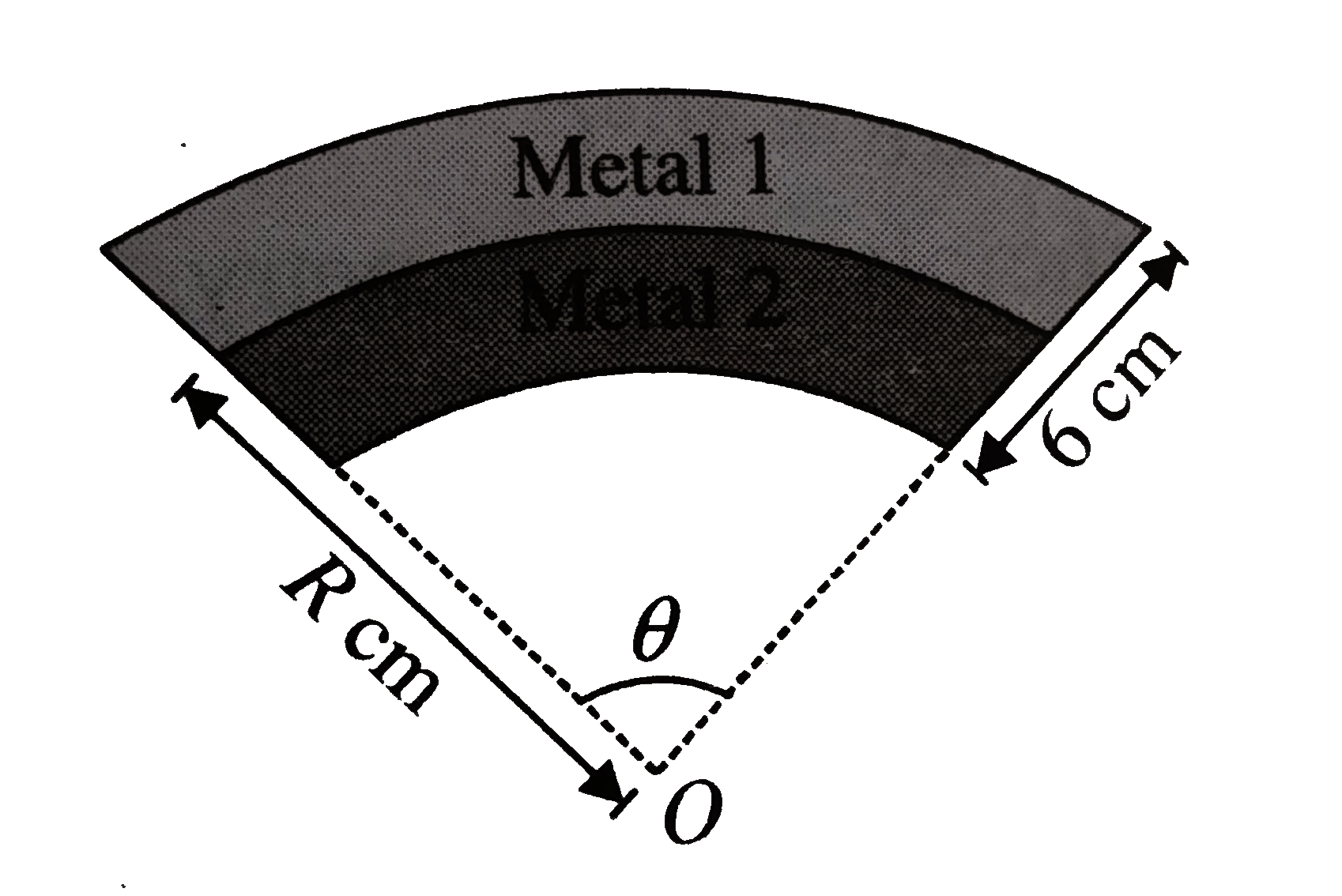
The slope of lines are
(ΔLΔT)1=Lα1=4−04−0=1 (For the first metal)
and (ΔLΔT)2=Lα2=2−04−0=12 (For the second metal)
and L0(1+α2T)=(R−1.5)θ
Dividing we get 1+α1T1+α2T=R+1.5R−1.5
or (α1−α2)T=3R and α1−α2=3RT from the graph shown in fig. (b)
α1−α2=37500×50=8×10−6/∘C
But α1α2=2
∴α1=16×10−6/∘C and a1=8×10−6/∘C
Topper's Solved these Questions
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Multiple Correct
25 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Comprehension
30 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Subjective
25 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICSCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
Knowledge Check
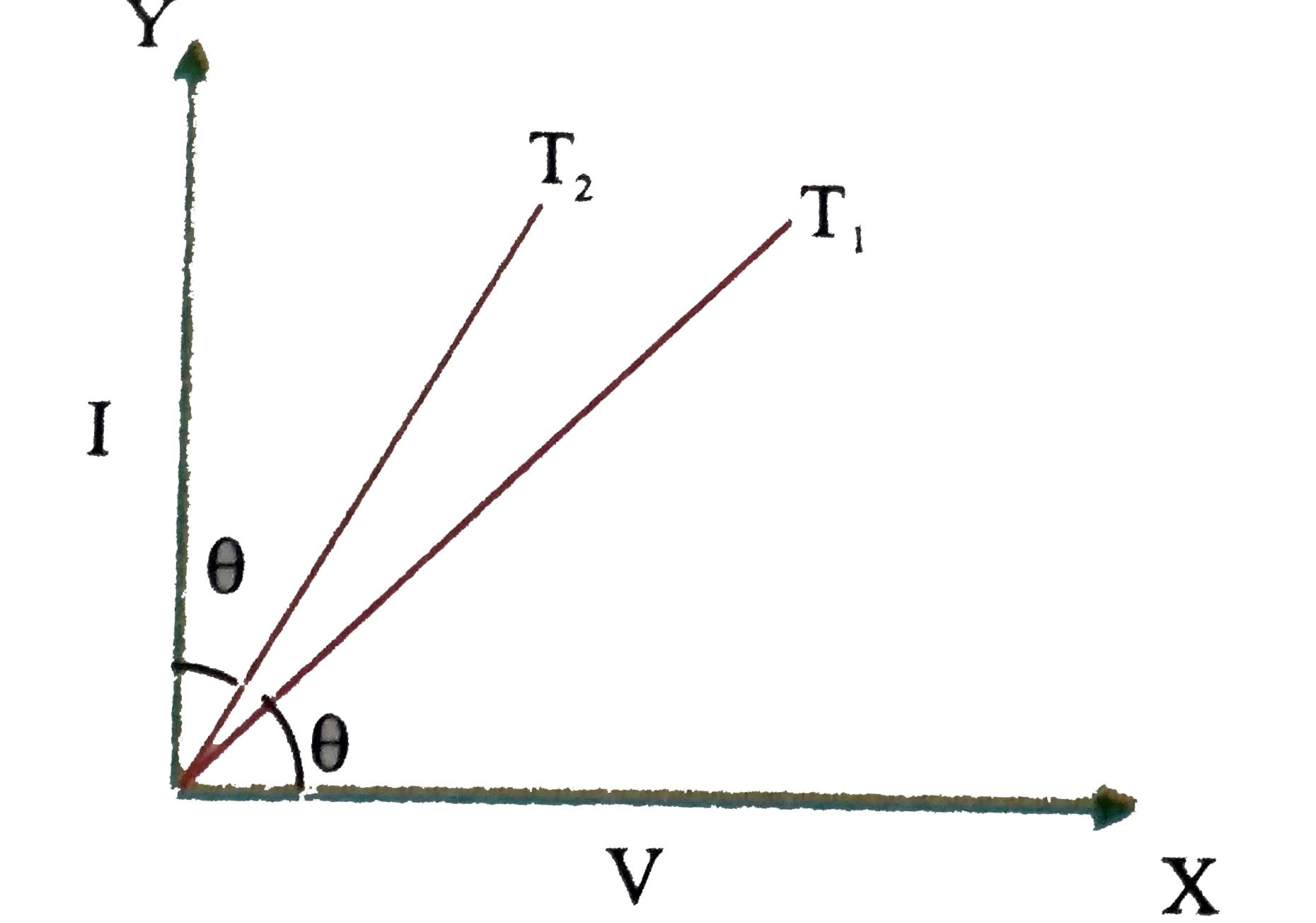
V−I graphs for a material is shown in the figure. The graphs are drawn at two different temperatures.AT1−T2∝cot2θBT1−T2∝sin2θCT1−T2∝tan2θDT1−T2∝cos2θThe wall of a house is made of two different materials of same thickness. The temperatures of the outer wall is T2 and that of inner wall is T1<T2. The temperature variation inside the wall as shown in the figure. Then :
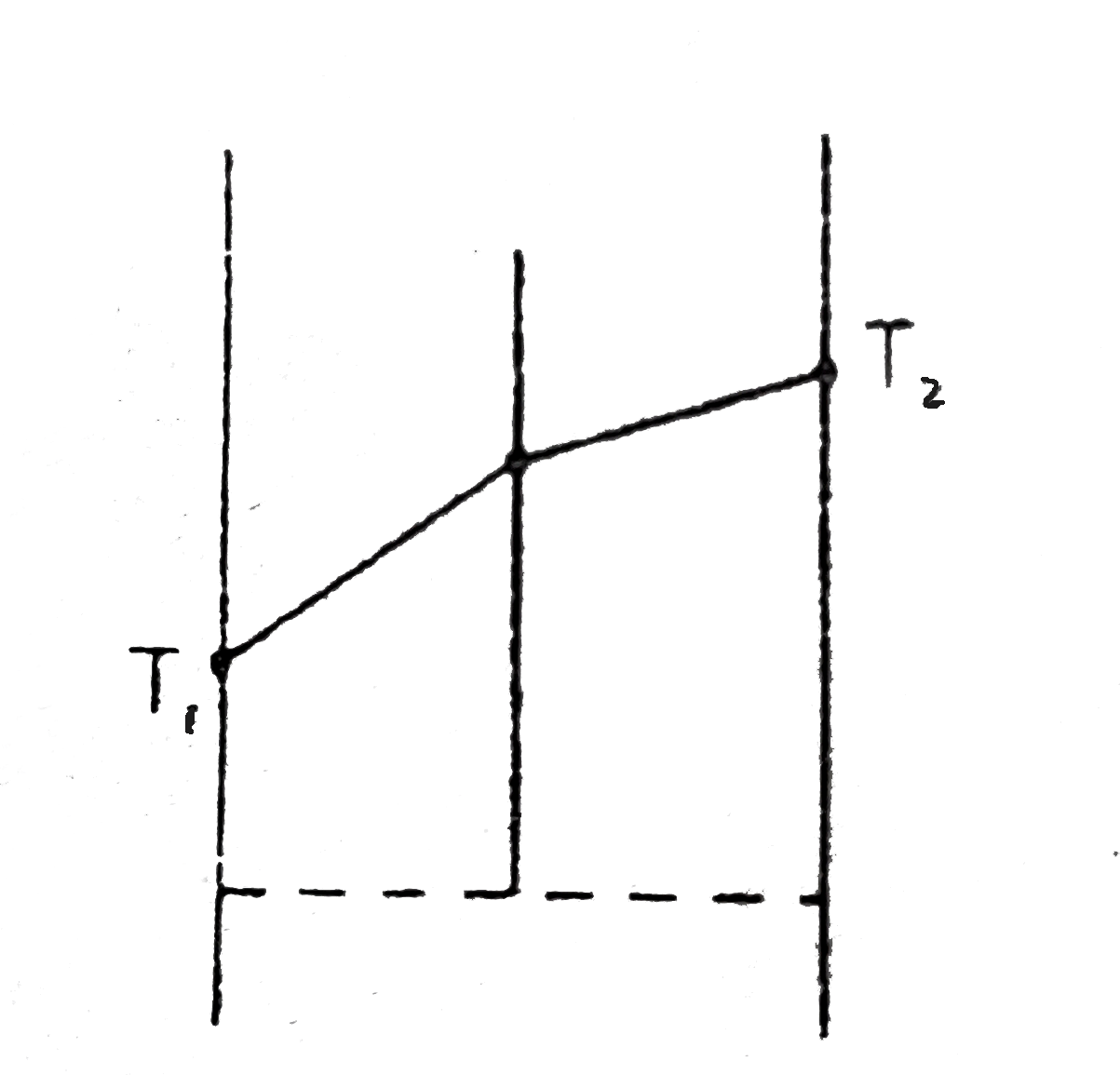Athermal conductivity of inner wall is greater than that of outerBthermal conductivity of outer wall is greater than that of innerCthermal conductivities of the two equalDno conclusion can be drawn about thermal conductivities
The variation of length of two metal rods A and B with change in temperature is shown in Fig. the coefficient of linear expansion αA for the metal A and the temperature T will beAαA=3×10−6/∘C,500∘CBαA=3×10−6/∘C,222.22∘CCαA=27×10−6/∘C,500∘CDαA=27×10−6/∘C,222.22∘C
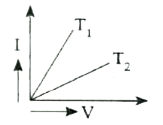
I-V graph for a metallie wire at two different tempearture, T1andT2 is as shown in the figure. Which of the two temperatures is lower and why ?
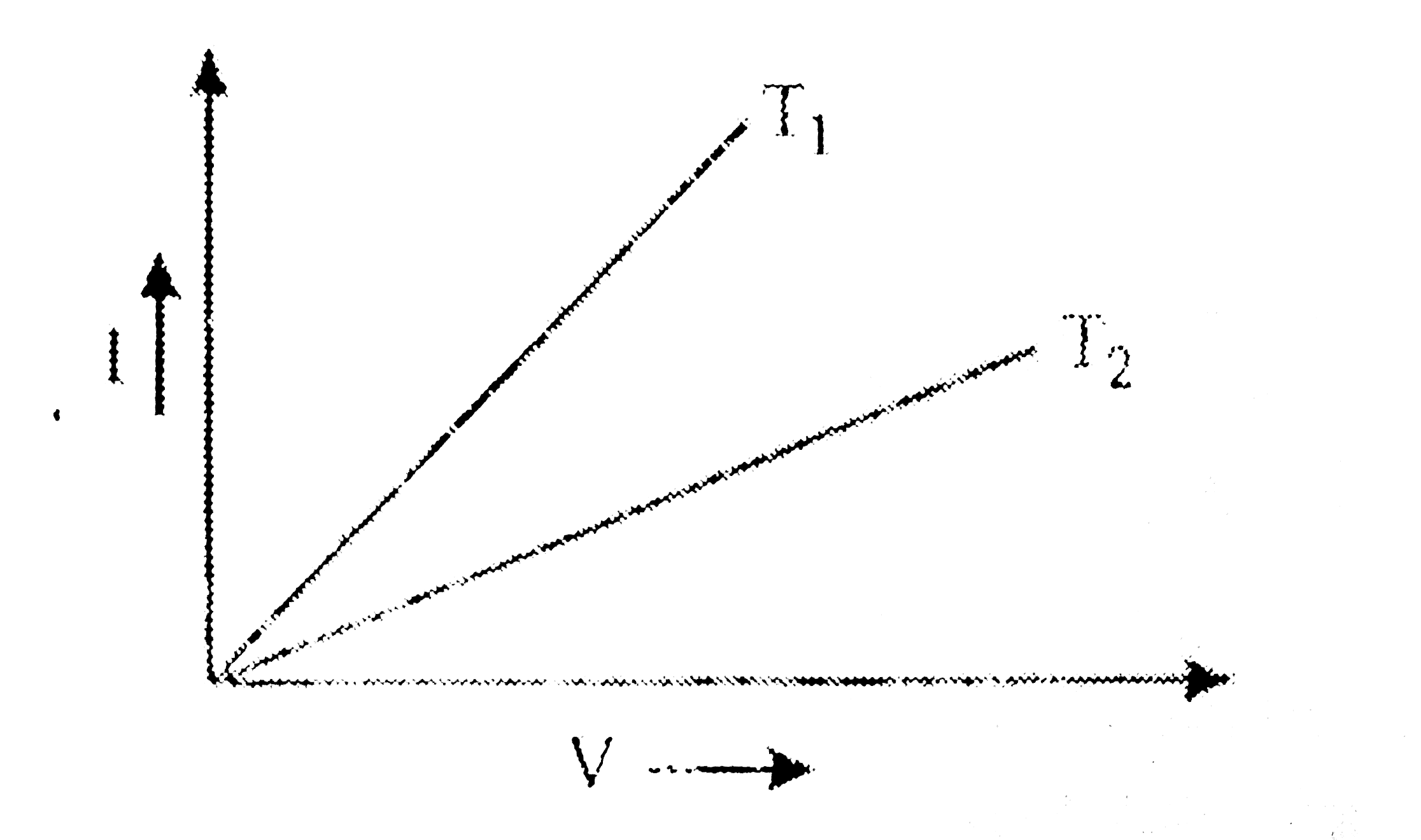
View SolutionThe current I and voltage V variations for a given metallic wire at tow different temperature T1andT2 are shown in the figure. Then which one of the following is correct
View Solutionfigures shows the expansion of a 2m long metal rod with temperature . The volume expansion coefficient the
metal is :-
_S01_079_Q01.png)
View SolutionBars of two different metals are bolted together , as shown in figure. The distance x does not change with temperature if :-
_E01_015_Q01.png)
View SolutionA bimetallic strip is formed out of two identical strips one of copper and the other of brass. The coefficients of linear expansion of the strip goes up by ΔTand the strip bends to from an arc of radius of curvature R. Then R is.
View Solution