The corfficient of linear expansion for a certain metal varies with temperature as . If is the initial elgnth of the metal and the temperature of metal is changed from to , then
The correct Answer is:B
As,
Topper's Solved these Questions
- CALORIMETRYBook:CENGAGE PHYSICSChapter:CALORIMETRYExercise:Multiple Correct
Explore 25 Videos
- CALORIMETRYBook:CENGAGE PHYSICSChapter:CALORIMETRYExercise:Comprehension
Explore 30 Videos
- CALORIMETRYBook:CENGAGE PHYSICSChapter:CALORIMETRYExercise:Subjective
Explore 25 Videos
- BASIC MATHEMATICSBook:CENGAGE PHYSICSChapter:BASIC MATHEMATICSExercise:Exercise 2.6
Explore 20 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
Coefficient of thermal expansion of a wire varies with temperature T as α=1.6×10−6T, where T is temperature in degree Celsius. If the length of wire is 10 m at0∘C, what is the change in length of wire (in mm), when its temperature is raised to 25∘C?
View SolutionI-V graph for a given metallic wire at two temperatures T1 and T2 is as shown in Fig. Which of the two temperatures is lower and why?
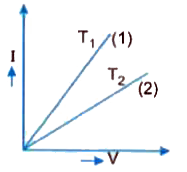
View Solution
Knowledge Check
The coefficient of linear expansion of a rod of length 1 m, at 27∘C, is varying with temperature as α = 2/T unit (300K≤T≤600K), where T is the temperature of rod in Kelvin. The increment in the length of rod if its temperature increases from 27∘C to 327∘C is
A0.3 mB3 mC0.4 mD4 m
The variation of length of two metal rods A and B with change in temperature is shown in Fig. the coefficient of linear expansion αA for the metal A and the temperature T will beAαA=3×10−6/∘C,500∘CBαA=3×10−6/∘C,222.22∘CCαA=27×10−6/∘C,500∘CDαA=27×10−6/∘C,222.22∘CEach side of a box made of metal sheet in cubic shape is 'a' at room temperature 'T', the coefficient of linear expansion of the metal sheet is 'α'. The metal sheet is heated uniformly, by a small temperature ΔT , so that its new temperature is T+ΔT . Calculate the increase in the volume of the metal box.
A3a3αΔTB4a2αΔTC4πa∧3αΔTD43πa3αΔT
The coefficient of linear expansion 'α' of the material of a rod of length l0 varies with absolute temperature as α=aT−bT2 where a & b are constant. The linear expansion of the rod when heated from T1 to T2=2T1 is :-
View SolutionA rod of length l and coefficient of linear expansion α. Find increase in length when temperature changes from T to T+ ΔT
View SolutionA rod of length l and coefficient of linear expansion α. Find increase in length when temperature changes from T to T+ ΔT
View SolutionThe radious of a metal sphere at room temperature T is R, and the coefficient of linar expansion of the metal is α. The sphere is heated a little by a temperature ΔT so that its new temperature is T+ΔT. The increase in the volume of the sphere is approximately
View SolutionPressure P, volume V and temperature T of a certain material are related by P=αT2/V where α is contant. Work done by the material when temperature changes from T0 to 2T0 and pressure remains constant is
View Solution