
Three rods AB, BC and BD of same length l and cross section A are arranged as shown. The end D is immersed in ice whose mass is 440 g and is at 0∘C. The end C is maintained at 100∘C. Heat is supplied at constant rate of 200 cal/s. Thermal conductivities of AB, BC and BD are K, 2K and K/2, respectively Time after which whole ice will melt is (K=100cal/m−s∘CA=10cm2,l=1cm)
400 s
600 s
700 s
800 s
The correct Answer is:D
Let θ be the temperate of B
2KA(θ−100)l+(K2)A(θ−0)l=200
Substituting values θ=880∘C
Also from B→D,K2A(θ−0)l=4405×80
t=800s
Related Playlists
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Multiple Correct25videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Comprehension30videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Subjective25videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.620videos
BASIC MATHEMATICS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE1videos
CENTRE OF MASS
Similar Questions
Three rods AB,BC and BD of same length l and cross-sectionsl area A are arranged as shown . The end D is immersed in ice whose mass is 440gm Heat is being supplied at constant rate of 200cal/sec from the end Time in which whole ice will melt (Latent heat of fusion of ice is 80cal/gm
 .View Solution
.View SolutionThree rods AB,BC and BD of same length l and cross-sectional area A are arranged, The end D is immersed in ice whose mass is 440g. Heat is being supplied at constant rate of 200cals from the end A. The time (in s) in which whole ice will melt is (Given:k (thermal condactivity) =100 cal m−1s−1o C−1,A= 10 cm^2, l=1 m, latent heat of fusion of ice is 80 cal g.)
'(##CEN_KSR_PHY_JEE_C13_E01_039_Q13##)'View SolutionThree rods A, B and C of the same length and same cross-sectional area are joined as shown. Their thermal conductivities are in the ratio 1:2:3/2. If the open ends of A and C are at 200∘C and 18∘C, respectively, then the temperature at the junction of A at steady state is
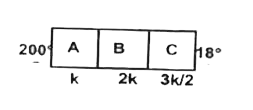 View Solution
View SolutionThree metal rod A, B and C of same length and cross-section are placed end to end and a temperature difference is maintained between the free ends of A and C. If the thermal conductivity of B(KB) is twice that of C(KC) and half that of A(KA), then the effective thermal conductivity of the system will be
View SolutionOne end of 0.5 m long metal rod is in steam at 100∘C and the other end is put in ice at 0∘C. If ice melts at the rate of 10 g/min, calculate the thermal conductivity of the metal. Take, cross sectional area of rod=2πcm2 . Latent ice of heat = 80 cal/g
View SolutionThree rods AB,BC and BD made of the same materical and having the same area of cross section have been joined as shown is the The ends A,C and D are held at temperatures 20∘C Cand 80∘C respectively If each rod is of same length then find the temperature at the junction B of the three rods
 .View Solution
.View SolutionThree rods each of same length and cross - section are joined in series. The thermal conductivity of the materials are K, 2K and 3K respectively. If one end is kept at 200∘C and the other at 100∘C. What would be the temperature of the junctions in the steady state? Assume that no heat is lost due to radiation from the sides of the rods.
View SolutionThree conducting rods of same material and cross-section are shown in figure. Temperatures of A,D and C are maintained at 20∘C,90∘Cand0∘C. The ratio of lengths BD and BC if there is no heat flow in AB is
 View Solution
View SolutionThree rods of the same dimension have thermal conductivities 3K, 2K and K. They are arranged as shown in fig. Given below, with their ends at 100∘C,50∘C and 20∘C. The temperature of their junction is :-
 View Solution
View SolutionTwo rods of similar area of cross section and length are joined as shown in the figure. The ratio of their thermal conductivity is 2:3. The free ends are maintained at 100∘C and 0∘C respectivley. THE temperature at junction in steady state is
 View Solution
View Solution


