Three rods each of same length and cross - section are joined in series. The thermal conductivity of the materials are K, 2K and 3K respectively. If one end is kept at 200∘C and the other at 100∘C. What would be the temperature of the junctions in the steady state? Assume that no heat is lost due to radiation from the sides of the rods.
The correct Answer is:A, B, C, D
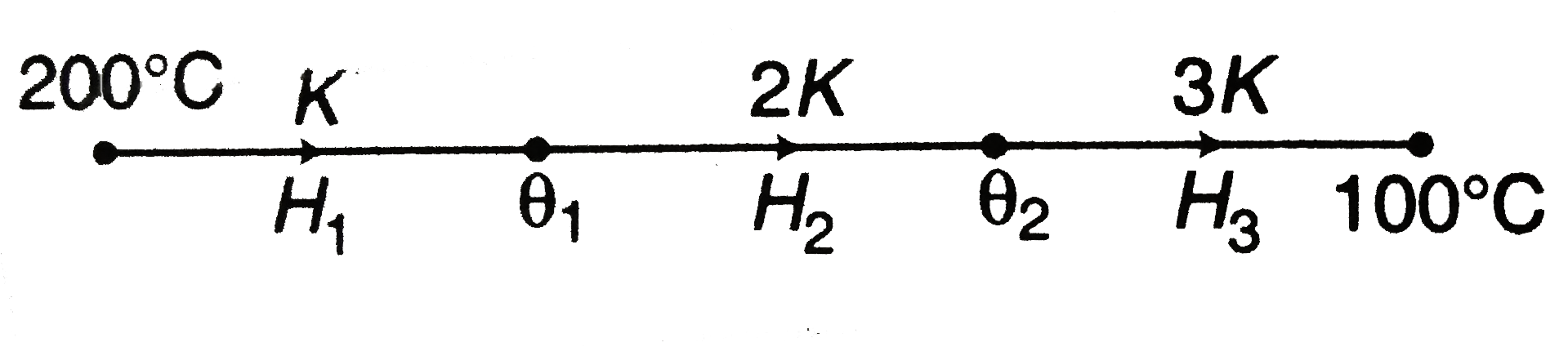
H1=H2=H3
∴200−θ1(1/KA)=θ1−θ2(l/2KA)=θ2−100(l/3KA)
Solving these equations we get,
θ1=145.5∘C
and θ2=118.2∘C .
Topper's Solved these Questions
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Assertion And Reason
10 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 1 Objective
11 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Exercise 22.1
7 Videos
- BASIC MATHEMATICSBOOK - DC PANDEYCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise
13 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
Similar Questions
Three rods made of same material and having the same cross-section have been joined as shown in fig. each rod is of the same length. The left and the right ends are kept at 0∘C and 90∘C respectively. What will be the temperature of the junction of the three rods?

View Solution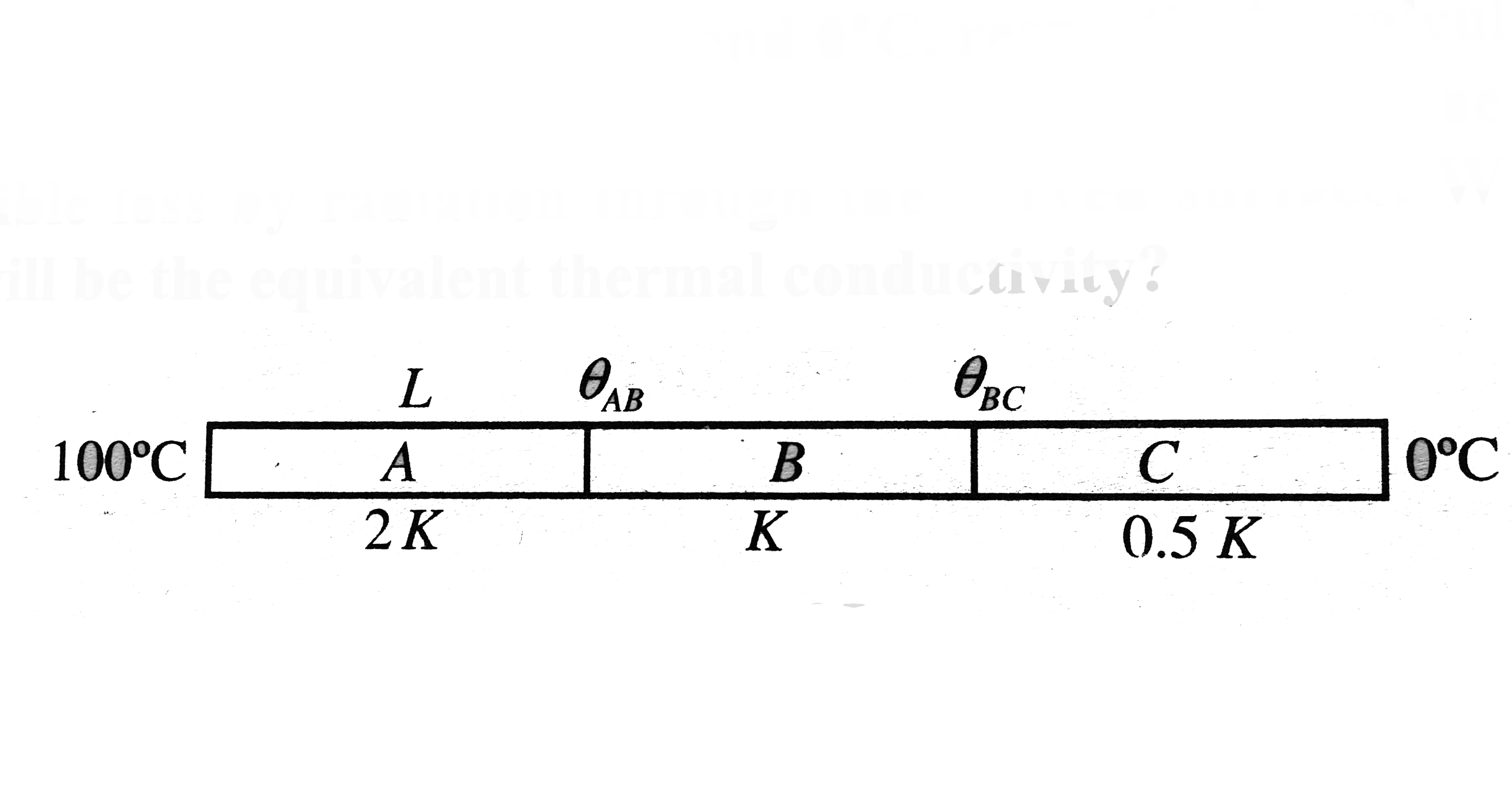
Three cylindrical rods A, B and C of equal lengths and equal diameters are joined in series as shown if Fig. Their thermal conductivities are 2K, K and 0.5K, respectively. In steady state, if the free ends of rods A and C are at 100∘C and 0∘C, respectively, calculate the temperature at the two junction points. Assume negligible loss by radiaiotn through the curved surface. What will be the equivalent thermal conductivity?
View Solution
Knowledge Check
Three rods A, B and C of the same length and same cross-sectional area are joined as shown. Their thermal conductivities are in the ratio 1:2:3/2. If the open ends of A and C are at 200∘C and 18∘C, respectively, then the temperature at the junction of A at steady state is
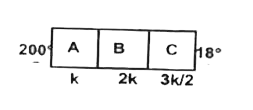 A156∘CB148∘CC116∘CD74∘C
A156∘CB148∘CC116∘CD74∘CThree rods A,B and C of the same length and cross- sectional area are joined in series as shown. The temperature at the junction of A and B, in equilibriu, is
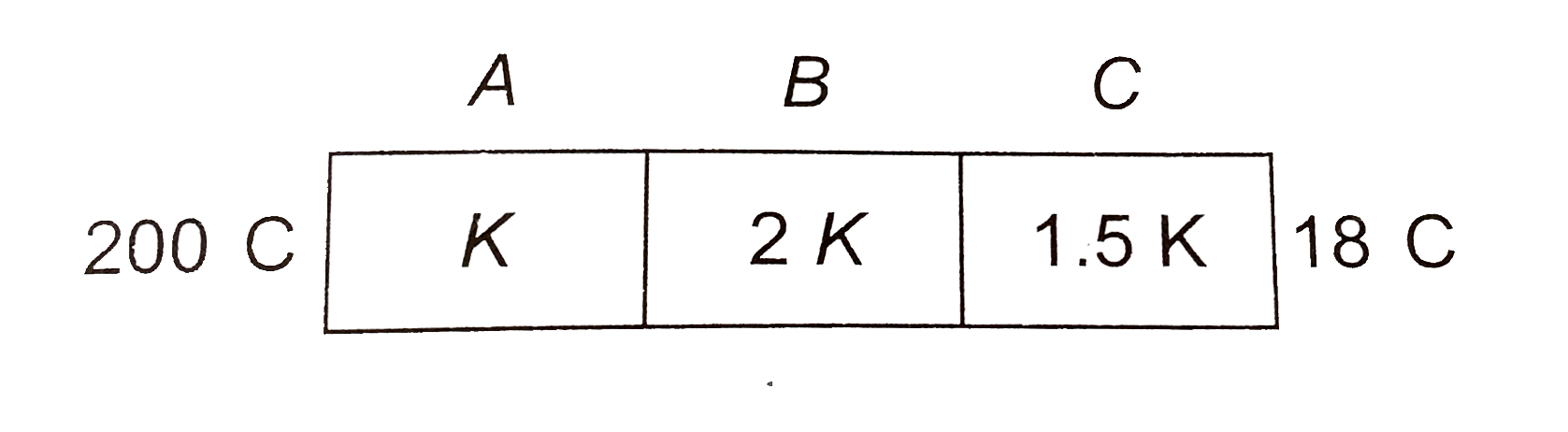 A74∘CB116∘CC156∘CD148∘C
A74∘CB116∘CC156∘CD148∘CA composite rod made of three rods of equal length and cross-section as shown in fig. The thermal conductivites of the materials of the rods are K/2, 5K and K respectively. The end A and end B are at constant tempertures. All heat entering the face A goes out of the end B there being no loss of heat from the sides of the bar. The effective thermal conductivity of the bar is
 A15K/16B6K/13C5K/16D2K/3
A15K/16B6K/13C5K/16D2K/3
Three identical rods are joined in series as shown. Their thermal conductivities are K,K/2 and K/3 respectively. At steady, if the free ends of rods are at 100∘C and 20∘C respectively. Determine the temperature at two junction points. Also find the equivalent thermal conductivity.
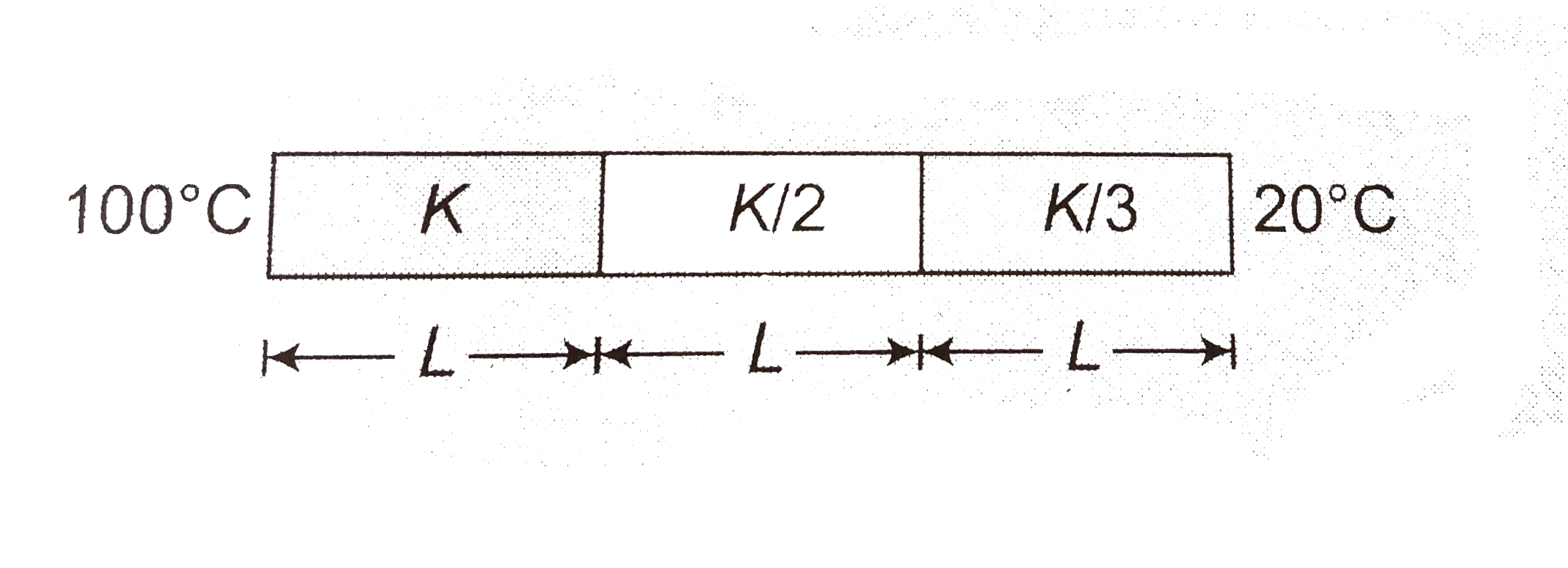
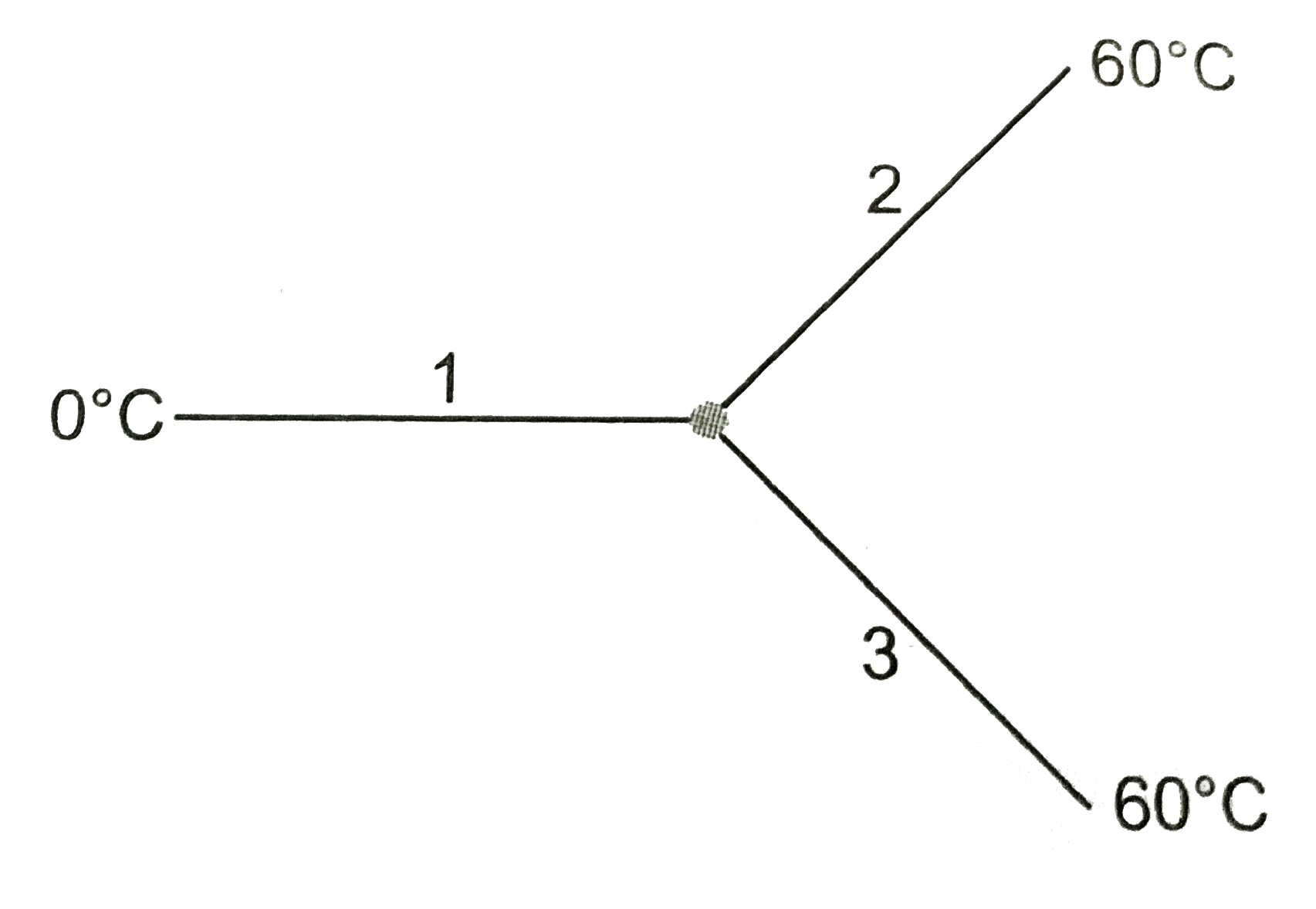
View SolutionThree rods made of same material and having same cross-section have been joined as shown in Fig. 7(e).18. Each rod is of the same length. The left and the right ends are kept at 0∘C and 60∘C respectively. What is the temperature of the junction of the three rods.
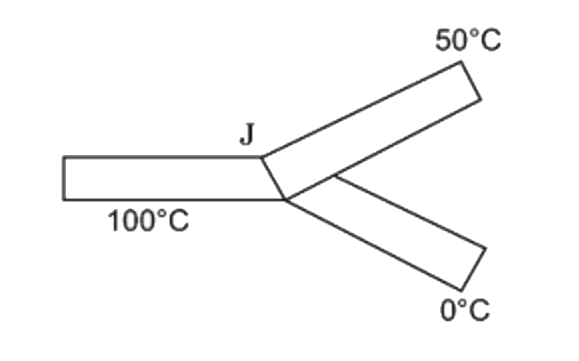
View SolutionThree rods of same dimensions have thermal conductivities 3K, 2k and K, with their ends at 100∘C,50∘Cand0∘C respectively . They re arranged as shown in the diagram . The temperature of the junction J in steady -state is
View SolutionThree rods of same dimension are joined in series having thermal conductivity k1 , k2 and k3. The equivalent thermal conductivity is
View SolutionThree rods made of same material and having the same cross-section have been joined as shown. In the figure.Each rod is of the same length. The left and right ends are kept at 0∘Cand90∘C respectively. The temperature of the junction of the three rods will be
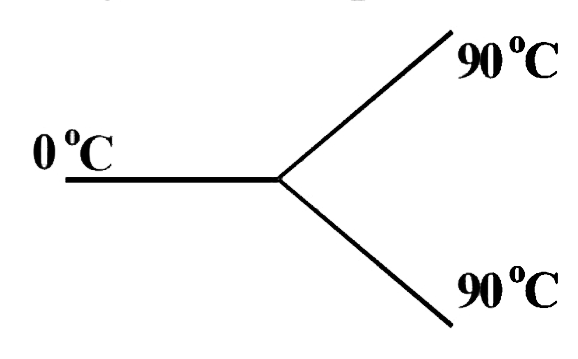
View Solution
