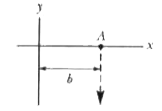
A particle of mass is released in vertical plane from a point at on the -axis. It falls vertically parallel to the -axis. Find the torque acting on the particle at a time about origin.

Torque is produced by the force of gravity.
or
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Solved Examples
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.1
6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
A particle of mass m is released from rest from point P at x=x0 on X-axis from origin O and falls vertically along y-axis as shown in Fig. What is the magnitude of the torque acting on the particle at time t, when it is at the point Qw.r.t.O ?
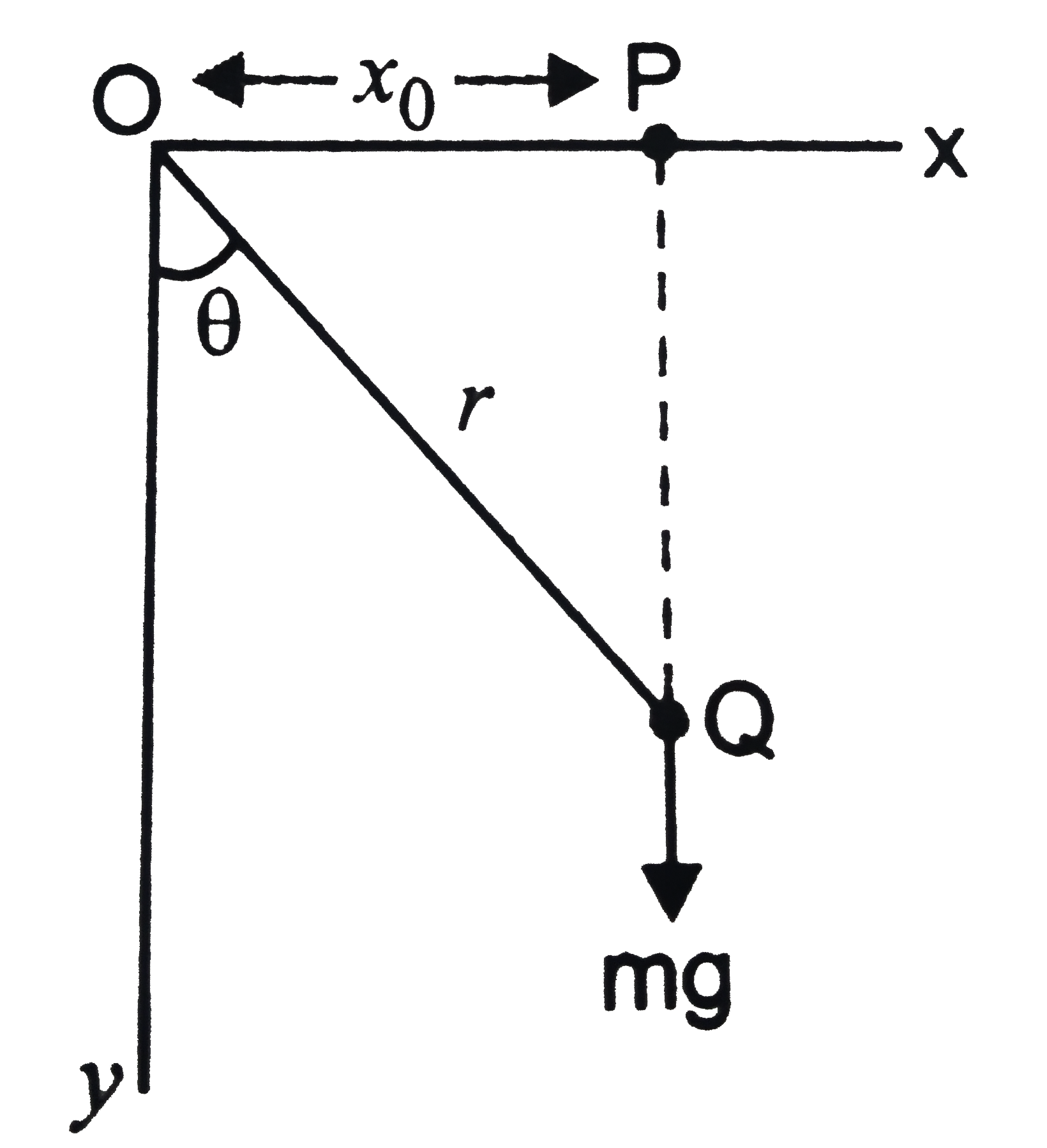
View SolutionA particle of mass m is released from rest at point A in Fig., falling parallel to the (vertical) y-axis. Find the angular momentum of the particle at any time t with respect to the same origin O.
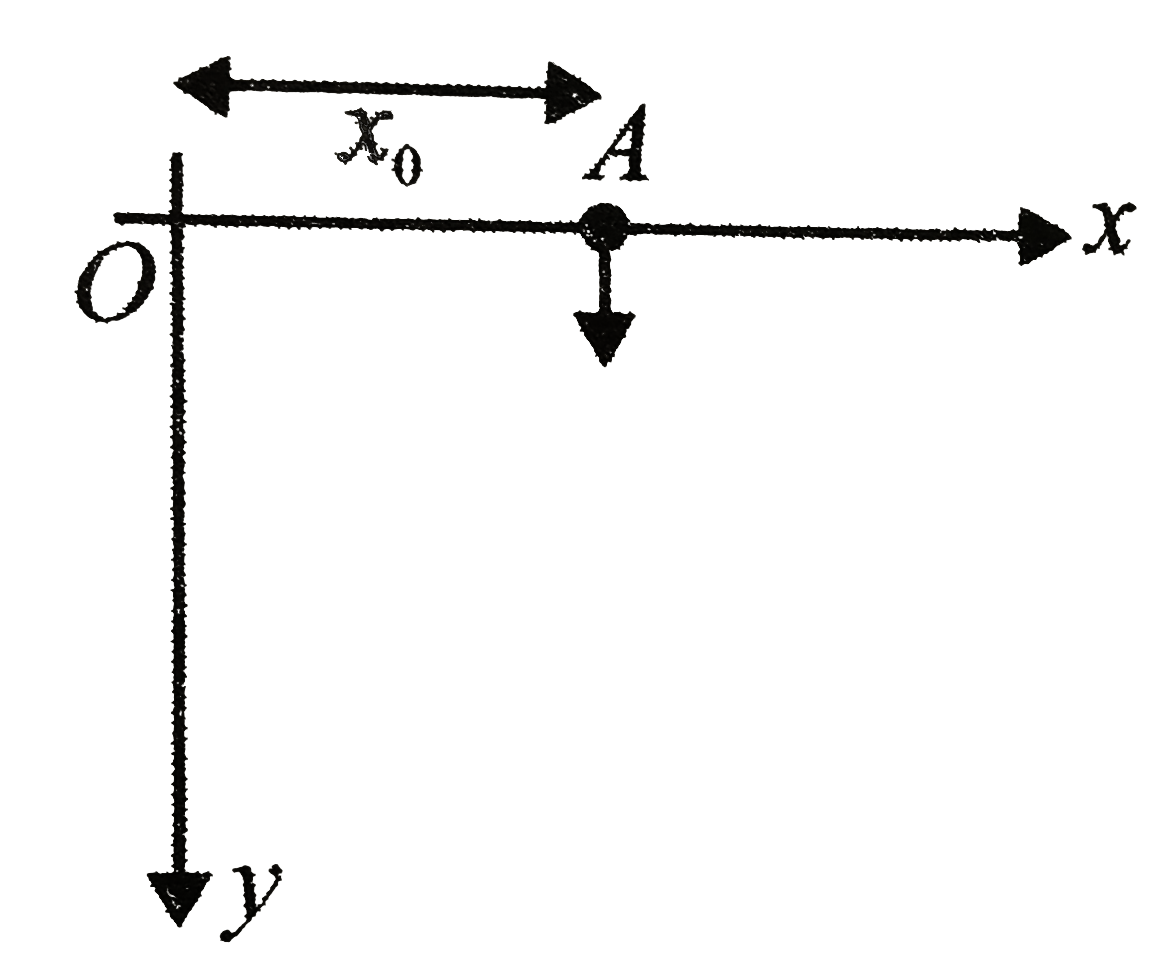
View Solution
Knowledge Check
A particle is moving parallel to x-axis as shown in the figure. The angular velocity of the particle about the origin is
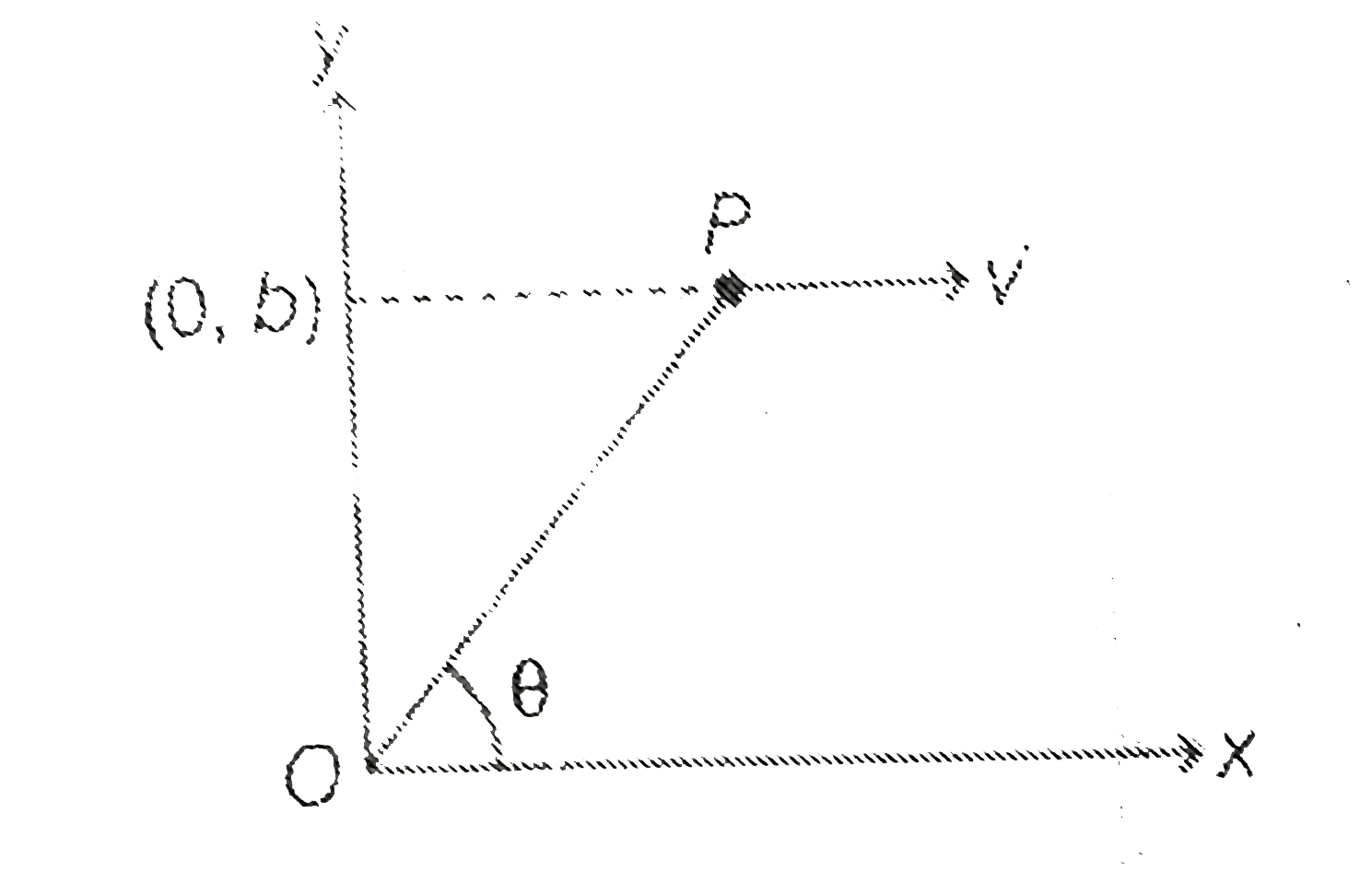 A(v/b)sin2θB(v/b)C(v/b)sinθDvbsinθ
A(v/b)sin2θB(v/b)C(v/b)sinθDvbsinθA particle of mass m is released from rest at point A in the figure falling freely under gravity parallel to the vertical Y-axis. The magnitude of angular momentum of particle about point O when it reaches B is (where OA=b and AB=h)
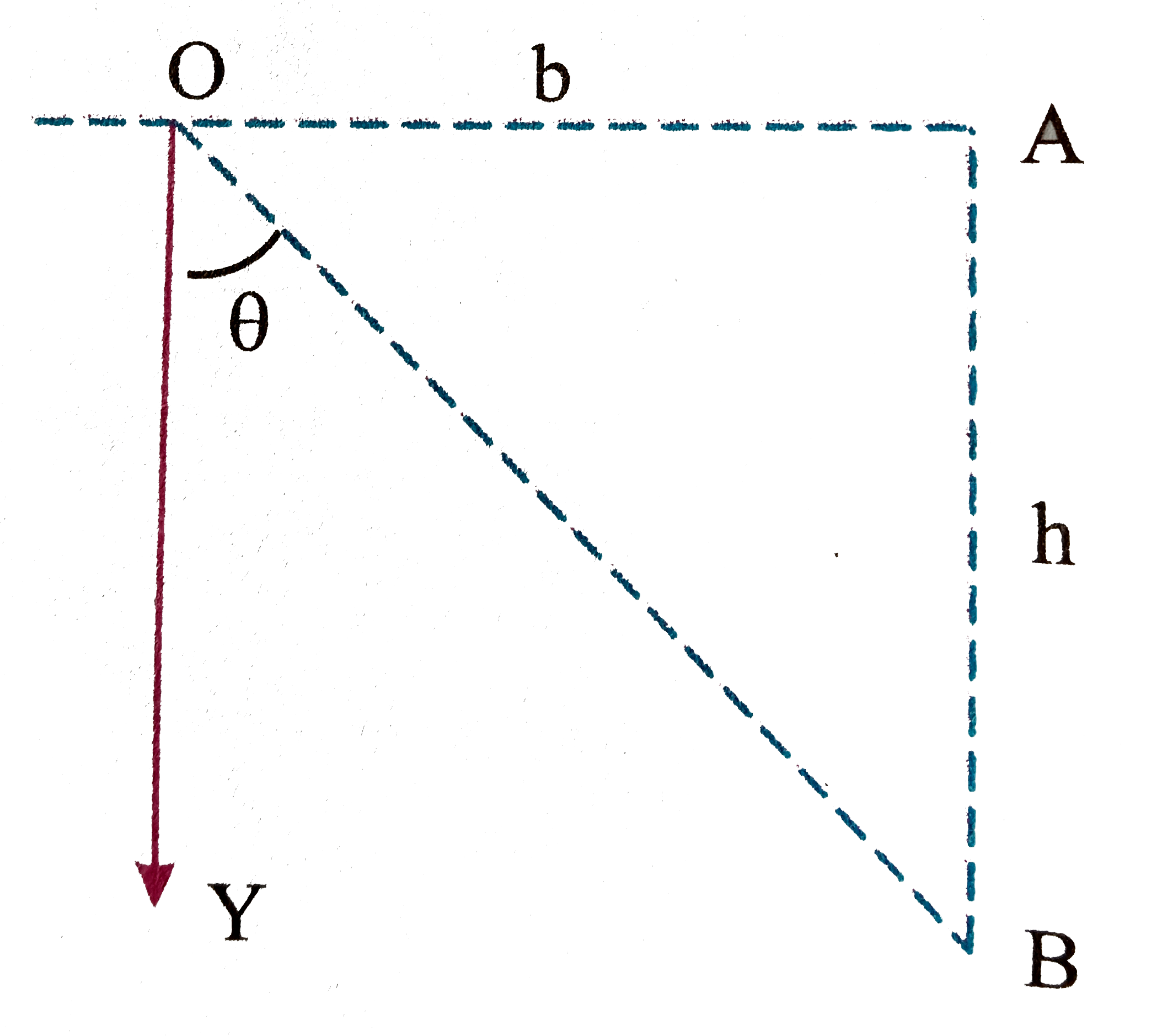 AmhbgBmgb√2ghCmb√3ghD2mb√gh
AmhbgBmgb√2ghCmb√3ghD2mb√ghTwo charges, each equal to q, are kept at x=−a and x=a on the x-axis. A particle of mass m and charge q0=q2 is placed at the origin. If charge q0 is given a small displacement (y<<a) along the y-axis, the net force acting on the particle is proportional to
A(a) yB(b) −yC(c) 1yD(d) −1y
A particle of mass m is projected from origin O with speed u at an angle θ with positive x-axis. Positive y-axis is in vertically upward. Direction. Find the angular momentum of particle at any time t about O before the particle strkes the ground again.
View SolutionIn Fig. 10-73, a particle of mass m is released from rest at point A, at distance b from the origin, and falls parallel to a vertical y axis. As a function of time t and with respect to the origin, find the magnitudes of (a) the torque τ on the particle due to the gravitational force and (b) the angular momentum L of the particle. ( c) From those results, verify that τ=dL/dt.
View SolutionA particle of mass m is moving with constant speed in a vertical circle in X−Z plane. There is a small both at some distance on Z−axis. The maximum distance of the shadow of the particle on X−axis from origin equal to :−
View Solution
A particle is projected from the horizontal x-z plane, in vertical x-y plane where x-axis is horizontal and positive y-axis vertically upwards. The graph of y coordinate of the particle v/s time is as shown . The range of the particle is √3. Then the speed of the projected particle is:
View SolutionA particle is moving in the xy-plane with a constant velocity along a line parallel to the X-axis away from the origin. The magnitude of its angular momentum about the origin.
View Solution
