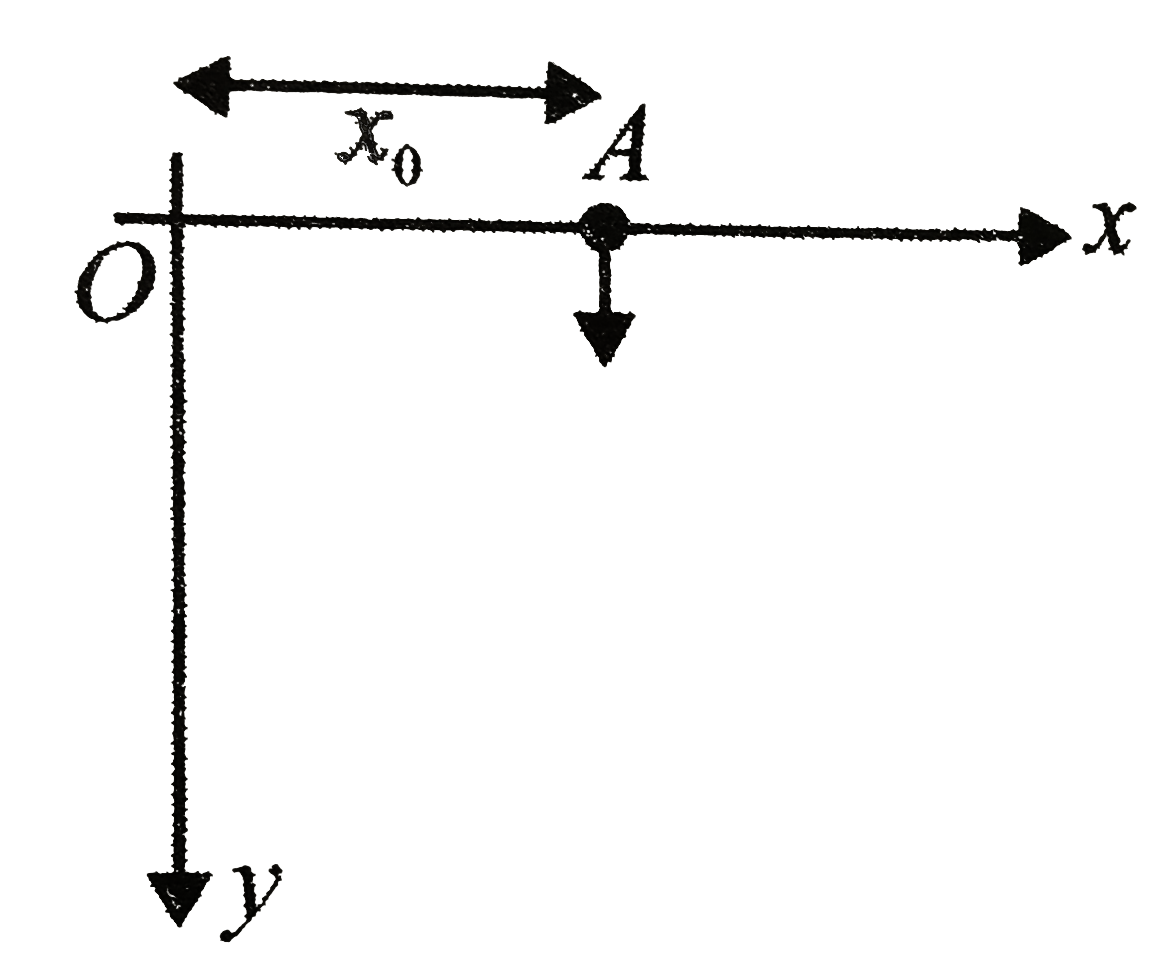
A particle of mass m is released from rest from point P at x=x0 on X-axis from origin O and falls vertically along y-axis as shown in Fig. What is the magnitude of the torque acting on the particle at time t, when it is at the point Qw.r.t.O ?
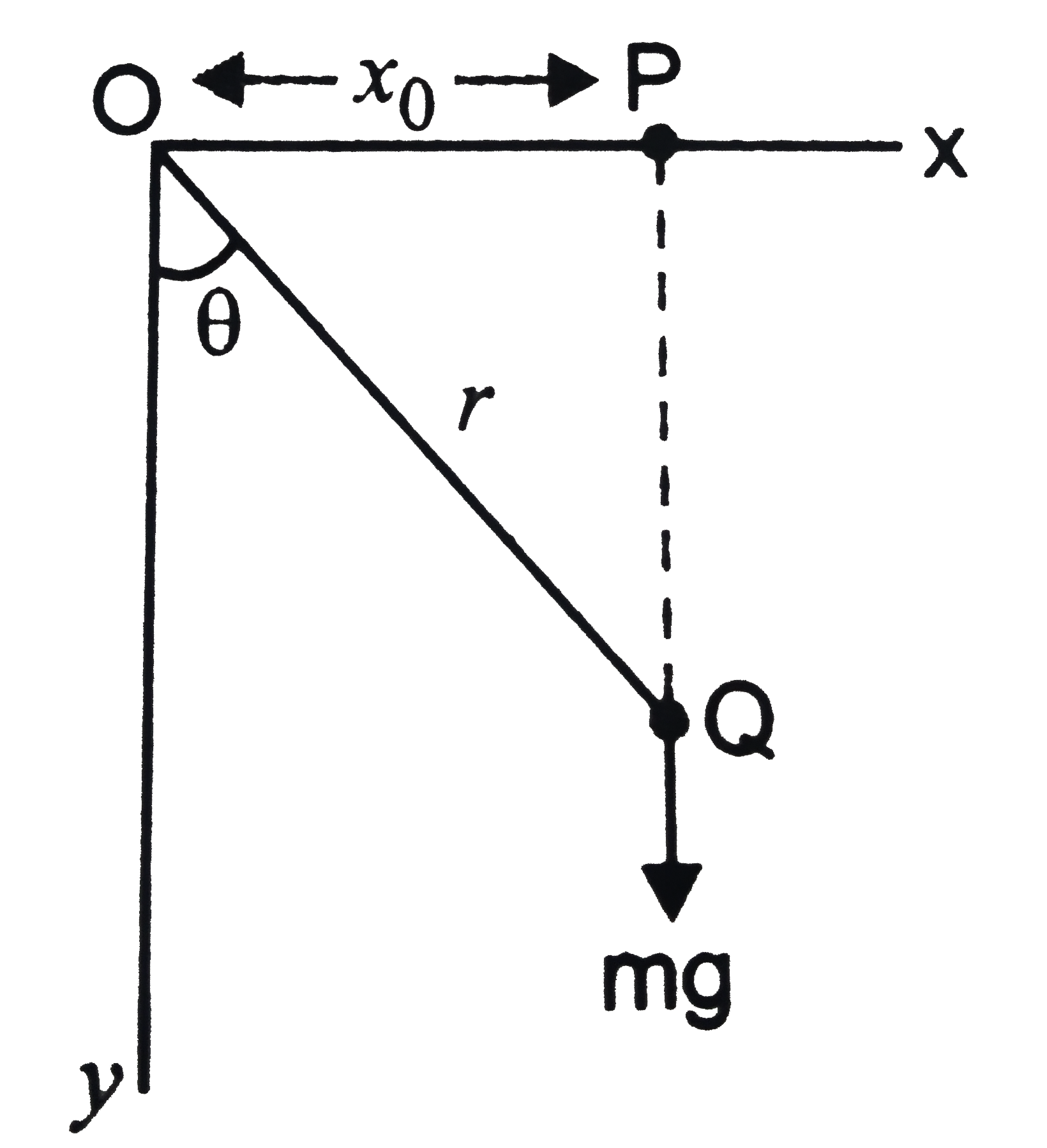
Refer to Fig.
Magnitude of torque is
τ=rFsinθ=r×mg×x0r=mgx0

Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:PROBLEMS FOR PRACTICE TYPE B
Explore 2 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:PROBLEMS FOR PRACTICE TYPE C
Explore 2 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:PROBLEMS FOR PRACTICE TYPE A
Explore 2 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:Assertion- Reason Type Questions
Explore 19 Videos
Similar Questions
A particle of mass m is released in vertical plane from a point P at x=x0 on the x-axis. It falls vertically parallel to the y-axis. Find the torque τ acting on the particle at a time about origin.

View SolutionIn Fig. 10-73, a particle of mass m is released from rest at point A, at distance b from the origin, and falls parallel to a vertical y axis. As a function of time t and with respect to the origin, find the magnitudes of (a) the torque τ on the particle due to the gravitational force and (b) the angular momentum L of the particle. ( c) From those results, verify that τ=dL/dt.
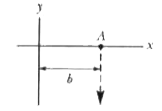
View Solution
Knowledge Check
A particle of mass m is released from rest at point A in the figure falling freely under gravity parallel to the vertical Y-axis. The magnitude of angular momentum of particle about point O when it reaches B is (where OA=b and AB=h)
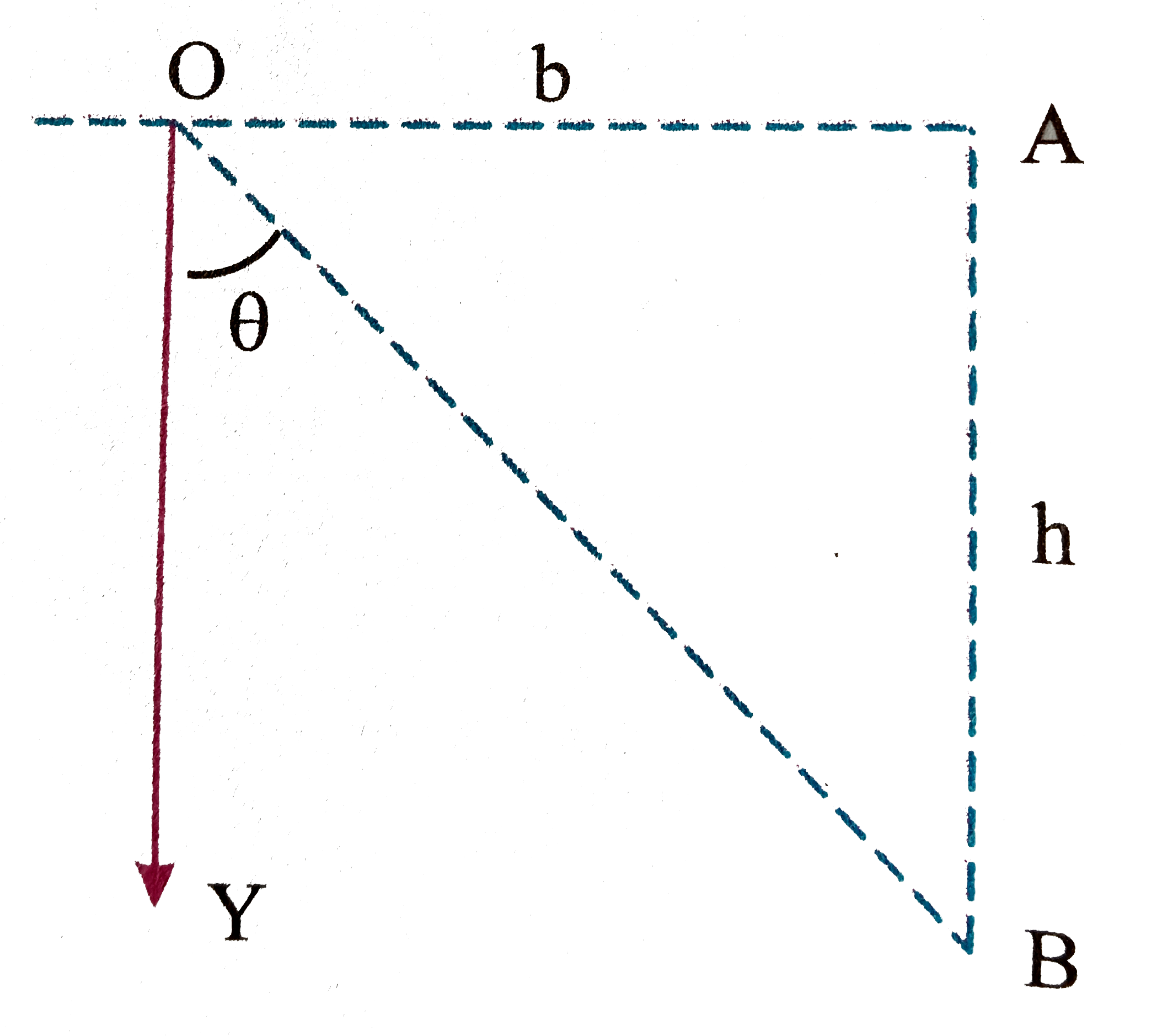 AmhbgBmgb√2ghCmb√3ghD2mb√gh
AmhbgBmgb√2ghCmb√3ghD2mb√ghvx is the velocity of a particle moving along the x-axis as shown in the figure. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s ?
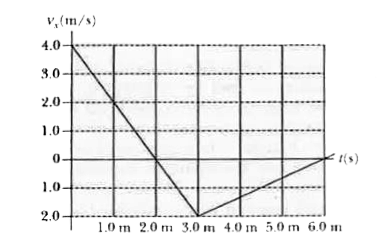 A−2.0 mB+2.0 mC+1.0 mD−1.0 m
A−2.0 mB+2.0 mC+1.0 mD−1.0 mVx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?
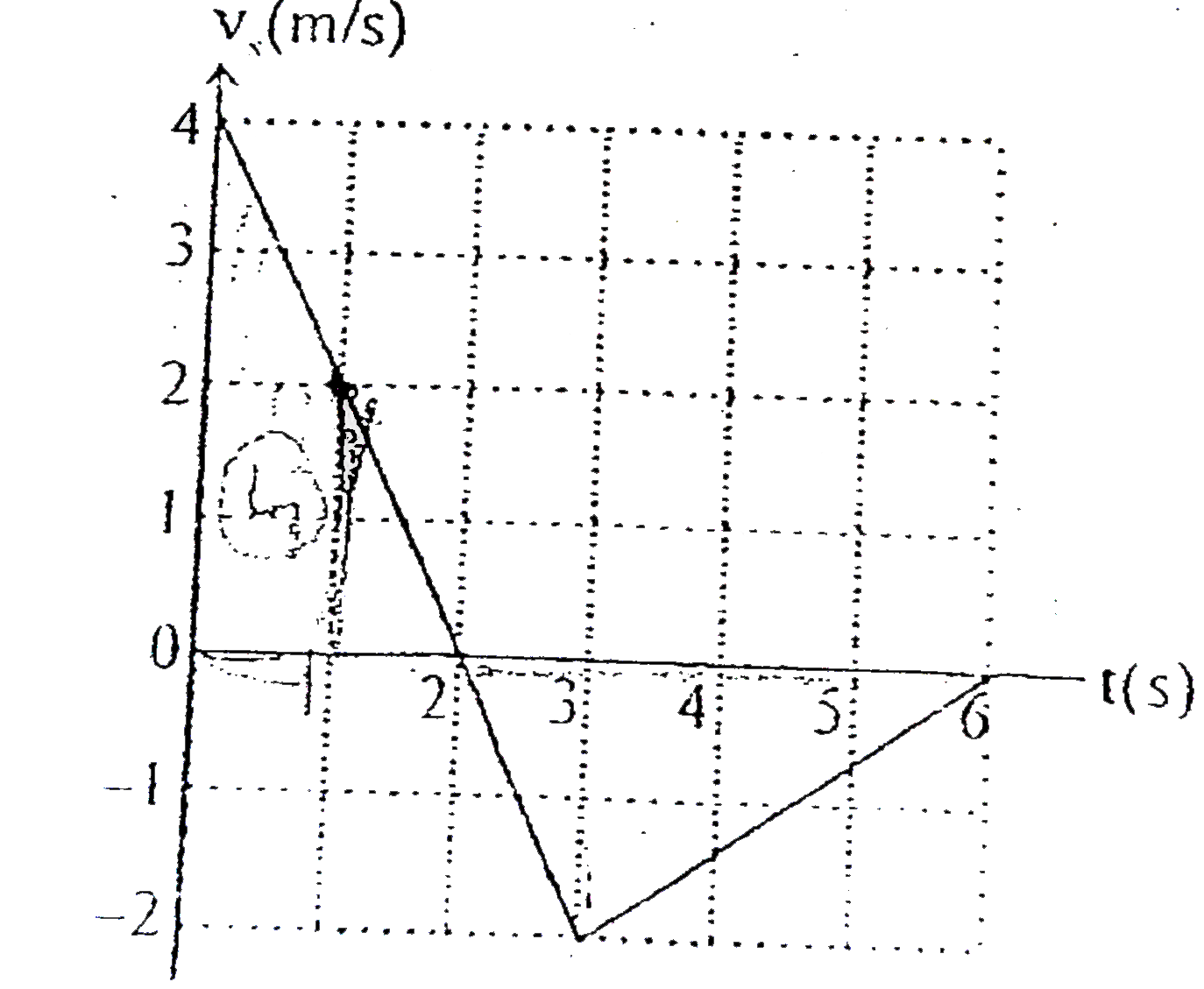 A−2.0mB+2.0mC+1.0mD−1.0m
A−2.0mB+2.0mC+1.0mD−1.0m
A particle of mass m is released from rest at point A in Fig., falling parallel to the (vertical) y-axis. Find the angular momentum of the particle at any time t with respect to the same origin O.
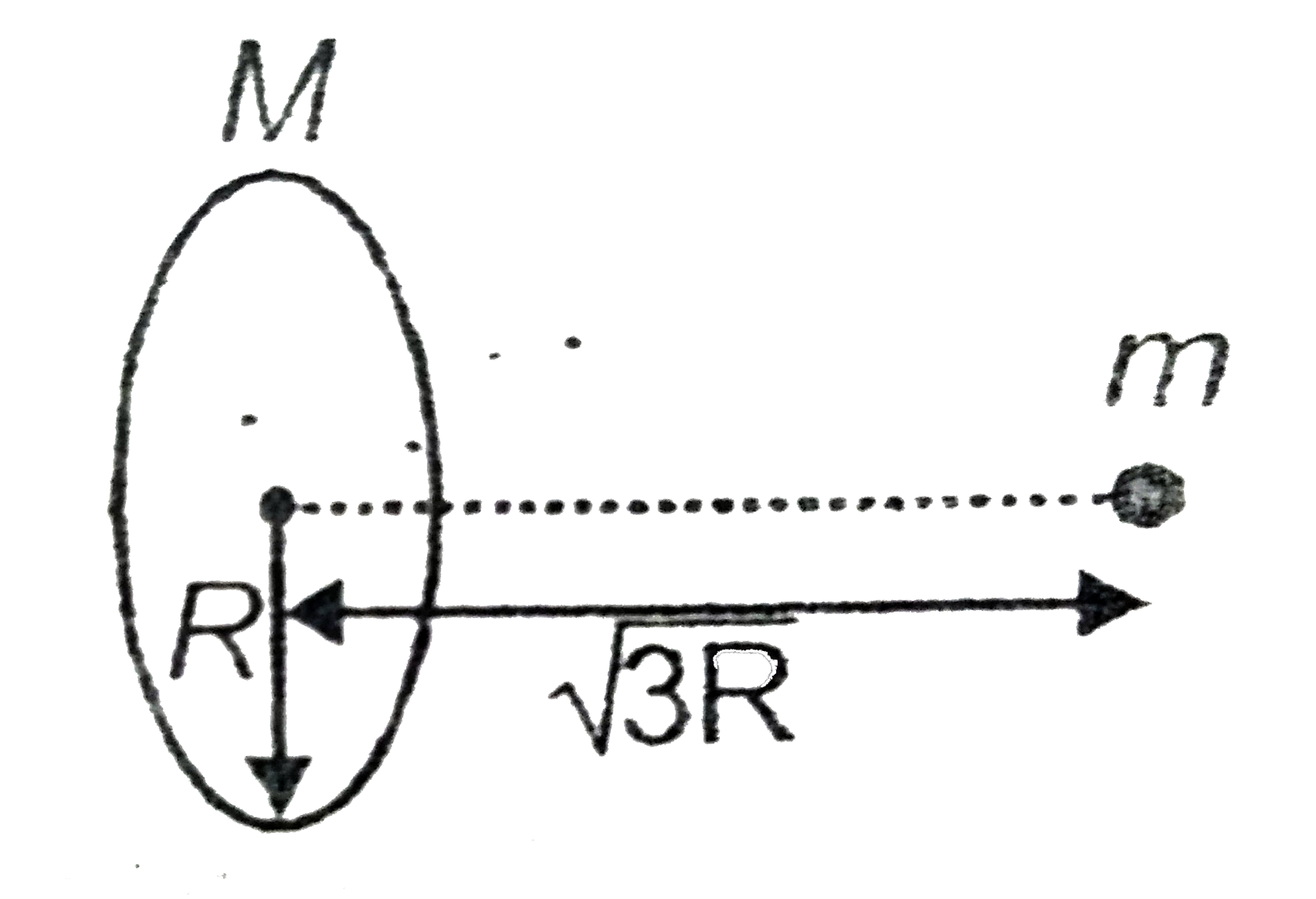
View SolutionA point particle of mass m is released from a distance √3R along the axis of a fixed ring of mass M and radius R as shown in figure. Find the speed of particle as it passes through the centre of the ring.
View SolutionA particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?
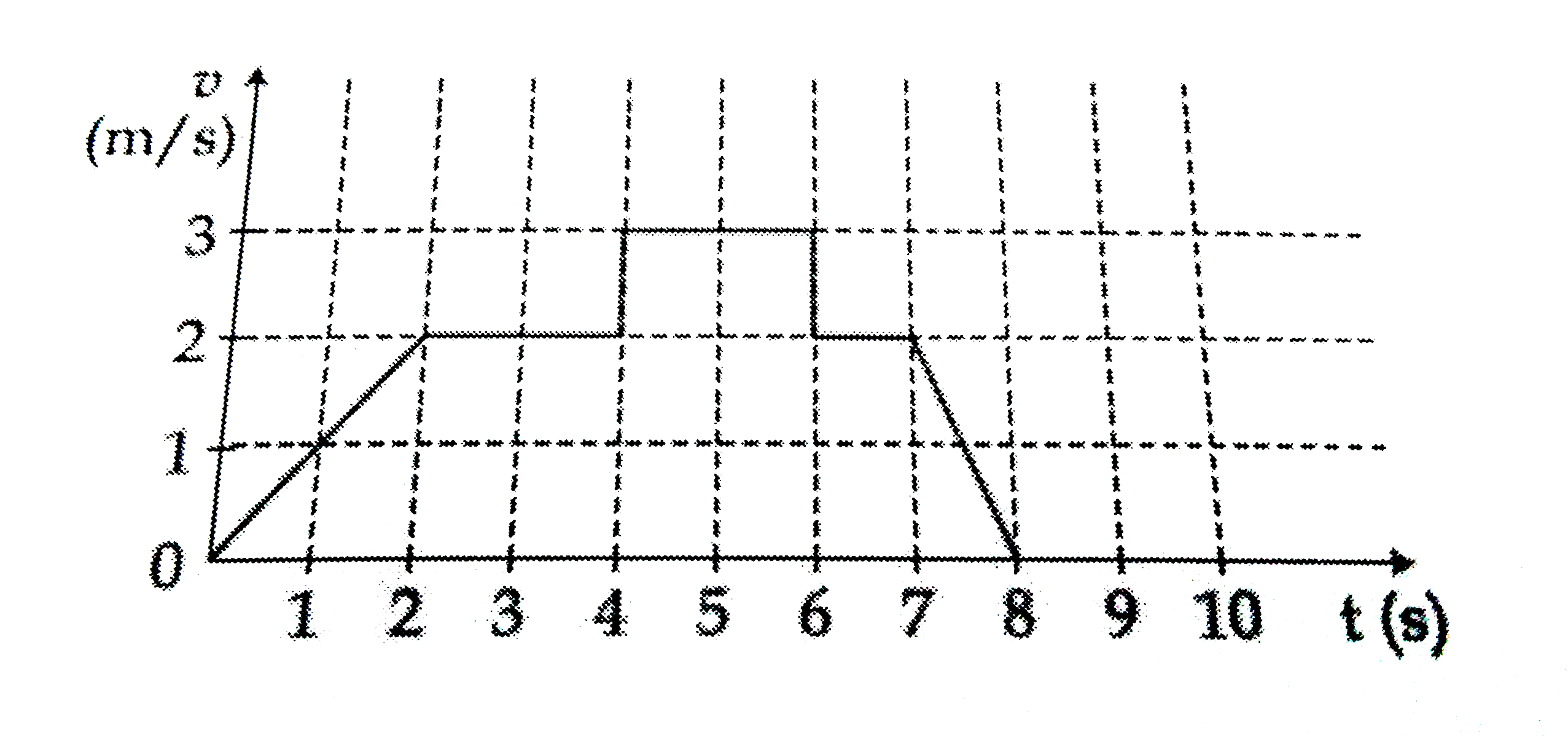
View SolutionA small particle of mass m is projected at an angle θ with x-axis with initial velocity υ0 in x-y plane as shown in Fig. Calculate the momentum of the particle
at t<υ0sinθg.

View SolutionIdentical 50μC charges are fixed on an x axis at x=+±2.0 m. A particle of charge q=15μC is then released from rest at a point on the positive part of they axis. Due to the symmetry of the situation, the particle moves along the y axis and has kinetic energy 1.2 J as it passes through the pointx=0,y=4.0m. (a) What is the kinetic energy of the particle as it passes through the origin? (b) At what negative value of y will the particle momentarily stop?
View Solution

