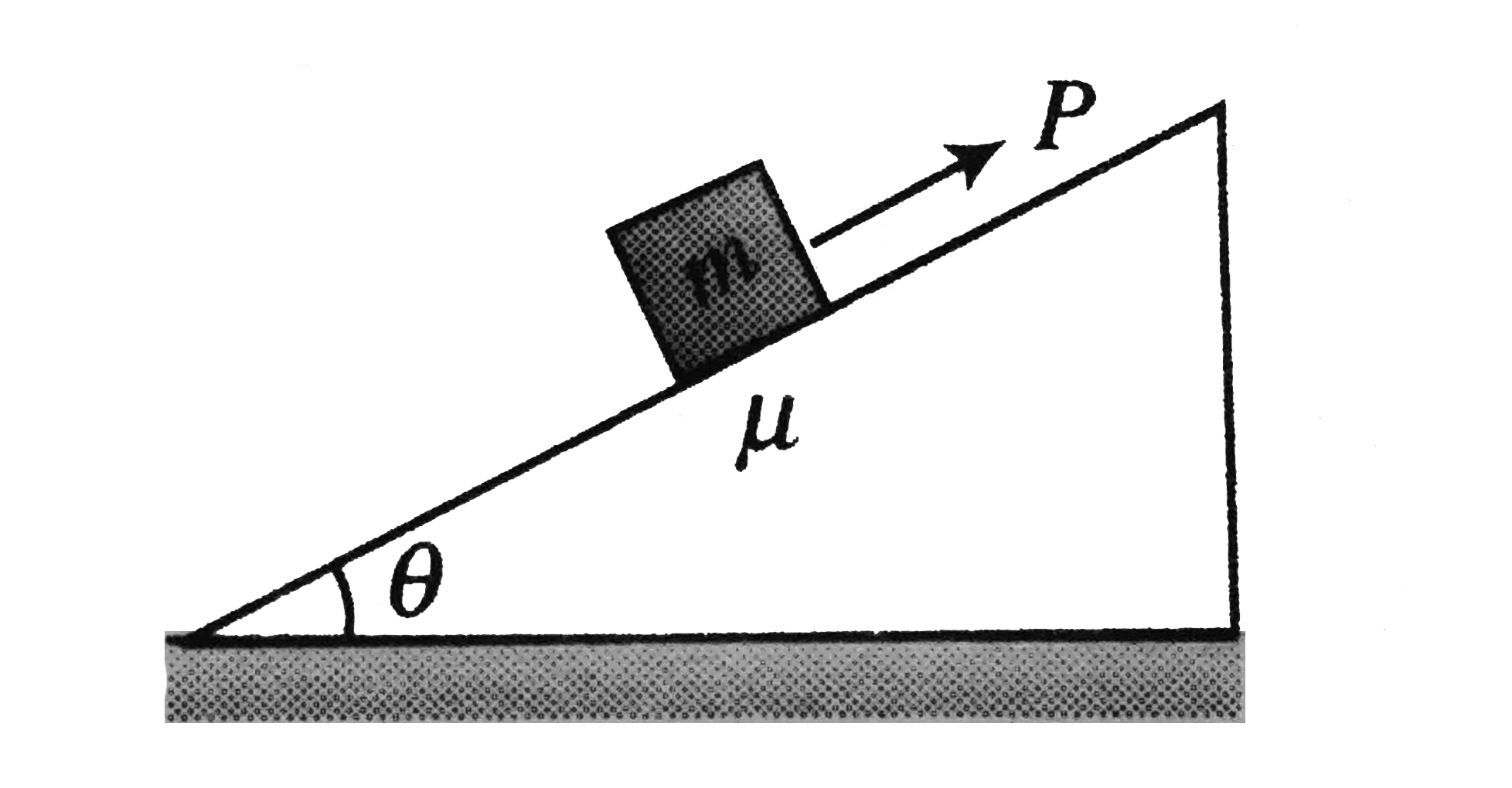
A block of mass m is being pulled up a rough incline by an agent delivering constant power P. The coefficient of friction between the block and the incline is μ. The maximum speed of the block during the course of ascent is
(a) Pmgsinθ+μmgcosθ
(b) Pmgsinθ−μmgcosθ
(c) 2Pmgsinθ−μmgcosθ
(d) 3Pmgsinθ−μmgcosθ
The correct Answer is:A
Let at any time, the speed of the block along the incline upwards be v.
Then from Newton's second law,
Pv−mgsinθ−μmgcosθ=mvdvdt
The speed is maximum when dvdt=0
vmax=Pmgsinθ+μmgcosθ
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Multiple Correct
Explore 25 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Linked Comprehension
Explore 55 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Subjective
Explore 23 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
Knowledge Check
A block of mass m is being pulled up the rough incline , inclined at angle θ with horizontal by an agent delivering constant power P. The coefficient of friction between block & incline is μ. Then during the upward motion along the inclined plane , maximum velocity of the block will be :
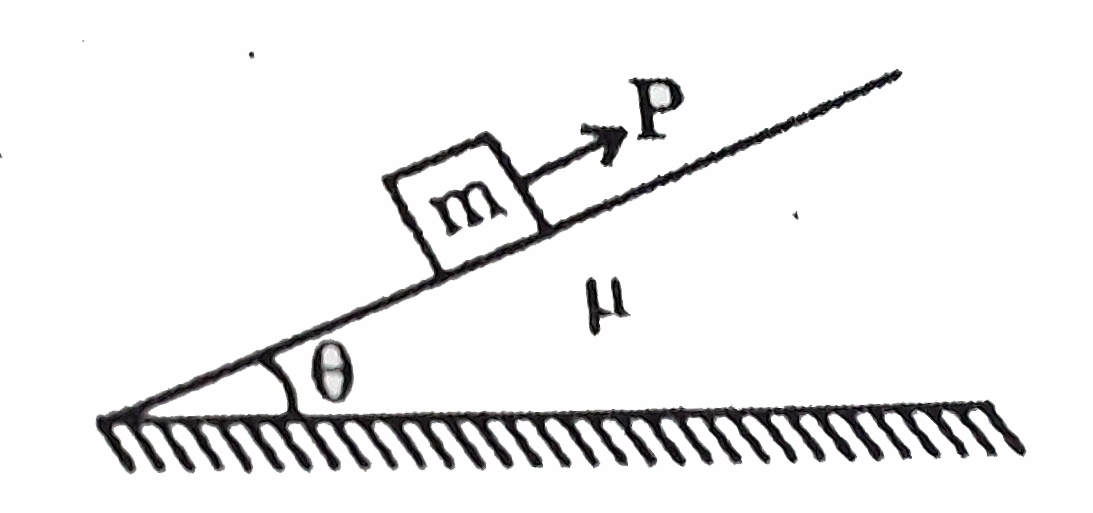 APmgsinθ+μ mgcosθBPmgsinθ−μ mgcosθCPmgsinθDPμmg sinθ
APmgsinθ+μ mgcosθBPmgsinθ−μ mgcosθCPmgsinθDPμmg sinθA block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θA block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
AmgcosθB√μ2+1mgcosθCμmgcosθ√μ2+1Dμmgθ
A block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
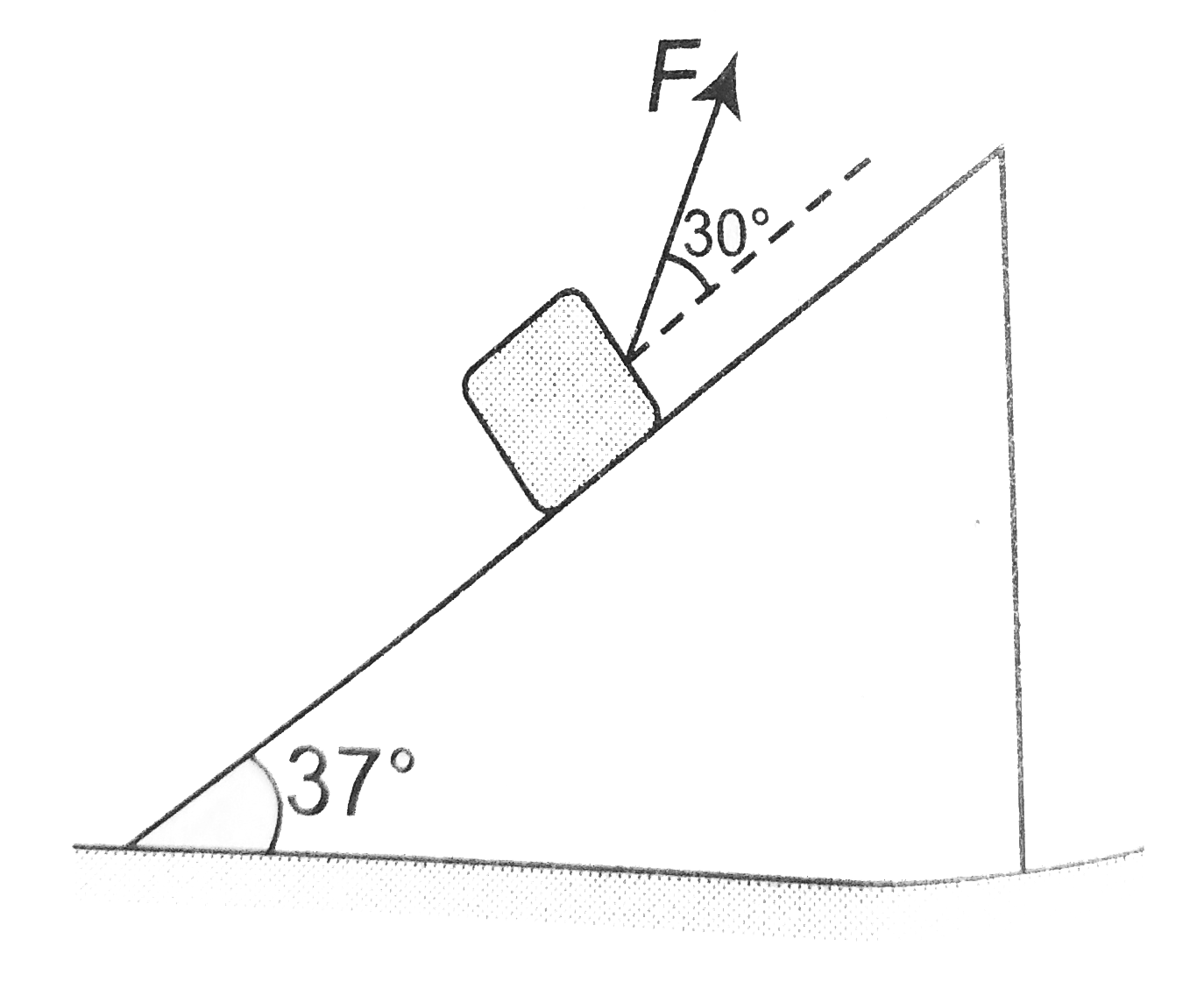
View SolutionA block of mass m=4kg is placed oner a rough inclined plane as shown in figure. The coefficient of friction between the block and the plane is μ=0.5 . A force F=10N is applied on the block at an angle of 30∘ .
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is .
View SolutionA block of mass m is placed on a rough inclined plane of inclination θ kept on the floor of the lift. The coefficient of friction between the block and the inclined plane is μ. With what acceleration will the block slide down the inclined plane when the lift falls freely ?
View Solution

