The potential energy for a force filed →F is given by U(x,y)=cos(x+y). The force acting on a particle at position given by coordinates (0,π/4) is
A
(a) −1√2(ˆi+ˆj)
B
(b) 1√2(ˆi+ˆj)
C
(c) (12ˆi+√32ˆj)
D
(d) (12ˆi−√32ˆj)
Video Solution
Text Solution
The correct Answer is:B
Fx=−∂U∂X=sin(x+y)=1√2
Fy=−∂U∂Y=sin(x+y)=1√2
→F=1√2[ˆi+ˆj]
|
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Multiple Correct
Explore 25 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Linked Comprehension
Explore 55 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Subjective
Explore 23 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
Knowledge Check
The potnetial energy for a force field →F is given by U(x,y)=cos(x+y). The force acting on a particle at the position given by coordinates (0,π/4) is
A−1√2(ˆi+ˆj)B1√2(ˆi+ˆj)C(12ˆi+√32ˆj)D(12ˆi−√32ˆj)The potential energy of a force filed →F is given by U(x,y)=sin(x+y). The force acting on the particle of mass m at (0,π4) is
A1B√2C1√2D0The potential energy of a force filed →F is given by U(x,y)=sin(x+y). The force acting on the particle of mass m at (0,π4) is
A1B√2C1√2D0
The potential energy of a particle varies with distance x as shown in the graph. The force acting on the particle is zero at
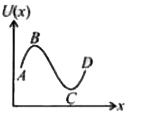
View SolutionThe potential energy of a particle varies with distance x as shown in the graph. The force acting on the particle is zero at

View SolutionThe potential energy of a particle oscillating on x-axis is given as U+20+(x−2)2. The mean position is at
View SolutionThe potential energy of a particle is given by formula U=100−5x+100x2,whereU and are .
View SolutionThe potential energy of a body is given by U=A−Bx2 (where x is the displacement). The magnitude of force acting on the partical is
View Solution

