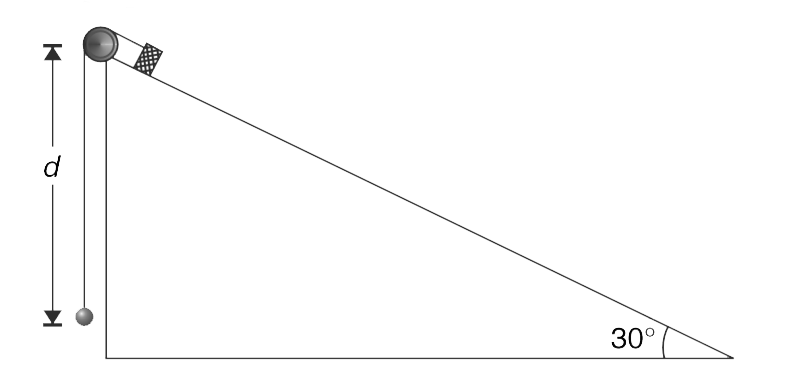
The blocks A and B shown in figure have masses MA=5kg and MB=4kg. The system is released from rest. The speed of B after A has travelled a distance 1m along the incline is
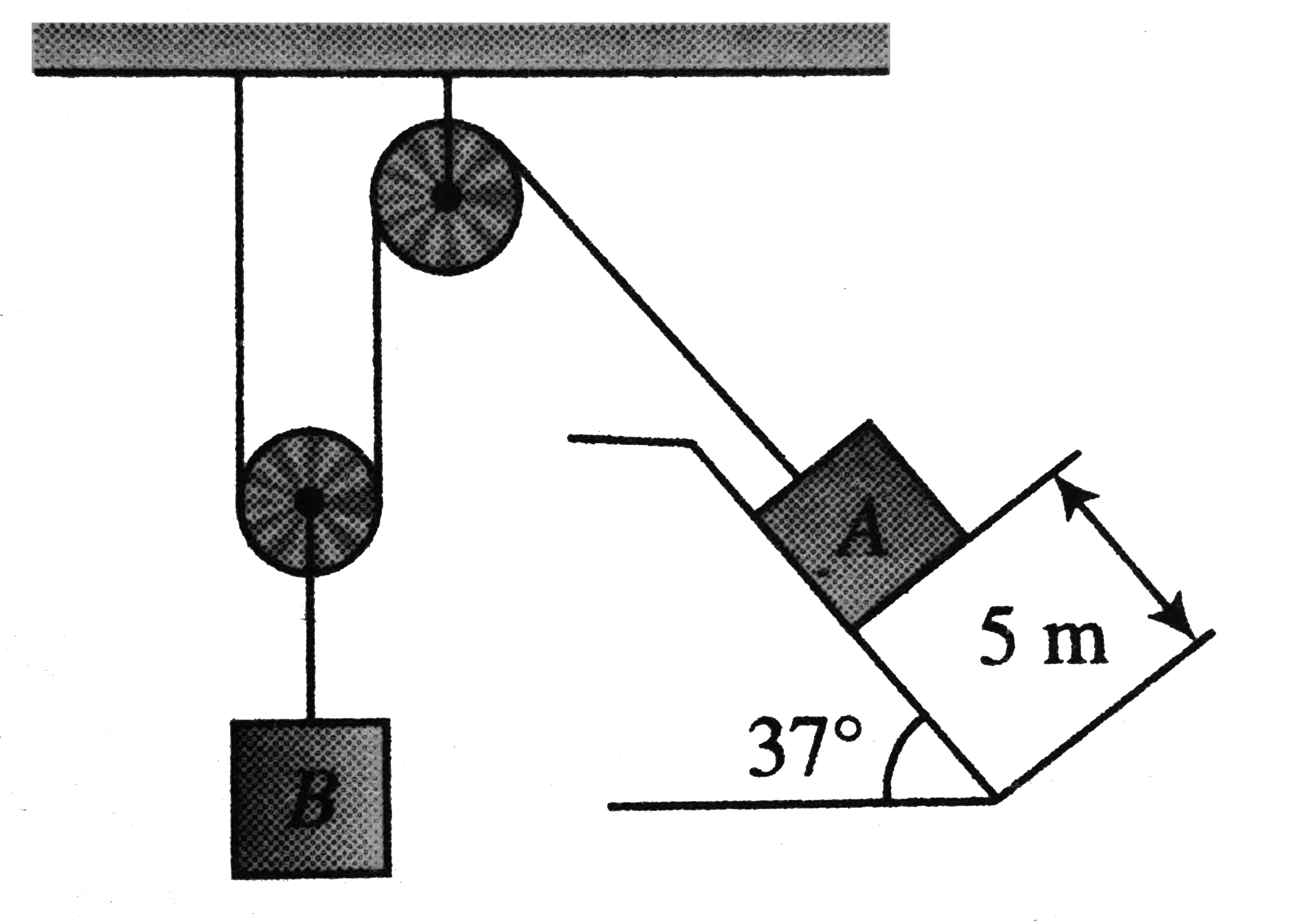
(a) √32√g
(b) √34√g
(c) √g2√3
(d) √g2
The correct Answer is:C
If A moves down the incline by 1m, B shall move up by 12m.
If the speed of B is v, then the speed of A will be 2v.
From conservation of energy,
Gain in KE=loss in PE
12mA(2v)2+12mBv2=mAg×35−mBg×12
Solving, we get
v=12√g3
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Multiple Correct
Explore 25 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Linked Comprehension
Explore 55 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Subjective
Explore 23 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
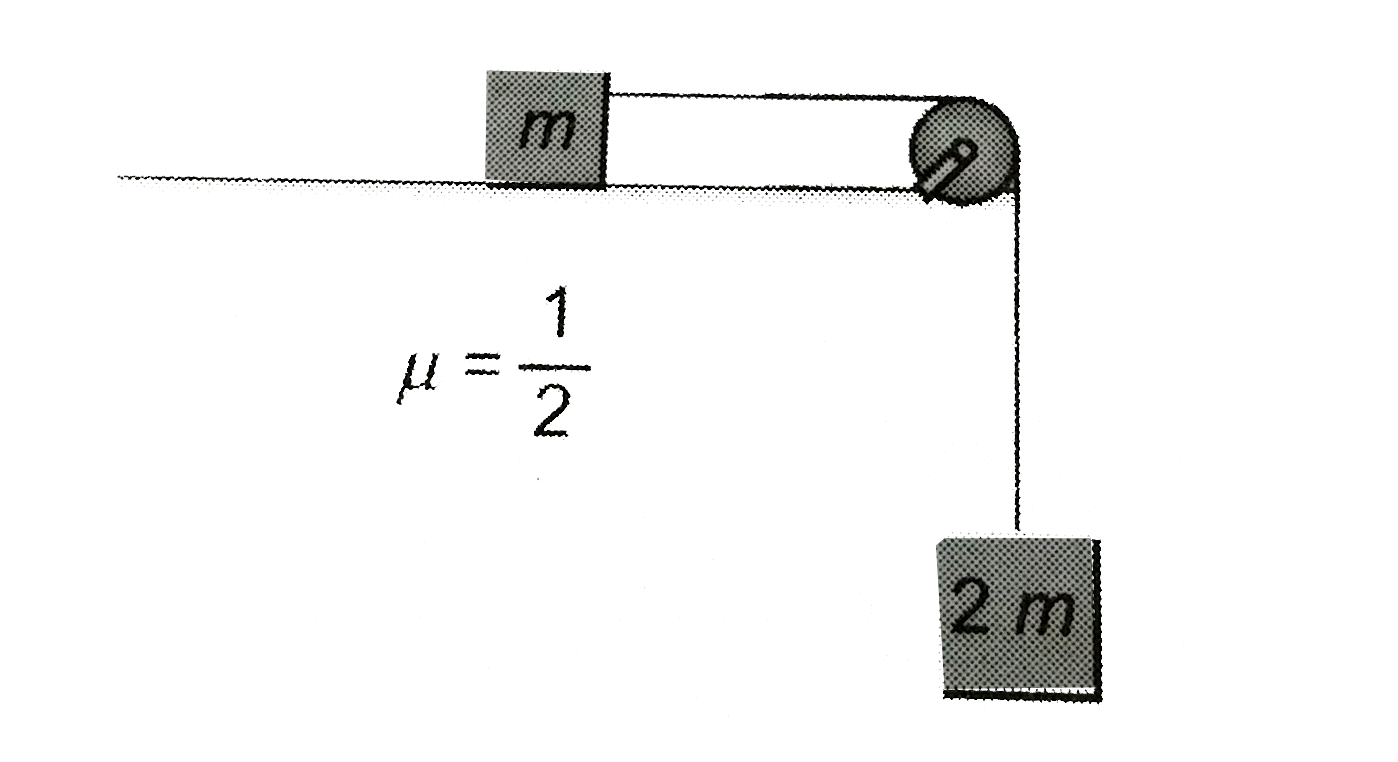
Consider the situation as shown in the figure. The system is released from rest. Find the speed of m when it has traveled a distance d on a rough surface.
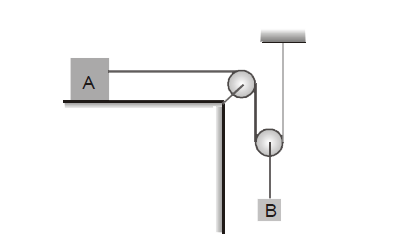
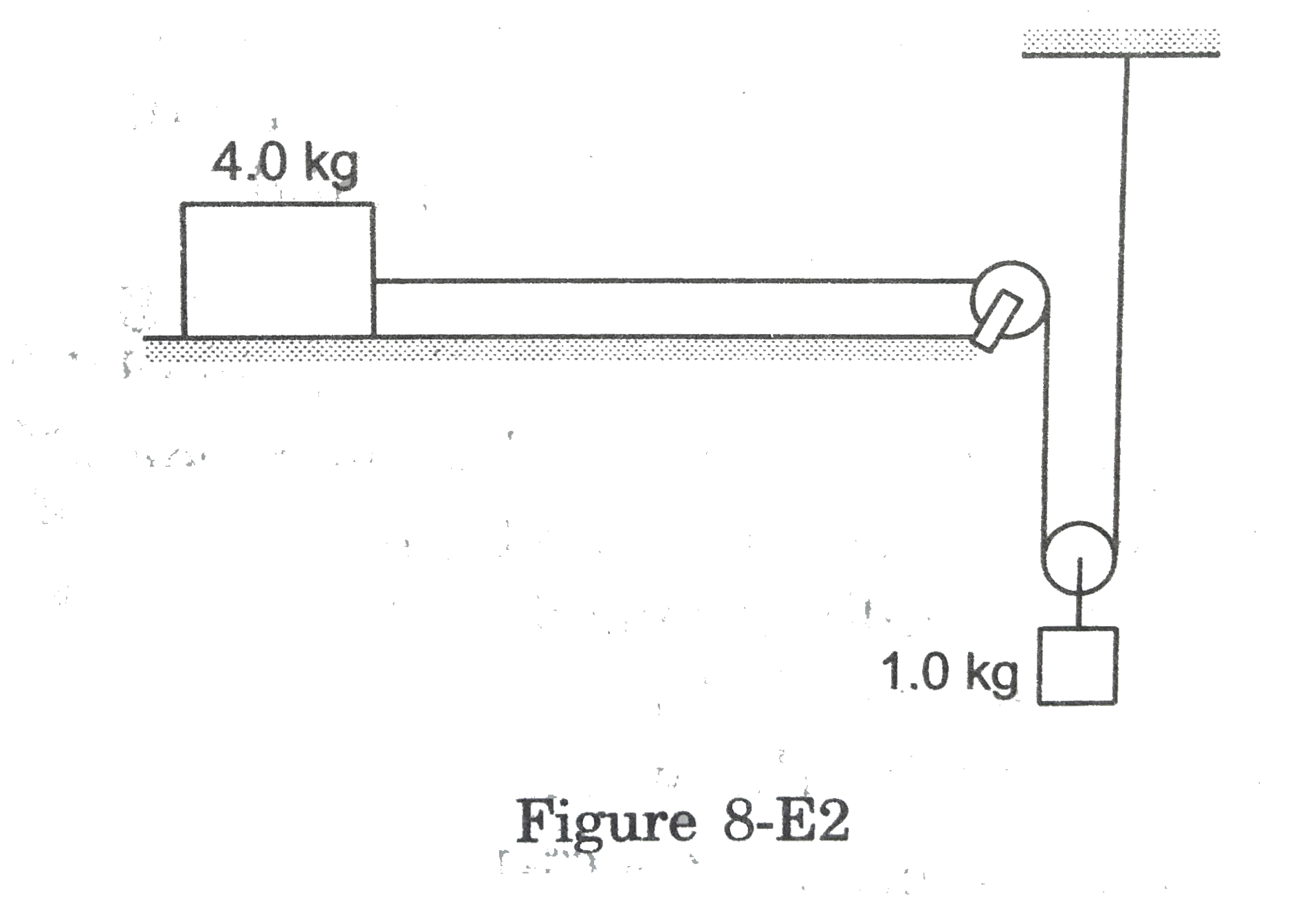
View SolutionIn the arrangement shown in figure mA = 4.0 kg and mB = 1.0 kg. The system is released from rest and block B is found to have a speed 0.3 m/s after it has descended through a distance of 1m. Find the coefficient of friction between the block and the table. Neglect friction elsewhere.
(Take g = 10 m/s2)
View Solution
Knowledge Check
A block of mass M is placed on the top of a bigger block of mass 10 M as shown in figure. All the surfaces are frictionless. The system is released from rest, then the distance moved by the bigger block at the instant the smaller block reaches the ground :
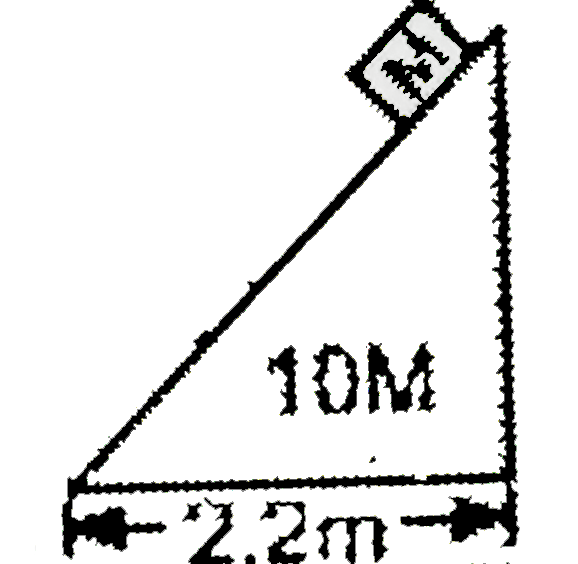 A0.22 mB0.20 mCzeroD0.24 m
A0.22 mB0.20 mCzeroD0.24 m
Blocks A and B shown in the figure are having equal masses m. The system is released from rest with the spring unstretched. The string between A and ground is cut, when there is maximum extension in the spring. The acceleration of centre of mass of the two blocks at this instant is
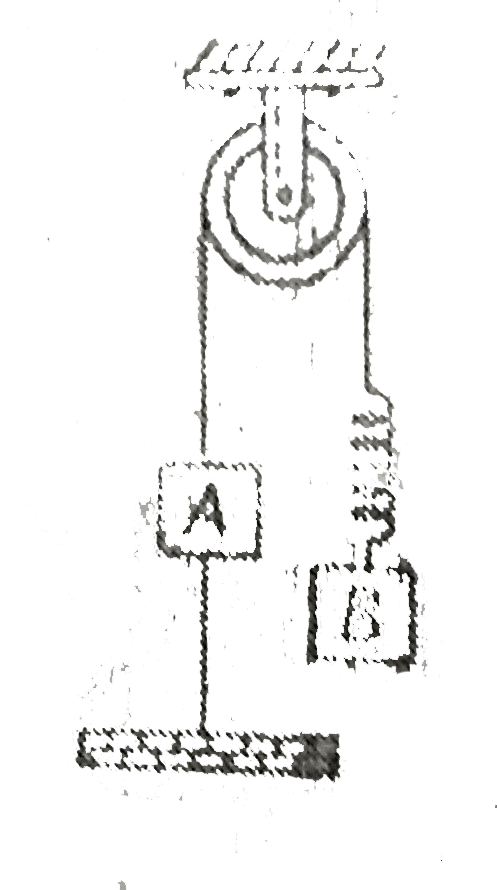
View SolutionIn the arrangement shown in figure mA = 4.0 kg and mB = 1.0 kg. The system is released from rest and block B is found to have a speed 0.3 m/s after it has descended through a distance of 1m. Find the coefficient of friction between the block and the table. Neglect friction elsewhere.
(Take g = 10 m/s2)

View SolutionConsider the situatioin shown in figure. The system is released from rest and the block of mass 1.0 kg is found to have a speed 0.3 m/s ater it has descended thrugh a distance of 1 m. find the coefficient of kinetic friction between the block and the table.
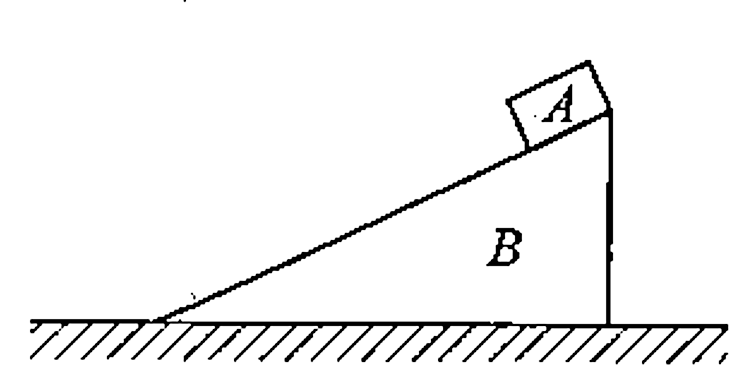
View SolutionA block A (mass 4M) is placed on the top of a wedge block B of base length l (mass=20M) as shown in figure. When the system is released from rest. Find the distance moved by the block B till the block A reaches ground Assume all surfaces are frictionless.
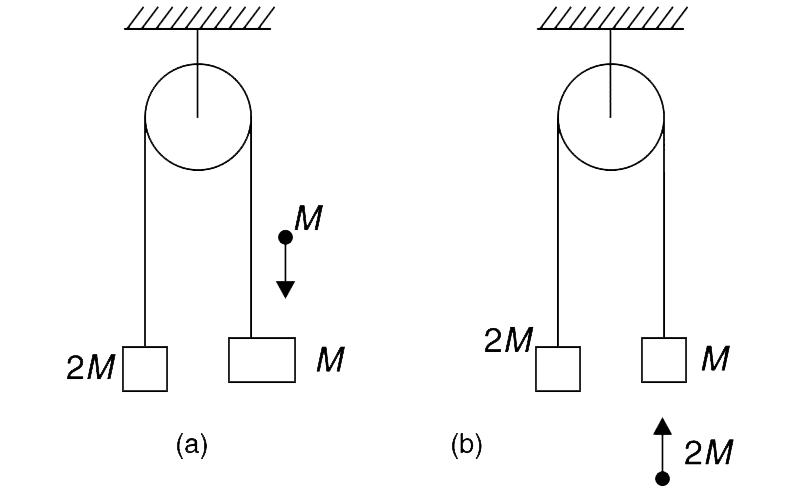
View SolutionTwo blocks of mass M and 2M are connected to the two ends of a light, inextensible string passing over an ideal pulley as shown in figure. The system is released from rest.
(a) One second after the system is released, a particle of mass M hits the block of mass M and sticks to it. The particle hits the block with a speed of 10 m/s while travelling downward. Find the total distance travelled by block of mass 2M after it is released.
(b) One second after the system is released, a particle of mass 2M hits the block of mass M and sticks to it. The particle hits the block with a speed of 10 m/s while travelling in upward direction. Find distance travelled by the block of mass 2M after it is released to the time it comes to rest for the first time (g=10m/s)2
View SolutionThe system shown in figure is held at rest. The boxes A and B have masses of 100 kg and 200 kg respectively. The inclined planes are smooth and long enough. The boxes are released to move. Find the speed (cm/s) of 100 kg box after it had travelled a distance of 6 cm.
View SolutionIn the system shown in fig, mass of the block is m1=4 kg and that of the hanging particle is m2=1 kg. The incline is fixed and surface is smooth. Block is initially held at the top of the incline and the particle hangs a distance d = 2.0 m below it. [Assume that the block and the particle are on same vertical line in this position]. System is released from this position. After what time will the distance between the block and the particle be minimum ? Find this minimum distance. [ g=10m/s2.]
View Solution

