In the system shown in fig, mass of the block is m1=4 kg and that of the hanging particle is m2=1 kg. The incline is fixed and surface is smooth. Block is initially held at the top of the incline and the particle hangs a distance d = 2.0 m below it. [Assume that the block and the particle are on same vertical line in this position]. System is released from this position. After what time will the distance between the block and the particle be minimum ? Find this minimum distance. [ g=10m/s2.]
![In the system shown in fig, mass of the block is m(1) = 4 kg and that of the hanging particle is m(2) = 1 kg. The incline is fixed and surface is smooth. Block is initially held at the top of the incline and the particle hangs a distance d = 2.0 m below it. [Assume that the block and the particle are on same vertical line in this position]. System is released from this position. After what time will the distance between the block and the particle be minimum ? Find this minimum distance. [ g = 10 m//s^(2).]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/IJA_PHY_V01_C03_E01_045_Q01.png)
The correct Answer is:1.0 s , 1.0 m
Step by step video, text & image solution for In the system shown in fig, mass of the block is m_(1) = 4 kg and that of the hanging particle is m_(2) = 1 kg. The incline is fixed and surface is smooth. Block is initially held at the top of the incline and the particle hangs a distance d = 2.0 m below it. [Assume that the block and the particle are on same vertical line in this position]. System is released from this position. After what time will the distance between the block and the particle be minimum ? Find this minimum distance. [ g = 10 m//s^(2).] by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
A block of mass m is released from the top of fixed inclined smooth plane. if theta is the angle of inclination then vertical accelertion of block is
View SolutionBlock A of mass m is placed over a wedge of same mass m. Both the block and wedge are placed on a fixed inclined plane. Assuming all surfaces to be smooth calculate the displacement of the block A in ground frame in 1s.
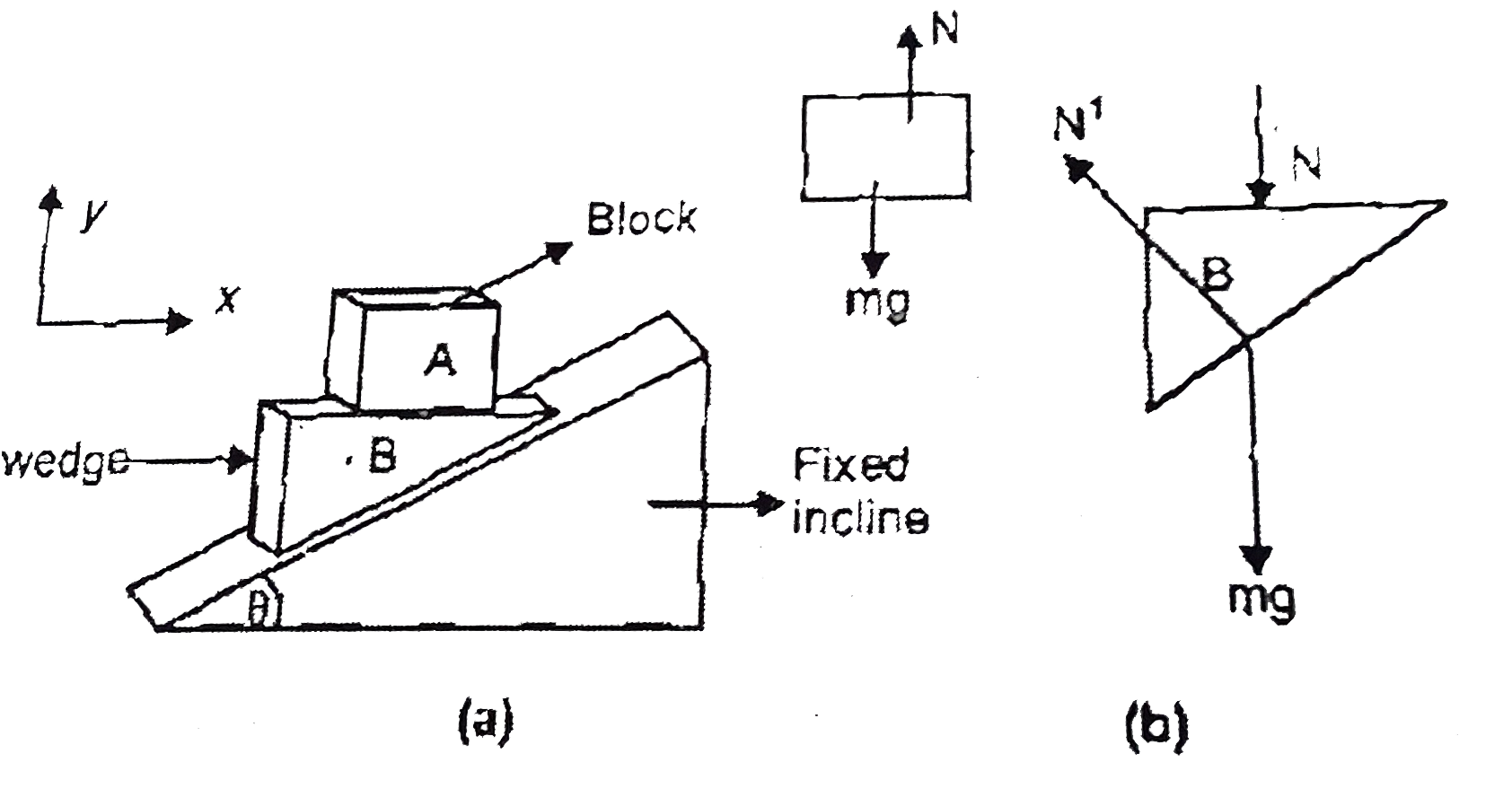
View Solution
Knowledge Check
- Question 1 - Select One
In the arrangement shown in fig. the block of mass m=2kg lies on the wedge of mass M=8kg. The initial acceleration of the wedge, if the surfaces are smooth, is
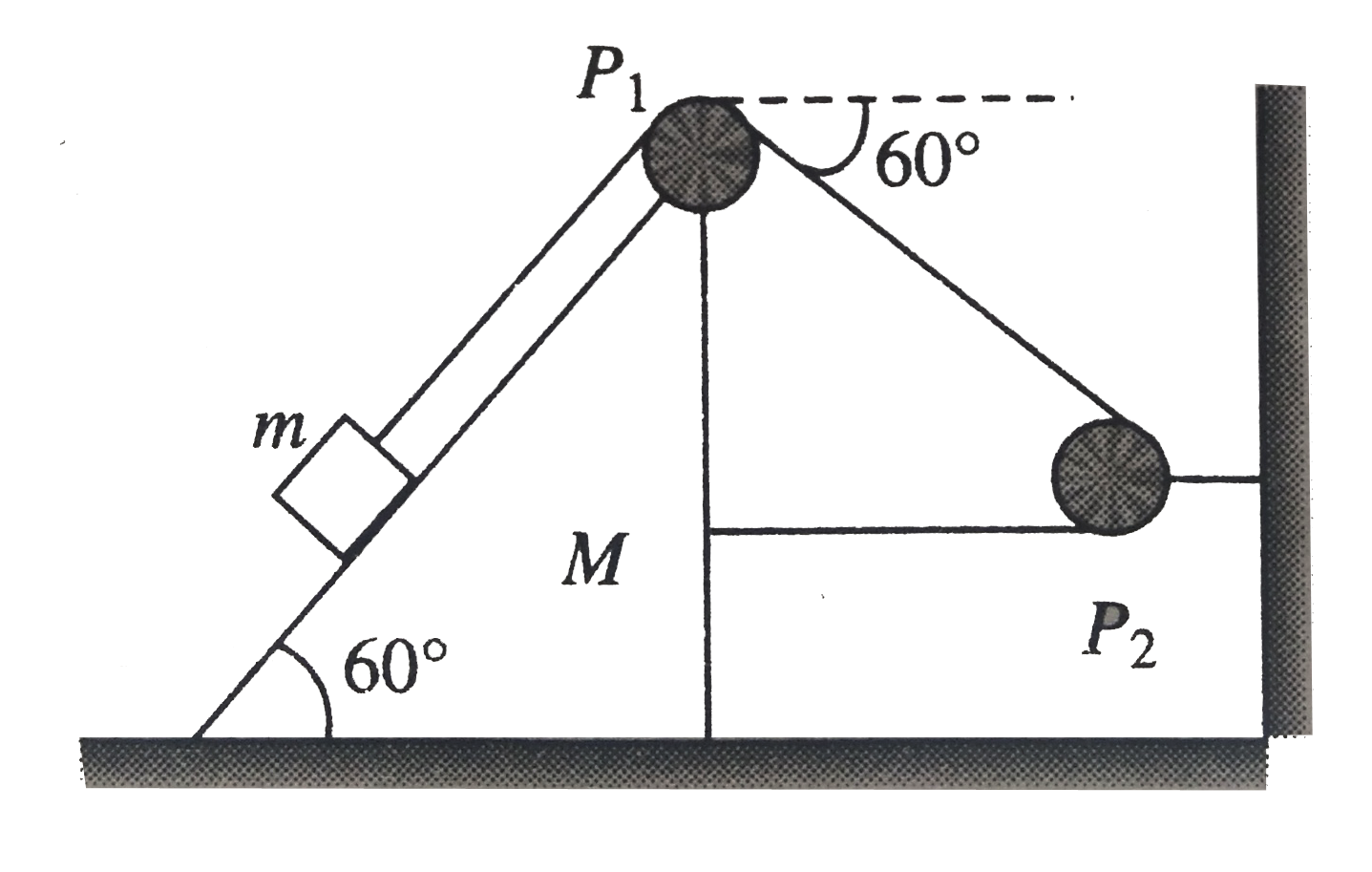A√3g23ms−2B3√3g23ms−2C3g23ms−2Dg23ms−2 - Question 2 - Select One
A smooth block of mass m is held stationary on a smooth wedge of mass M and inclination θ as shown in figure .If the system is released from rest , then the normal reaction between the block and the wedge is
AmgcosθBless than mgcosθCgreater than mgcosθDmay be less or greater than mgcosθ depending upon whether M is less or greater than m - Question 3 - Select One
The blocks A and B shown in figure have masses MA=5kg and MB=4kg. The system is released from rest. The speed of B after A has travelled a distance 1m along the incline is
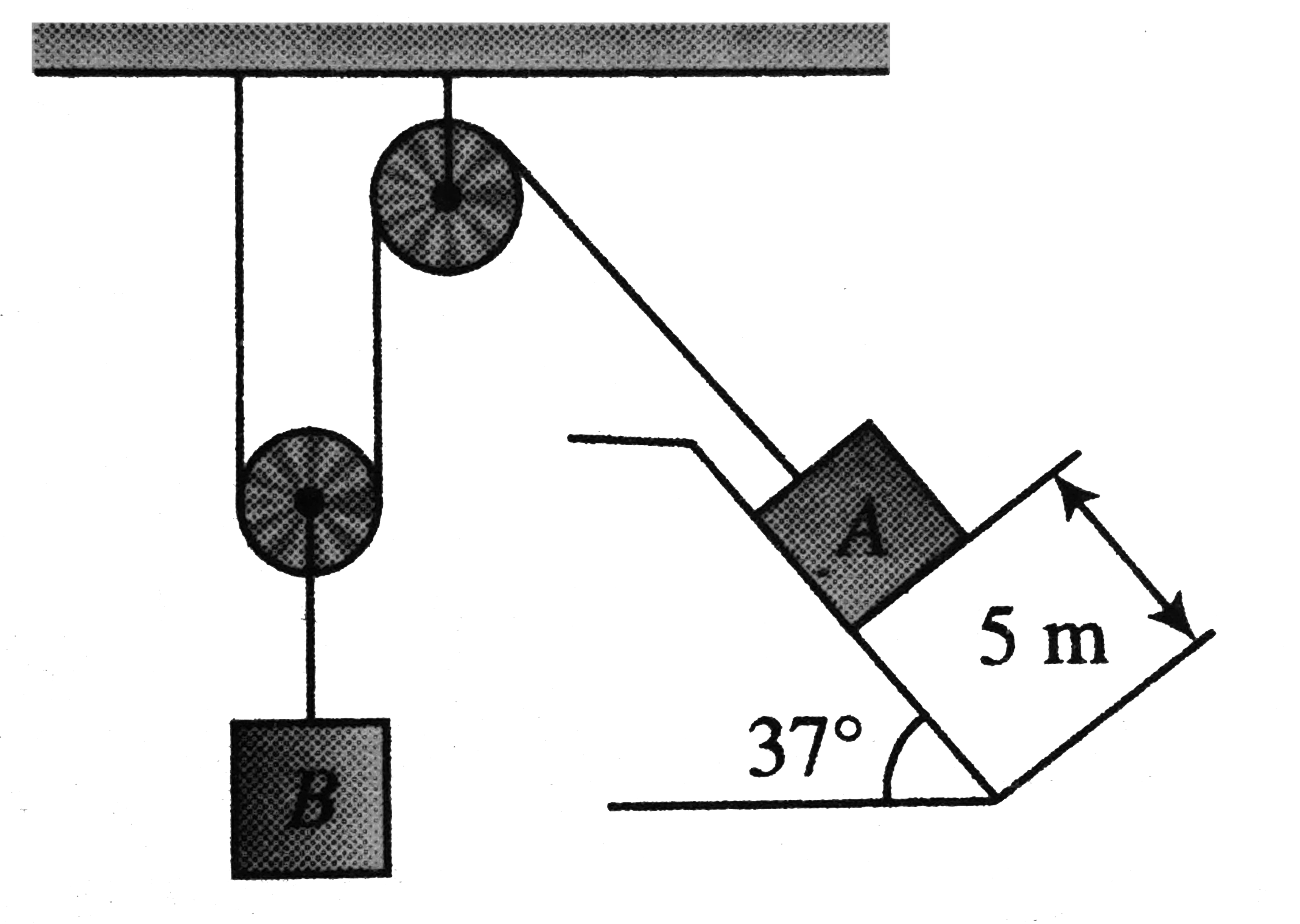A(a) √32√gB(b) √34√gC(c) √g2√3D(d) √g2
A 1 kg block sIides down an inclined plane of mass 3.2kg having inclination 45∘. If the inclined plane is fixed and the 1kg block slides without friction, find the acceleration of the centre of mass of the system of the block and inclined plane.
View SolutionIn the figure shown, the mass of the hanging block is m, while that of the black resting on the floor is 3m. The floor is horizontal and frictionless and all pulleys ideal. The system is initially held stationary with the inclined thread making an angle θ=30∘ with the horizontal. The blocks are now released from rest and allowed to move. the hanging block falls through a height (49.5) m before hitting the floor. it is found that the value of θ becomes 60∘, when the hanging block hits the floor. Find the speed with which the hanging block hits the floor.
View SolutionA block of mass 4kg is released from the top of a rough inclines plane of height 10m. If velocity of the block is10ms at the bottom of the inclined then work done by the friction force on the block will be
View SolutionIn figure m1=1kg and m2=4kg Find the mass m of the hanging block which will provent the smaller block from slipping over the triangular block .All the surface are frictionless and the string and the pulleys are light
View SolutionAn inclined plane is moving with Constant velocity v=4m/s on a horizoontal surface as shown in figure. If a block of mass 2kg is kept at top of the incline and their is no friction between the block and the incline, then the distance travelled by the incline till the block reaches bottom of the inclined is (g=10m/s2)
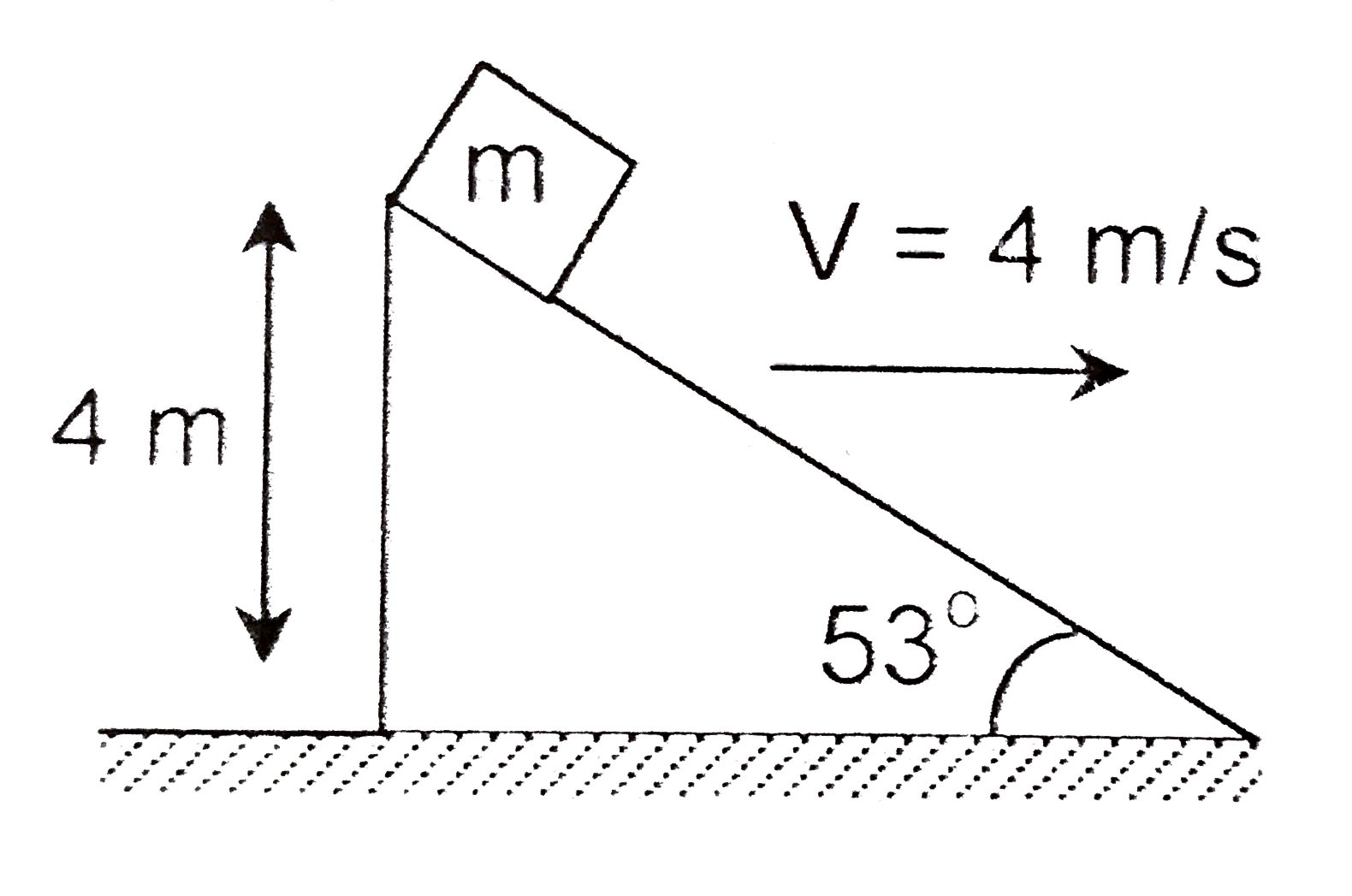
View Solution