If P and Q are the middle points of the sides BC and CD of the parallelogram ABCD, then AP+AQ is equal to
AC
12AC
23AC
32AC
The correct Answer is:D
AP=AB+BP=AB+12BC=AB+12AD . . . (i)
AQ=AD+DQ=AD+12DC=AD+12AB . . . (ii)
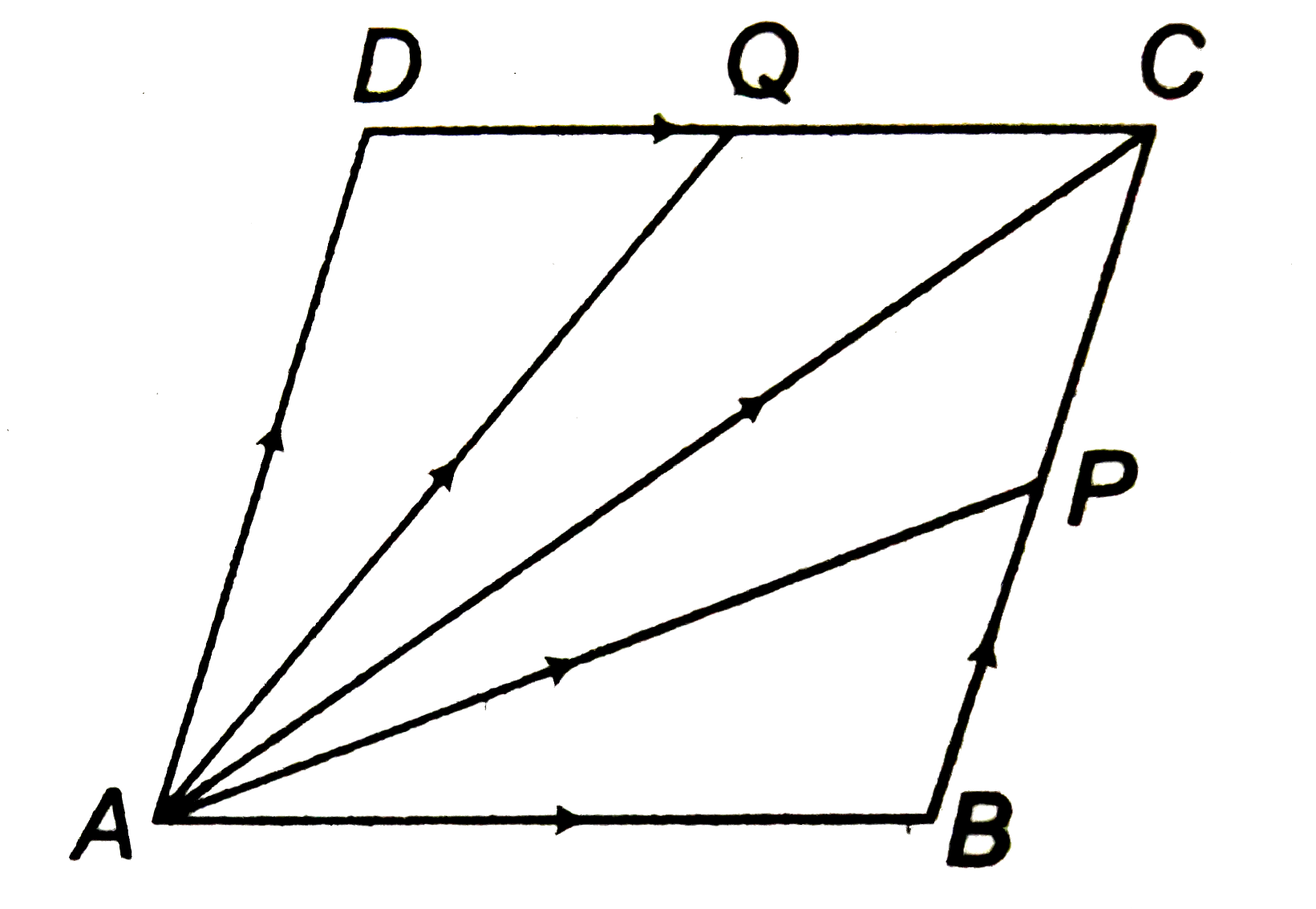
By eqs. (i) and (ii), we get
AP+AQ=32(AB+AD)
=32(AB+BC)=32AC.
Topper's Solved these Questions
- VECTOR ALGEBRABook:ARIHANT MATHSChapter:VECTOR ALGEBRAExercise:Exercise (More Than One Correct Option Type Questions)
Explore 7 Videos
- VECTOR ALGEBRABook:ARIHANT MATHSChapter:VECTOR ALGEBRAExercise:Exercise (Statement I And Ii Type Questions)
Explore 3 Videos
- VECTOR ALGEBRABook:ARIHANT MATHSChapter:VECTOR ALGEBRAExercise:Exercise For Session 3
Explore 11 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBook:ARIHANT MATHSChapter:TRIGONOMETRIC FUNCTIONS AND IDENTITIESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 19 Videos
Similar Questions
If P and Q are the mid points of the sides AB and CD of a parallelogram ABCD, prove that DP and BQ cut the diagonal AC in its points of trisection which are also the points of trisection of DP and BQ respectively.
View SolutionP and Q are the mid-point of the oposite sides AB and CD of a parallelogram ABCD. AQ interects DP at S and BQ interects CP at R. Show that PQRS is a parallelogram.

View Solution
Knowledge Check
In the given figure, M is the mid-point of the side CD of the parallelogram ABCD. What is ON:OB?
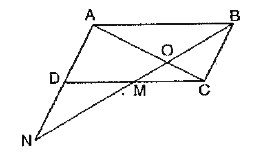 A3:2B2:1C3:1D5:2
A3:2B2:1C3:1D5:2ABCD is a parallelogram, E and F are the mid-points of BC and CD. Find the ratio of area of parallelogram ABCD and ΔAEF
A2:1B4:1C8:3D8:1
E and F are the mid-points of the sides AB and CD of a parallelogram ABCD. Prove that the line segment AF and CE trisects BD in three equal parts.
View SolutionThe middle points of the parallel sides AB and CD of a parallelogram ABCD are P and Q respectively. If AQ and CP divide the diagonal BD into three parts BX, XY and YD, then which one of the following is correct ?
View SolutionP and Q are points on opposite sides AD and BC of a parallelogram ABCD such that PQ passes through the point of intersection O of its diagonals AC and BD. Show that PQ is bisected at O.
View SolutionP, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
View SolutionP is the mid-point of the side AD of the parallelo- gram ABCD. The line BP meets the diagonal AC in Q and the line CD in R. Then RQ:QB is equal to
View SolutionPoints P and Q have been taken on opposite sides AB and CD, respectively of a parallelogram ABCD such that AP=CQ. Show that AC and PQ bisect each other.
View Solution

