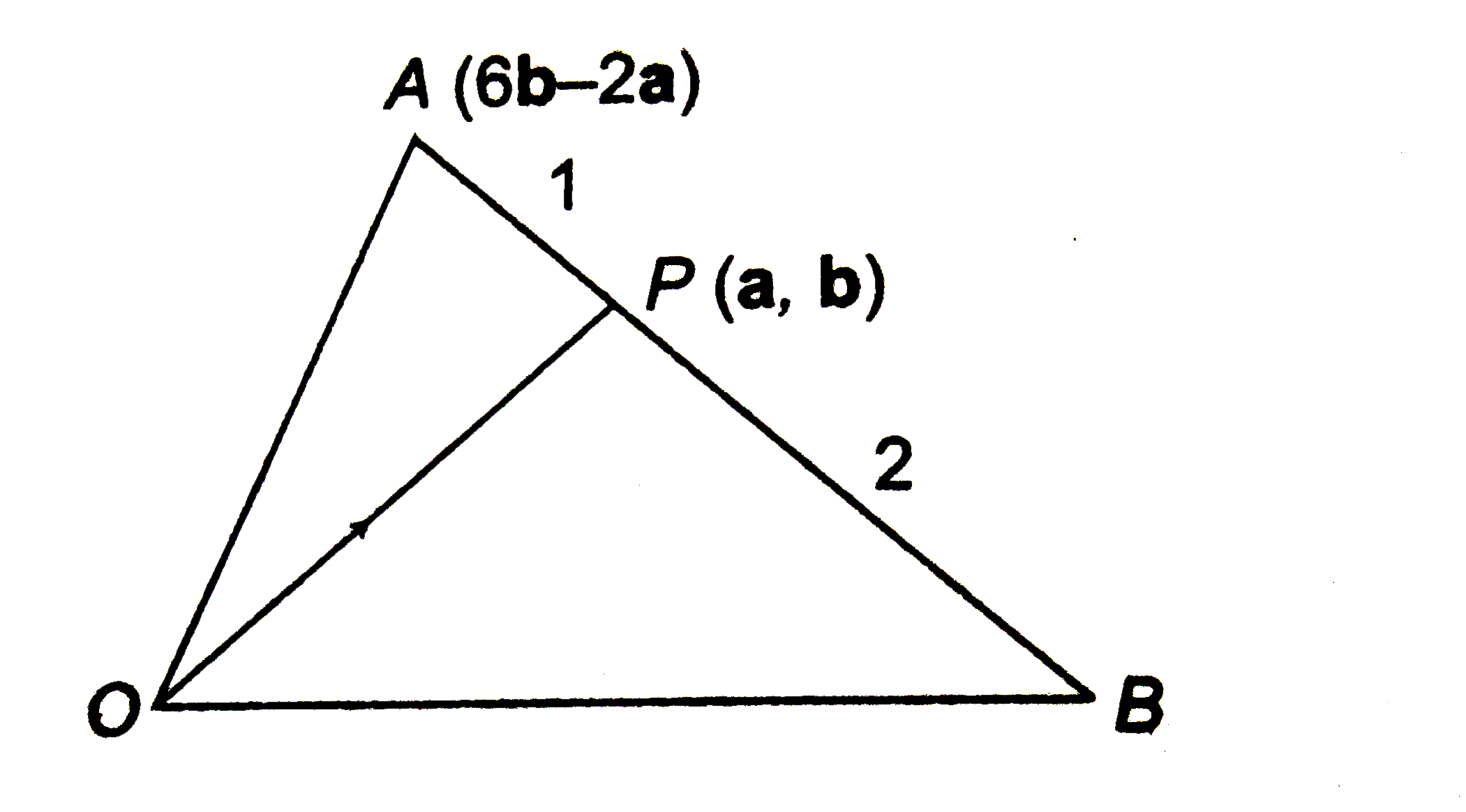
A and B are two points. The position vector of A is 6b-2a. A point P divides the line AB in the ratio 1:2. if a-b is the position vector of P, then the position vector of B is given by

7a-15b

7a+15b

15a-7b

15a+7b

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

If the position vector of p is $3 ¯ p + ¯ q and ¯ p$ divides PQ internally in the ratio $3 : 4$ , the position vector of $Q$ is
A $\frac{1}{3} (5 ¯ p + 4 ¯ q)$
B $\frac{1}{3} (4 ¯ p + 5 ¯ q)$
C $\frac{- 1}{3} (5 ¯ p + 4 ¯ q)$
D $\frac{- 1}{3} (4 ¯ p + 5 ¯ q)$
$¯ a, ¯ b$ are position vectors of points A and B. If P divides AB in the ratio $3 : 1$ and Q is the mid-point of AP, then position vectors of Q will be
A $\frac{1}{2} (¯ a - ¯ b)$
B $\frac{1}{2} (¯ a + ¯ b)$
C $\frac{1}{8} (5 ¯ a + 3 ¯ b)$
D $\frac{1}{8} (5 ¯ a - 3 ¯ b)$
If the position vector of a point A is $\to a + 2 \to b and \to a$ divides AB in the ratio $2 : 3$ , then the position vector of B, is
A $\to a - \to b$
B $\to b - 2 \to a$
C $\to a - 3 \to b$
D $\to b$