In a regular hexagon ABCDEF,¯¯¯¯¯¯AB+¯¯¯¯¯¯AC+¯¯¯¯¯¯AD+¯¯¯¯¯¯AE+¯¯¯¯¯¯AF=k¯¯¯¯¯¯AD then k is equal to
A
2
B
3
C
4
D
6
Video Solution
Text Solution
The correct Answer is:B
By triangle law, AB=AD−BD,AC=AD−CD
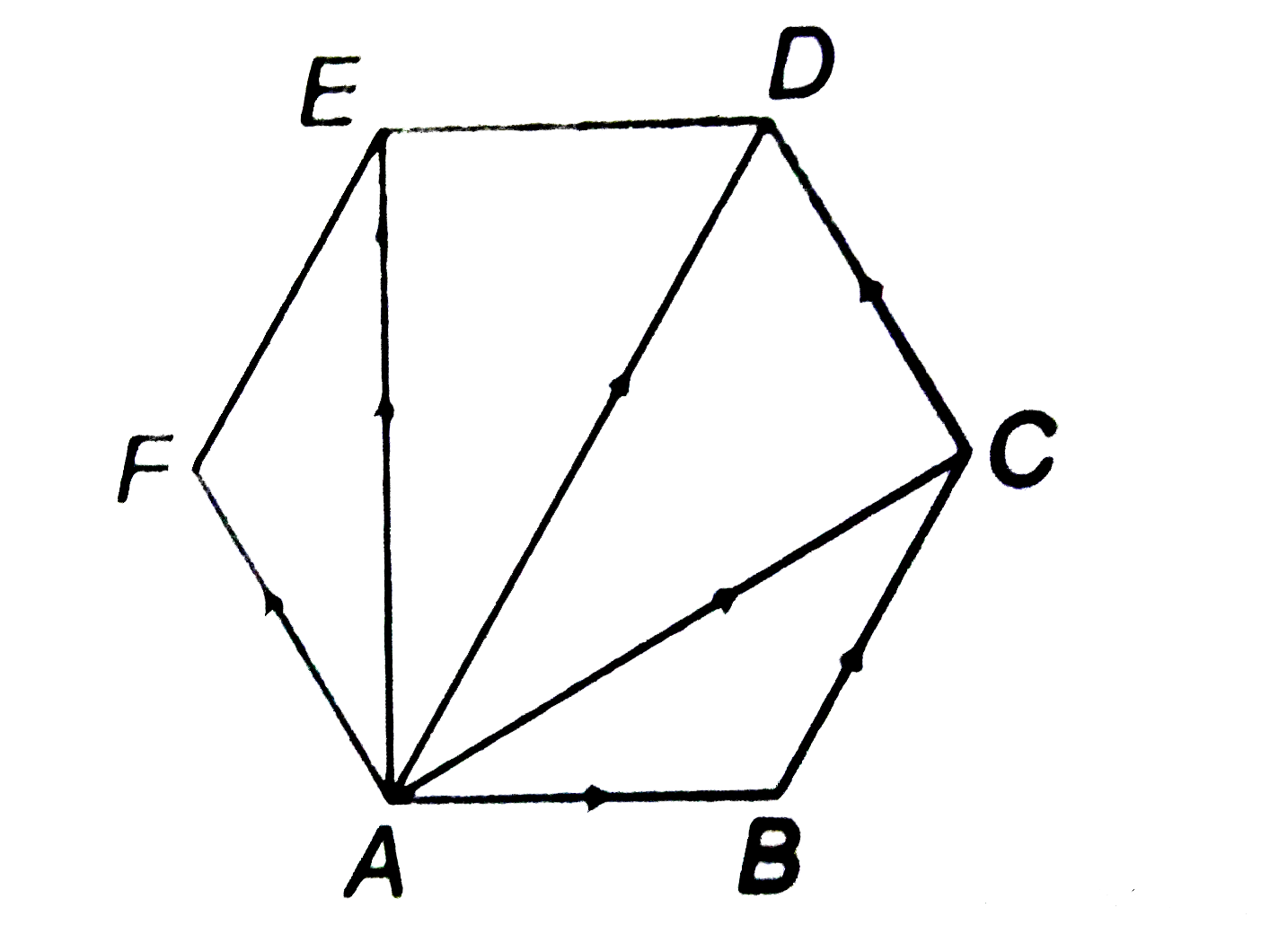
Therefore, AB+AC+AD+AE+AF
=3AD+(AE−BD)+(AF−CD)=3AD
hence, λ=3 (∵AE=BD,AF=CD)
|
Topper's Solved these Questions
- VECTOR ALGEBRABook:ARIHANT MATHSChapter:VECTOR ALGEBRAExercise:Exercise (More Than One Correct Option Type Questions)
Explore 7 Videos
- VECTOR ALGEBRABook:ARIHANT MATHSChapter:VECTOR ALGEBRAExercise:Exercise (Statement I And Ii Type Questions)
Explore 3 Videos
- VECTOR ALGEBRABook:ARIHANT MATHSChapter:VECTOR ALGEBRAExercise:Exercise For Session 3
Explore 11 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBook:ARIHANT MATHSChapter:TRIGONOMETRIC FUNCTIONS AND IDENTITIESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 19 Videos
Similar Questions
Knowledge Check
If ABCDEF is a regular hexagon , then
¯¯¯¯¯¯AB+¯¯¯¯¯¯AC+¯¯¯¯¯¯AE+¯¯¯¯¯¯AF =A4¯¯¯¯¯¯ADB3¯¯¯¯¯¯ADC2¯¯¯¯¯¯ADD¯¯¯¯¯¯ADIf ABCDEF is a regular hexagon, then ¯¯¯¯¯¯AC+¯¯¯¯¯¯AD+¯¯¯¯¯¯EA+¯¯¯¯¯¯FA=
A2¯¯¯¯¯¯ABB3¯¯¯¯¯¯ABC¯¯¯¯¯¯ABD¯0If ABCDEF is a regular hexagon and ¯¯¯¯¯¯AB=¯a then ¯¯¯¯¯¯AD+¯¯¯¯¯¯EB+¯¯¯¯¯¯FC=
A4¯aB14¯aC2¯aD12¯a
In a ΔABC,¯¯¯¯¯¯AB2+¯¯¯¯¯¯AC2=¯¯¯¯¯¯BC2 and ¯¯¯¯¯¯BC=√2¯¯¯¯¯¯AB , then ∠ABCis :
View SolutionIf ABCDE is a regular penatagon then :
¯¯¯¯¯¯AB+¯¯¯¯¯¯BC+¯¯¯¯¯¯AD+¯¯¯¯¯¯ED+¯¯¯¯¯¯AE=
View SolutionIf ABCDE is a pentagon, then ¯¯¯¯¯¯AB+¯¯¯¯¯¯AE+¯¯¯¯¯¯BC+¯¯¯¯¯¯DC+¯¯¯¯¯¯ED=
View SolutionIf PQRSTU is a regular hexagon such that
¯¯¯¯¯¯QR+¯¯¯¯¯¯QS+¯¯¯¯¯¯QP+¯¯¯¯¯¯QU=α¯¯¯¯¯¯QT, then : α=
View SolutionIn an octagon ABCDEFGH of equal side, what is the sum of ¯¯¯¯¯¯AB+¯¯¯¯¯¯AC+¯¯¯¯¯¯AD+¯¯¯¯¯¯AE+¯¯¯¯¯¯AF+¯¯¯¯¯¯AG+¯¯¯¯¯¯AH if ¯¯¯¯¯¯AO=2ˆi+3ˆj−4ˆk
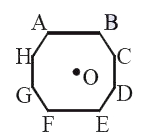
View Solution

