A,B,C and D have position vectors a,b,c and d, respectively, such that a-b=2(d-c). Then,
AB and CD bisect each other
BD and AC bisect each other
AB and CD trisect each other
BD and AC trisect each other
The correct Answer is:D
a−b=2(d−c)
∴a+2c2+1=b+2d2+1
Hence, AC and BD trisect each other as LHS is the position vector of a point trisecting A an C, and RHS that of B and D.
Topper's Solved these Questions
- VECTOR ALGEBRABook:ARIHANT MATHSChapter:VECTOR ALGEBRAExercise:Exercise (More Than One Correct Option Type Questions)
Explore 7 Videos
- VECTOR ALGEBRABook:ARIHANT MATHSChapter:VECTOR ALGEBRAExercise:Exercise (Statement I And Ii Type Questions)
Explore 3 Videos
- VECTOR ALGEBRABook:ARIHANT MATHSChapter:VECTOR ALGEBRAExercise:Exercise For Session 3
Explore 11 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBook:ARIHANT MATHSChapter:TRIGONOMETRIC FUNCTIONS AND IDENTITIESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 19 Videos
Similar Questions
A,B,CandD have position vectors →a,→b,→cand→d, respectively, such that →a−→b=2(→d−→c). Then a. ABandCD bisect each other b. BDandAC bisect each other c. ABandCD trisect each other d. BDandAC trisect each other
View SolutionA, B, C and D are four points in a plane with position vectors →a,→b,→cand→d, respectively, such that(→a−→d).(→b−→c)=(→b−→d).(→c−→a)=0 Then point D is the of triangle ABC
View Solution
Knowledge Check
If a, b, c, d are the position vectors of points A, B, C and D respectively such that
(a−d).(b−c)=(b−d).(c−a)=0
then D is theAcentroid of ΔABCBcircumcentre of ΔABCCorthocentre of ΔABCDnone of theseIf the points A,B,CandD have position vectors ¯a,2¯a+¯b,4¯a+2¯band5¯a+4¯b respectively, then three collinear points are
AA, B and CBA, C and DCA, B and DDB, C and D
A,B, C and D are respectively:ANa2PO4,NaPO3,MnNaPO4,MnOBNa2HPO4,NaPO3,MnNaPO4,MnOCNa3PO4,NaPO3,CuNaPO4,CuODNa2HPO4,NaPO3,CuNaPO4,CuO
Show that the found points A,B,C,D with position vectors →a,→b,→c,→d respectively such that 3 →a−2→b+5→c−6→d=→0 , are coplanar. Also, find the position vector of the point of intersection of the line segments AC and BD.
View SolutionIf →a,→b,→c are the position vectors of points A, B, C and D respectively such that (→a−→d)⋅(→b−→c)=(→b−→d)⋅(→c−→a)=0, then D is the
View Solution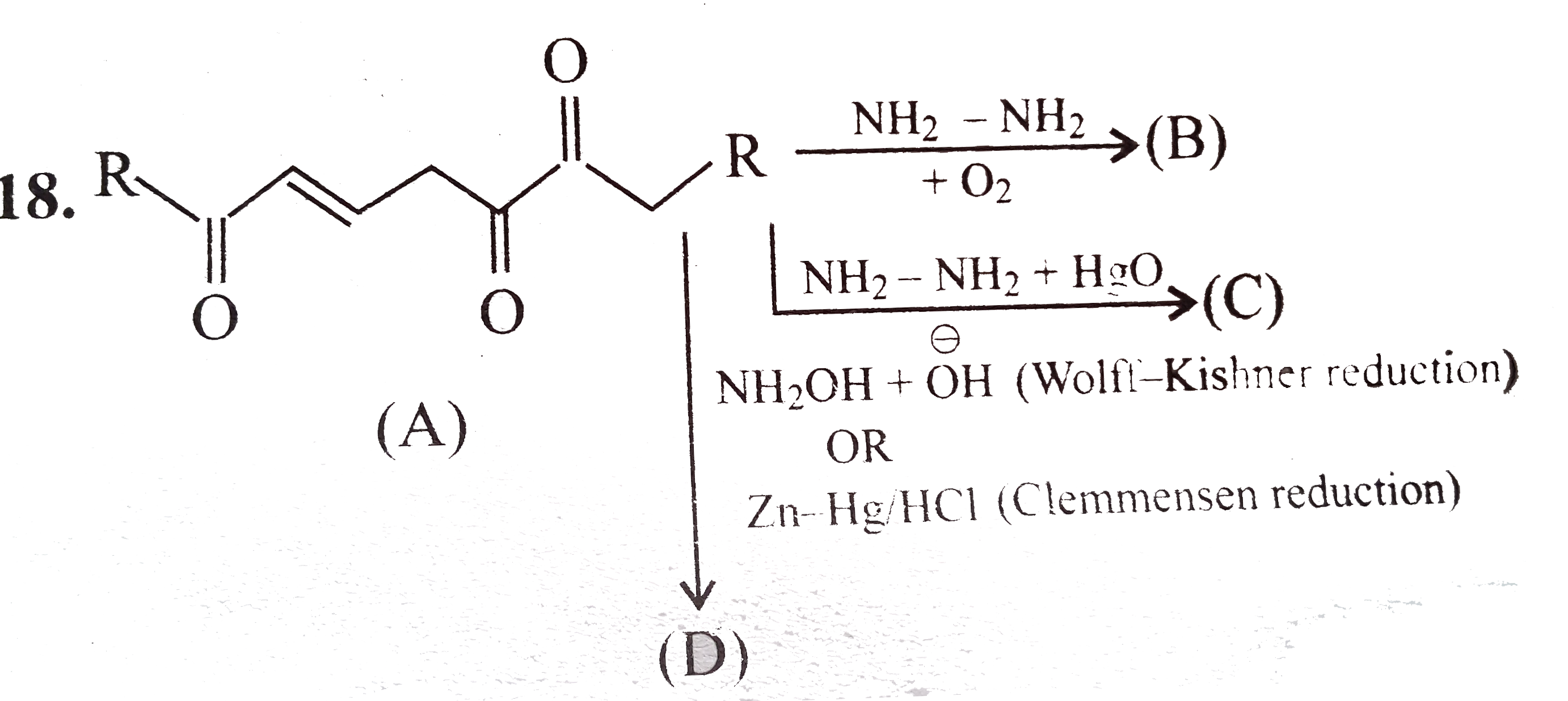
(B), (C), and (D), respectively, are
View SolutionThe position vector of four points A, B, C and D are a,b,c and d respectively . If a- b = 2(d-c) the
View SolutionThe position vector of four points A, B, C and D are a,b,c and d respectively . If a- b = 2(d-c) the
View Solution

