In a ΔABC,¯¯¯¯¯¯AB2+¯¯¯¯¯¯AC2=¯¯¯¯¯¯BC2 and ¯¯¯¯¯¯BC=√2¯¯¯¯¯¯AB , then ∠ABCis :
A)30∘
B)45∘
C)60∘
D)90∘
The correct Answer is:B
To solve the problem, we need to analyze the given information about triangle ABC.
1. Understanding the Given Information:
We are given that in triangle ABC, AB2+AC2=BC2 and BC=√2⋅AB.
2. Identifying the Type of Triangle:
The equation AB2+AC2=BC2 indicates that triangle ABC is a right triangle (by the Pythagorean theorem). The right angle is at vertex A.
3. Substituting the Lengths:
Let's denote AB=x. Then, from the second equation, we have:
BC=√2⋅x
4. Using the Pythagorean Theorem:
Since AB2+AC2=BC2, substituting the lengths we have:
x2+AC2=(√2⋅x)2
This simplifies to:
x2+AC2=2x2
5. Solving for AC:
Rearranging the equation gives:
AC2=2x2−x2=x2
Taking the square root of both sides, we find:
AC=x
6. Conclusion about the Triangle:
Since AB=AC=x, triangle ABC is an isosceles right triangle (with angles 45°-45°-90°).
7. Finding Angle ABC:
In an isosceles right triangle, the angles opposite the equal sides are equal. Therefore:
∠ABC=∠ACB=45∘
And since the angles in a triangle sum up to 180°, we have:
∠A+∠ABC+∠ACB=180∘
90∘+45∘+45∘=180∘
8. Final Answer:
Therefore, the angle ∠ABC is 45∘.
We are given that in triangle ABC, AB2+AC2=BC2 and BC=√2⋅AB.
The equation AB2+AC2=BC2 indicates that triangle ABC is a right triangle (by the Pythagorean theorem). The right angle is at vertex A.
Let's denote AB=x. Then, from the second equation, we have:
BC=√2⋅x
Since AB2+AC2=BC2, substituting the lengths we have:
x2+AC2=(√2⋅x)2
This simplifies to:
x2+AC2=2x2
Rearranging the equation gives:
AC2=2x2−x2=x2
Taking the square root of both sides, we find:
AC=x
Since AB=AC=x, triangle ABC is an isosceles right triangle (with angles 45°-45°-90°).
In an isosceles right triangle, the angles opposite the equal sides are equal. Therefore:
∠ABC=∠ACB=45∘
And since the angles in a triangle sum up to 180°, we have:
∠A+∠ABC+∠ACB=180∘
90∘+45∘+45∘=180∘
Therefore, the angle ∠ABC is 45∘.
Topper's Solved these Questions
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:TRY YOURSELF
Explore 25 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIII)
Explore 70 Videos
- DISCOUNTBook:KIRAN PUBLICATIONChapter:DISCOUNTExercise:Test Yourself
Explore 10 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
Similar Questions
Knowledge Check
If ABCDE is a pentagon, then ¯¯¯¯¯¯AB+¯¯¯¯¯¯AE+¯¯¯¯¯¯BC+¯¯¯¯¯¯DC+¯¯¯¯¯¯ED=
A¯¯¯¯¯¯ACB2¯¯¯¯¯¯ACC2¯¯¯¯¯¯ADD3¯¯¯¯¯¯ADIf ABCD is a square, then
¯¯¯¯¯¯AB+2¯¯¯¯¯¯BC+3¯¯¯¯¯¯CD+4¯¯¯¯¯¯DA =A4 ¯¯¯¯¯¯ACB3 ¯¯¯¯¯¯ACC2 ¯¯¯¯¯¯CAD¯¯¯¯¯¯ACIf ABCDEF is a regular hexagon , then
¯¯¯¯¯¯AB+¯¯¯¯¯¯AC+¯¯¯¯¯¯AE+¯¯¯¯¯¯AF =A4¯¯¯¯¯¯ADB3¯¯¯¯¯¯ADC2¯¯¯¯¯¯ADD¯¯¯¯¯¯AD
What is the angle between ?
(i) ¯¯¯¯¯¯ABand¯¯¯¯¯¯AC
(ii) ¯¯¯¯¯¯ABand¯¯¯¯¯¯BC
View SolutionABCDE is a regular hexagon. i) If ¯¯¯¯¯¯AB+¯¯¯¯¯¯AE+¯¯¯¯¯¯BC+¯¯¯¯¯¯DC+¯¯¯¯¯¯ED+¯¯¯¯¯¯AC=λ¯¯¯¯¯¯AC then λ=
View SolutionIn the figure 11.34, ABCD is a quadrilateral in which ¯¯¯¯¯¯AB=¯¯¯¯¯¯ADand¯¯¯¯¯¯BC=¯¯¯¯¯¯DC. Diagonals ¯¯¯¯¯¯ACandBD intersect each other at O.Show that-
View SolutionTriangles ABC and ABD are isosceles with AB=AC=BD,and¯¯¯¯¯¯BD intersects ¯¯¯¯¯¯AC at E. If ¯¯¯¯¯¯BD⊥¯¯¯¯¯¯AC then ∠C+∠D is
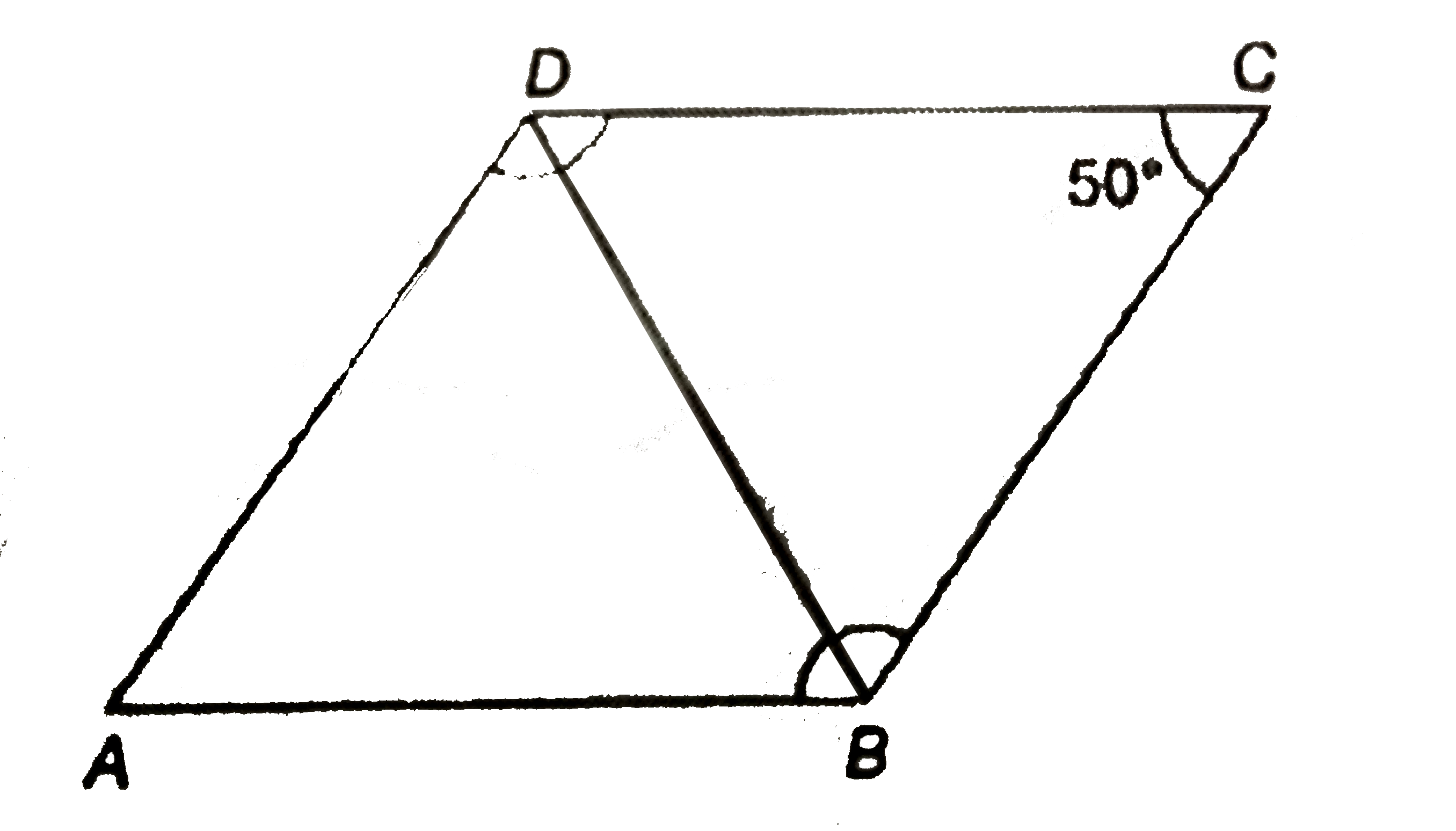
View SolutionIn the figure, ABD, BCD are two triangles. BD is the bisector of ∠ABCand∠ADC.¯¯¯¯¯¯AB || ¯¯¯¯¯¯CDand¯¯¯¯¯¯AD || ¯¯¯¯¯¯BC. If ∠BCD=50∘, then find the angle of ∠BAD.
View Solution
