Question

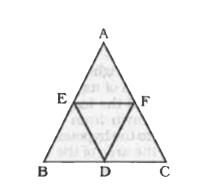
If D, E and Fare the mid points of BC, CA and AB respectively of the ABC then the ratio of area of the parallelogram DEFB and area of the trapezlum CAFD is:

Options

A. `2:3`
B. `3:4`
C. `1:2`
D. `1:3`

Answer

A

Explanation

To solve the problem of finding the ratio of the area of the parallelogram DEFB to the area of the trapezium CAFD in triangle ABC, we can follow these steps:

1. Identify the Midpoints:
Let D, E, and F be the midpoints of sides BC, CA, and AB of triangle ABC, respectively.

2. Understanding the Parallelogram:
Since D and E are midpoints, line segment DE is parallel to side AB and is half its length (by the midpoint theorem). Similarly, line segment FB is parallel to side AC and is half its length. Thus, DEFB forms a parallelogram.

3. Area of Parallelogram DEFB:
The area of parallelogram DEFB can be expressed in terms of the areas of triangles formed within the triangle ABC. Since DEFB is made up of two triangles (BDF and FED), we can denote the area of each triangle as X. Therefore, the total area of parallelogram DEFB is:
\( \text{Area of DEFB} = 2X \)

4. Understanding the Trapezium:
The trapezium CAFD consists of triangles AEF and CDF. The area of triangle AEF can be denoted as X and the area of triangle CDF can also be denoted as X. Additionally, triangle DEF (which is also part of CAFD) has an area of X. Thus, the total area of trapezium CAFD is:
\( \text{Area of CAFD} = 3X \)

5. Finding the Ratio:
Now, we can find the ratio of the area of parallelogram DEFB to the area of trapezium CAFD:
\( \text{Ratio} = \frac{\text{Area of DEFB}}{\text{Area of CAFD}} = \frac{2X}{3X} = \frac{2}{3} \)

6. Final Ratio:
Therefore, the ratio of the area of parallelogram DEFB to the area of trapezium CAFD is:
\( 2:3 \)