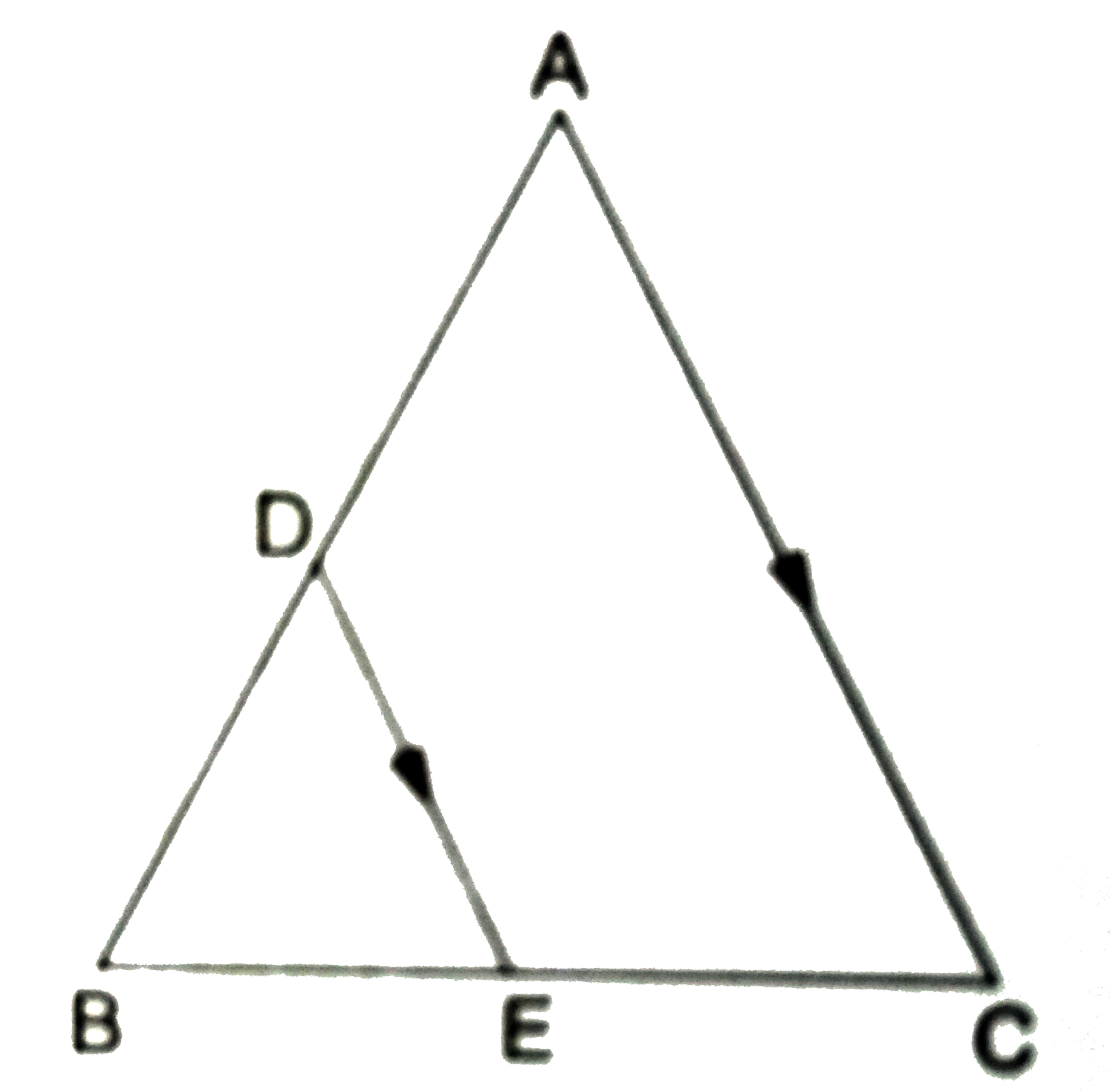
In $Δ A B C, D and E$ are the midpoint of AB and AC respectively. Find the ratio of the areas of $Δ A D E and Δ A B C$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $1 : 4$

Clearly $D E ∣ ∣ B C$ .
$∴ Δ A D E ~ Δ A B C$ .
$∴ \frac{a r (Δ A D E)}{a r (Δ A B C)} = \frac{A D^{2}}{A B^{2}} = \frac{A D^{2}}{{(2 A D)}^{2}} = \frac{1}{4}$

|

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Topper's Solved these Questions

BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7D
22videos
TRIANGLES
BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7E
30videos
TRIANGLES
BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7B
19videos
TRIANGLES
BOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27videos
T-RATIOS OF SOME PARTICULAR ANGLES
BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20videos
TRIGONOMETRIC IDENTITIES

Similar Questions

Knowledge Check

Question 1 - Select One
ABC is a triangle and D,E,F are the mid-points of the sides BC,CA, AB respectively . The ratio of the areas of $Δ A B C and Δ D E F$ is :
A4:1
B5:1
C3:1
Dcan't be determind
Question 2 - Select One
ABC is a triangle and D,E,F are the mid-points of the sides BC,CA, AB respectively . The ratio of the areas of $Δ A B C and Δ D E F$ is :
A $4 : 1$
B $5 : 1$
C $3 : 1$
Dcan't be determined
Question 3 - Select One
$Δ A B C$ is an equilateral triangle and D and E are midpoints of AB and BC respectively. Then the area of $Δ A B C$ : the area of the trapezium ADEC is
A $5 : 3$
B $4 : 1$
C $8 : 5$
D $4 : 3$

RS AGGARWAL-TRIANGLES-Exercise 7C

Home
Ask Doubt
Profile