ΔABC is right-angled at A and AD⊥BC. If BC=13cmandAC=5cm, find the ratio of areas of ΔABCandΔADC.

Video Solution
Text Solution
The correct Answer is:169:25
In ΔBACandΔADC, we have
∠BAC=∠ADC=90∘
and∠ACB=∠DCA=∠C
∴ΔBAC~ΔADC. [ by AA-similarity]
∴ar(ΔABC)ar(ΔADC)=ar(ΔBAC)ar(ΔADC)=BC2AC2
|
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7D
22 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7E
30 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7B
19 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
Knowledge Check
△ABC is a right angled at A and AD is the altitude to BC. If AB= 7 cm and AC = 24 cm. Find the ratio of AD is to AM if M is the mid-point of BC.
A25:41B32:41C336/625D625/336ΔABC is right-angled at C. If AC=5cmandBC=12cm find the length of AB.
A17B7C13D14ABC is a triangle in which ∠A=90∘ , AN⊥BC, BC=12 cm and AC=5 cm. Find the ratio of the areas of △ANC and △ABC.
A125:44B25:144C144:25D12:5
In ΔABC,AB=6cm,BC=7cm and AC=5cm .The area of ΔABC is
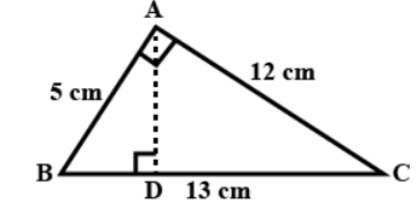
View SolutionΔABC is right angled at A (Fig 11.25). AD is perpendicular to BC. If AB=5cm,BC=13 and, find the area of ΔABC Also find the lenght of AD.
View SolutionABC is a right angled triangle AB = 3 cm, BC = 5 cm and AC = 4 cm, then the inradius of the circle is :

View SolutionABC is a right angled triangle AB = 3 cm, BC = 5 cm and AC = 4 cm, then the inradius of the circle is :

View SolutionABC is a right angled triangle AB = 3 cm, BC = 5 cm and AC = 4 cm, then the inradius of the circle is :
View Solution
