Two line segments PQ and RS intersect at X in such a way that XP=XR. If ∠PSX=∠RQX, then one must have
PR=QS
PS=RQ
∠XSQ=∠XRP
ar(ΔPXR)=ar(ΔQXS)
The correct Answer is:B
To solve the problem, we need to analyze the given information about the line segments PQ and RS that intersect at point X, with the conditions that XP=XR and ∠PSX=∠RQX.
1. Identify the Given Information:
- We have two line segments PQ and RS intersecting at point X.
- The lengths of the segments are equal: XP=XR.
- The angles formed at point X are equal: ∠PSX=∠RQX.
2. Draw the Diagram:
- Draw two intersecting lines, one representing line segment PQ and the other representing line segment RS.
- Mark the intersection point as X.
- Label the points as follows: P, Q on line PQ and R, S on line RS.
3. Apply the Isosceles Triangle Property:
- Since XP=XR, triangle XPR is isosceles with XP=XR.
- This means that the angles opposite to these equal sides are also equal. Therefore, ∠XPR=∠XRP.
4. Use the Given Angle Condition:
- We know that ∠PSX=∠RQX.
- By the property of angles in a triangle, we can say that if two angles are equal, the sides opposite those angles are also equal.
5. Conclude the Relationship:
- Since ∠PSX=∠RQX and XP=XR, we can conclude that triangle XPS is similar to triangle XQR.
- This leads us to the conclusion that the lengths of the segments PS and QR must also be equal.
6. Final Statement:
- Therefore, we conclude that PS=QR.
Conclusion:
The relationship derived from the given conditions is that PS=QR.
- We have two line segments PQ and RS intersecting at point X.
- The lengths of the segments are equal: XP=XR.
- The angles formed at point X are equal: ∠PSX=∠RQX.
- Draw two intersecting lines, one representing line segment PQ and the other representing line segment RS.
- Mark the intersection point as X.
- Label the points as follows: P, Q on line PQ and R, S on line RS.
- Since XP=XR, triangle XPR is isosceles with XP=XR.
- This means that the angles opposite to these equal sides are also equal. Therefore, ∠XPR=∠XRP.
- We know that ∠PSX=∠RQX.
- By the property of angles in a triangle, we can say that if two angles are equal, the sides opposite those angles are also equal.
- Since ∠PSX=∠RQX and XP=XR, we can conclude that triangle XPS is similar to triangle XQR.
- This leads us to the conclusion that the lengths of the segments PS and QR must also be equal.
- Therefore, we conclude that PS=QR.
The relationship derived from the given conditions is that PS=QR.
Topper's Solved these Questions
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:TRY YOURSELF
Explore 25 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIII)
Explore 70 Videos
- DISCOUNTBook:KIRAN PUBLICATIONChapter:DISCOUNTExercise:Test Yourself
Explore 10 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
Similar Questions
Two line segments may intersect at two points
View SolutionTwo lines PQ and RS cut each other at X such that XP = XR. If ∠PSX=∠RQX then-
View SolutionWhich of the following statements are true and which are false ?
If two line segments do not intersect, they are parallel.
View SolutionSuppose line segments AB and CD intersect at O in such a way that AO=OD and OB=OC. Prove that AC=BD but AC may not be parallel to BD
View SolutionLines PQ and RS intersect each other at point O. If ∠POR:∠ROQ=5:7, find all the angles.
View Solution(i) No two line segments intersect except at their endpoints.
View SolutionIn Figure, two straight lines PQ and RS intersect each other at O. If ∠POT=750, find the values of a,b and c
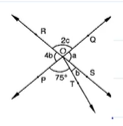
View SolutionTwo non - parallel line segments will always intersect.
View SolutionIn figure, if lines PQ and RS intersect at a point T such that PRT=400,∠RPT=950 and ∠TSQ=750, find ∠SQT.
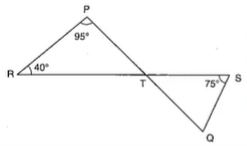
View SolutionPoint A lies on the line segment PQ joining P(6, -6) and Q(-4, -1) in such a way that PAPQ=25. If the point A also lies on the line 3x+k(y+1) = 0, find the value of k.
View Solution
