If D, E and F be the middle points of the sides BC,CA and AB of the ΔABC, then AD+BE+CF is
a zero vector
a unit vector
0
none of these
The correct Answer is:A
AD=OD−OA
=b+c2−a=b+c−2a2 [where, O is the origin for reference]
Similarly, BE=OE−OB=c+a2−b
=c+a−2b2
and CF=a+b−2b2
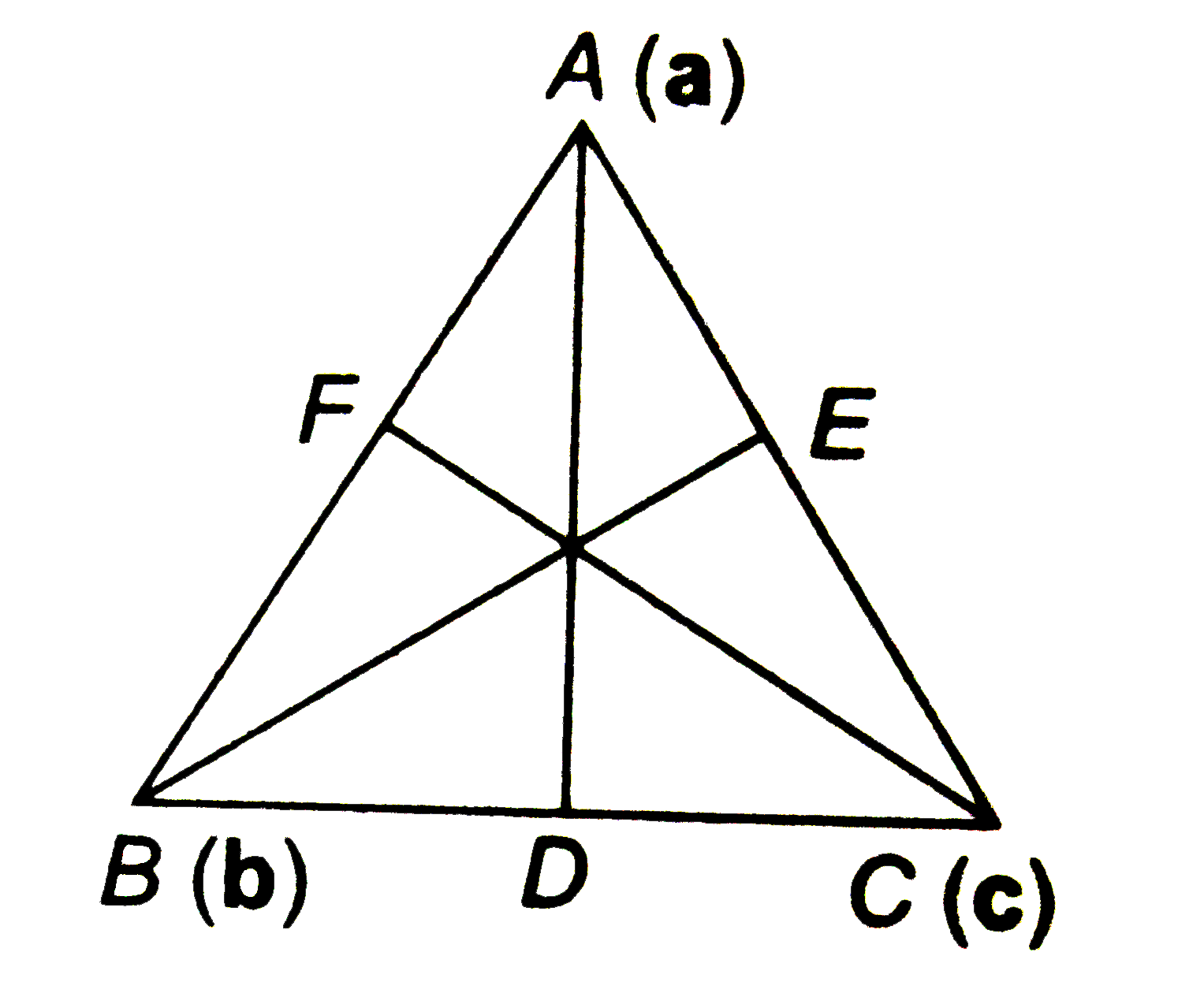
Now, AD+BE+CF=b+c−2a2+c+a−2b2+a+b−2c2=0
Topper's Solved these Questions
- VECTOR ALGEBRABook:ARIHANT MATHSChapter:VECTOR ALGEBRAExercise:Exercise (More Than One Correct Option Type Questions)
Explore 7 Videos
- VECTOR ALGEBRABook:ARIHANT MATHSChapter:VECTOR ALGEBRAExercise:Exercise (Statement I And Ii Type Questions)
Explore 3 Videos
- VECTOR ALGEBRABook:ARIHANT MATHSChapter:VECTOR ALGEBRAExercise:Exercise For Session 3
Explore 11 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBook:ARIHANT MATHSChapter:TRIGONOMETRIC FUNCTIONS AND IDENTITIESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 19 Videos
Similar Questions
Knowledge Check
Let D, E and F be the middle points of the sides BC,CA and AB respectively of a triangle ABC. Then, AD + BE + CF equals to
A0B0C2DNone of theseIf D,E and F are the mid-points of the sides BC,CA and AB, respectively of a ΔABC and O is any point, show that
(i) AD+BE+CF=0
(ii) OE+OF+DO=OAAA. a zero vectorBB. a unit vectorCC. 0DD. none of theseIn the given figure, D, E and F are the midpoints of the sides BC, CA and AB of ΔABC.BE bisect DF at X while CF bisect DE at Y, then BC = a XY. Find a.
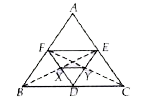 A3B4C2D1/4
A3B4C2D1/4
Let D,EandF be the middle points of the sides BC,CAandAB, respectively of a triangle ABC. Then prove that →AD+→BE+→CF=→0 .
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB of the equilateral ΔABC. Prove that ΔDEF is also an equilateral triangle.

View SolutionD, E and F are the mid-points of the sides BC, CA and AB of a triangle ABC. Show that
BDEF is a parallelogram
View SolutionIf D,E,andF are three points on the sides BC,AC,andAB of a triangle ABC such that AD,BE,andCF are concurrent, then show that BD⋅CE⋅AF=DC⋅EA⋅FB .
View SolutionIf D, E and F are respectively the mid - points of sides BC, AC and AB of a ΔABC. If EF=3cm,FD=4cm and AB=10cm, then DE,BCandCA respectively will be equal to :
View Solution

