E and F are the mid-points of the sides AB and CD of a parallelogram ABCD. Prove that the line segment AF and CE trisects BD in three equal parts.
ABCD is a parallelogram
is a parallelogram

In
F is the mid-point of DC
and
N is the mid-point of DM.
In
E is the mid-point of AB.
M is the mid-point of BN.
From eqs, (1) and (2)
AF and CE, divides the diagonal BD into three equal parts.
Topper's Solved these Questions
- QUADRILATERALSBook:NAGEEN PRAKASHANChapter:QUADRILATERALSExercise:Problems From NCERT/exemplar
Explore 11 Videos
- QUADRILATERALSBook:NAGEEN PRAKASHANChapter:QUADRILATERALSExercise:Exercise 8a
Explore 29 Videos
- PROBABILITYBook:NAGEEN PRAKASHANChapter:PROBABILITYExercise:Revision Exercise (very Short Answer /short Answer Questions)
Explore 10 Videos
- STATISTICSBook:NAGEEN PRAKASHANChapter:STATISTICSExercise:Revision Exercise
Explore 10 Videos
Similar Questions
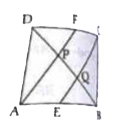
In Figure, ABCD is a parallelogram. E and F are the mid-points of the sides AB and CD respectively. Prove that the line segments AF and CE triset (divide into three equal parts) the diagonal BD.

View SolutionIn Figure, ABCD is a parallelogram. E and F are the mid-points of the sides AB and CD respectively. Prove that the line segments AF and CE trisect (divide into three equal parts) the diagonal BD .
View Solution
Knowledge Check
Points E and F are respectively midpoints of sides AB and CD of a rectangle ABCD. If line segment AF and EC respectively intersect diagonal BD at P and Q, then what is the length of PQ if sides of rectangle are respectively 10 cm and 24 cm ?
A10 cmB17 cmC323 cmD263 cmIn the given figure, M is the mid-point of the side CD of the parallelogram ABCD. What is ON:OB?
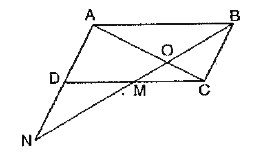 A3:2B2:1C3:1D5:2
A3:2B2:1C3:1D5:2
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively. Show that the line segments AF and EC trisect the diagonal BD.

View SolutionIf P and Q are the mid points of the sides AB and CD of a parallelogram ABCD, prove that DP and BQ cut the diagonal AC in its points of trisection which are also the points of trisection of DP and BQ respectively.
View SolutionIn a parallelogram ABCD, points E and F are respectively midpoint of sides AB and CD (see the adjacent figure). Prove that line segment AF and EC trisect diagonal BD.
View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides BC and AD respectively. Show that the line segment BF and ED trisect the diagonal AC.
View SolutionThe sides AB and CD of a parallelogram ABCD are bisected at EandF . Prove that EBFD is a parallelogram.
View SolutionThe middle points of the parallel sides AB and CD of a parallelogram ABCD are P and Q respectively. If AQ and CP divide the diagonal BD into three parts BX, XY and YD, then which one of the following is correct ?
View Solution