A leakage begins in water tank at position P as shown in the figure. The initial gauge pressure pressure above that of the atmosphere at P was 5 x 105 N/m2. If the density of water is 1000 kg/m3 the initial velocity with which water gushes out is a 3.2 m/sb 32 m/sc 28 m/sd 2.8 m/s
Correct option b 32 m/sExplanation :
Related Solutions
A leakage begins in water tank at position P as shown in the figure. The gauge pressure (pressure above that of the atmosphere) at P was . If the density of water is the initial velocity with which water gushes out is approximately
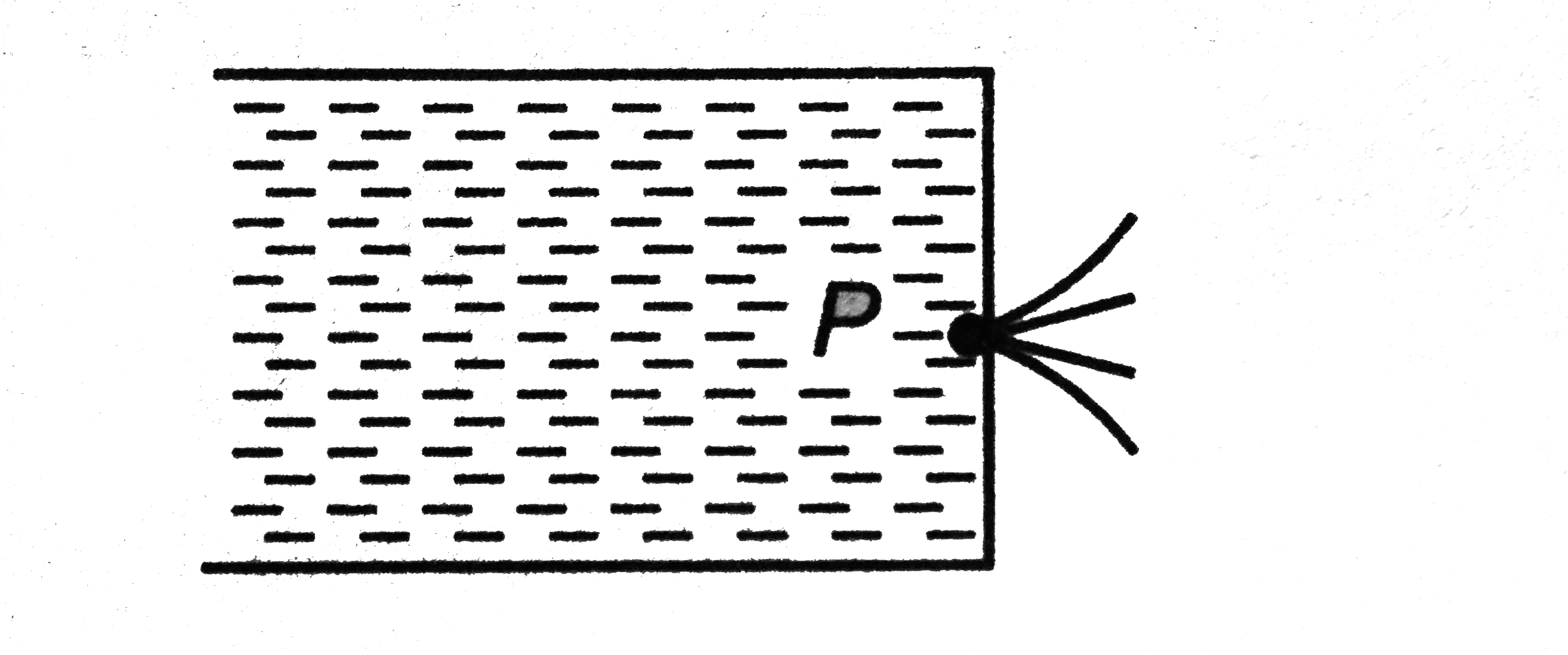
View SolutionA leakage begins in water tank at position P as shown in the figure. The gauge pressure (pressure above that of the atmosphere) at P was 5xx10^(5) N//m^(2) . If the density of water is 1000kg//m^(3) the initial velocity with which water gushes out is approximately
View SolutionWith what velocity does water flow out of an orifice in a tank with gauge pressure before the flow starts? Density of water .
View SolutionIf the water emerge from an orifice in a tank in which the gauge pressure is before the flow starts, then what will be the velocity of the water emerging out ? Take density of water is
View SolutionIf the water emerge from an orifice in a tank in which the gauge pressure is 4xx10^(5) Nm^(-2) before the flow starts, then what will be the velocity of the water emerging out ? Take density of water is 1000 kg m^(-3)
View Solutionwater (density = 1000 kg//m^(3) A hole is made at the bottom of a tank filled with If the excess pressure at the bottom of the tank is three atmospheres (1 atmosphere =10^(5)N//m^(2) ), then the outflow velocity is
View SolutionWith what velocity does water flow out of an orifice in a tank with gauge pressure before the flow starts? Density of water=
View SolutionAt What velocity does water emerge from an orifice in a tank in which gauge pressure is 3 xx 10^(5) Nm^(-2) before the flow starts ? (Take the density of water =1000 kg m^(-3) .)
View SolutionAt What velocity does water emerge from an orifice in a tank in which gauge pressure is 3 xx 10^(5) Nm^(-2) before the flow starts ? (Take the density of water =1000 kg m^(-3) .)
View SolutionA tank with length 10 m. breadth 8 m and depth 6 m is filled with water upto top . If . And density of water , then the thrust on the bottom is:
View SolutionAssertion : Water is flowing through a horizontal tube, the static pressure and total pressure at any point are P and P . If the density of water is , the velocity of liquid flow is 4 m/s.
Reason : Work done on the liquid by difference in pressure is equal to gain in K.E. of liquid
View SolutionIf the gauge pressure, at the bottom of a water tank is 2.7 kPa, what is the height of the water [Take g = 10 m ]
Hint : Gauge Pressure = absolute pressure - atmospheric pressure = pgh
View SolutionIf the gauge pressure, at the bottom of a water tank is 2.7 kPa, what is the height of the water [Take g = 10 m ]
Hint : Gauge Pressure = absolute pressure - atmospheric pressure = pgh
View SolutionWhat is the pressure in an ocean at a depth of 1000 m, if the density of water is . Atmospheric pressure Pa.
View SolutionA swimmer is swimming in a swimming pool at 6 m below the surface of the water. Calculate the pressure on the swimmer due to water above. (Density of water )
View SolutionA water tank is deep .If the water barometer reads at that place, then what is the pressure at the bottom of the tank in atmosphere?
View SolutionA water tank is 20 m deep . If the water barometer reads 10 m at the surface , then what is the pressure at the bottom of the tank in atmosphere ?
View SolutionA water tank is 20 m deep . If the water barometer reads 10 m at the surface , then what is the pressure at the bottom of the tank in atmosphere ?
View Solutionजल में ध्वनि का वेग 1400 मी/से है, जल का घनत्व 1000 किग्रा/मी है, आयतन प्रत्यास्थता गुणांक है
View SolutionAn open rectangular tank of dimensions 6mxx5mxx4m contains water upto height of 2m. The vessel is accelerated horizontally with an acceleration of a m//s^(2) as shown. Take rho_("water")=10^(3)kg//m^(3) g=10m//s^(2) atmospheric pressure =10^(5)N//m^(2) . Bese on above information answer the following questions: Instead of open top if the vessel is closed then absolute pressure at point A would be [take a=(20)/(3)m//s^(2) and initially height of water in tank is 2m]
View Solution