Assertion : Water is flowing through a horizontal tube, the static pressure and total pressure at any point are $1.20 \times 10^{5}$ P and $1.28 \times 10^{5}$ P . If the density of water is $1000 k g / m^{3}$ , the velocity of liquid flow is 4 m/s.
Reason : Work done on the liquid by difference in pressure is equal to gain in K.E. of liquid

both Assertion and Reason are true and the Reason in the correct explanation of the Assertion.

both Assertion and Reason are true but Reason is not a correct explanation of the Assertion.

Assertion is true but the Reason is false.

both Assertion and Reason are false.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

A leakage begins in water tank at position P as shown in the figure. The gauge pressure (pressure above that of the atmosphere) at P was $5 \times 10^{5} N / m^{2}$ . If the density of water is $1000 k g / m^{3}$ the initial velocity with which water gushes out is approximately

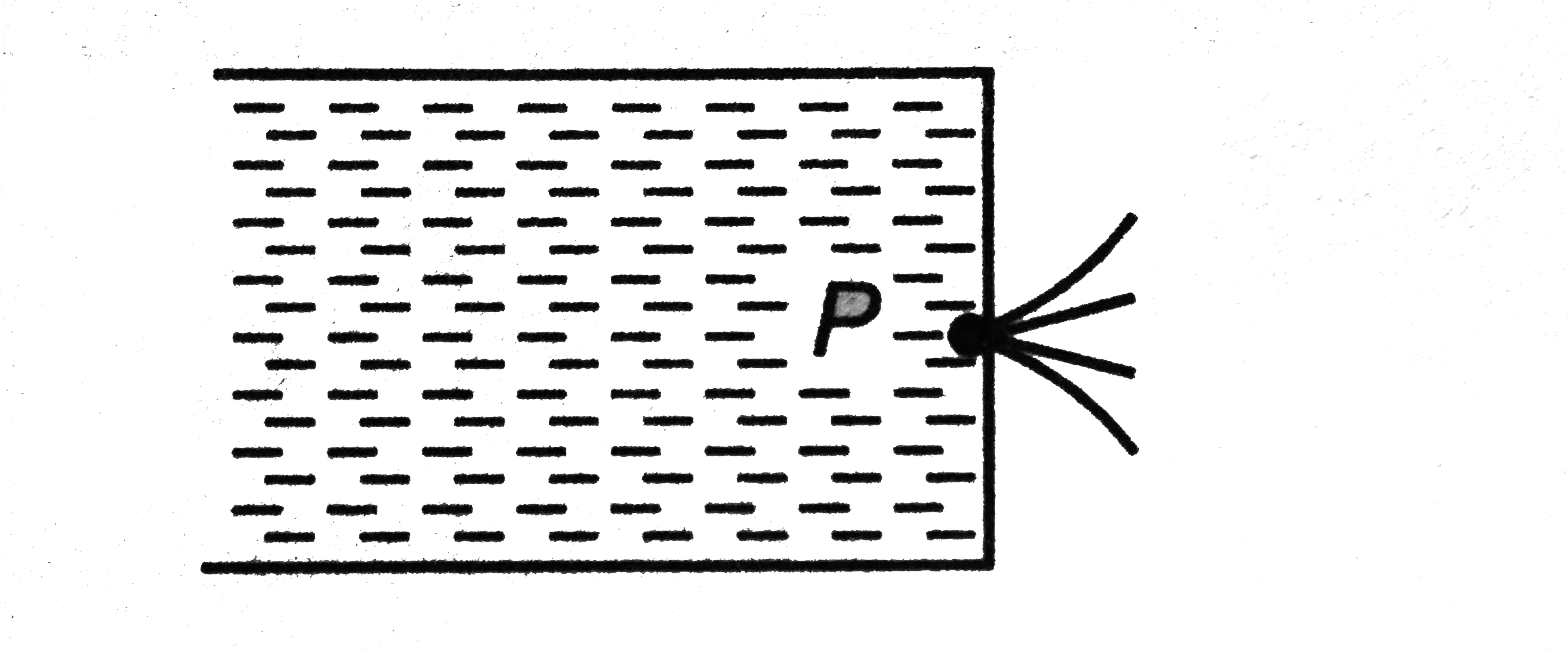A $3.2 m s^{- 1}$
B $32 m s^{- 1}$
C $28 m s^{- 1}$
D $2.8 m s^{- 1}$
Water is flowing streamline motion through a horizontal tube. The pressure at a point in a tube is P where the velocity of flow is v. At another point where the pressure is $\frac{p}{2}$ , the velocity of flow is (density of water = $ρ$ )
A $\sqrt{} v^{2} + \frac{p}{ρ}$
B $\sqrt{} v^{2} - \frac{p}{ρ}$
C $\sqrt{} v^{2} + \frac{2 p}{ρ}$
D $\sqrt{} v^{2} - \frac{2 p}{ρ}$
Water is flowing through a horizontal tube. The pressure of the liquid in the portion where velocity is $2 m / s$ is 2 m of Hg. What will be the pressure in the portion where velocity is $4 m / s$
A $2.66 \times 10^{5} P a$
B $2.78 \times 10^{5} P a$
C $2.84 \times 10^{5} P a$
D $2.60 \times 10^{5} P a$